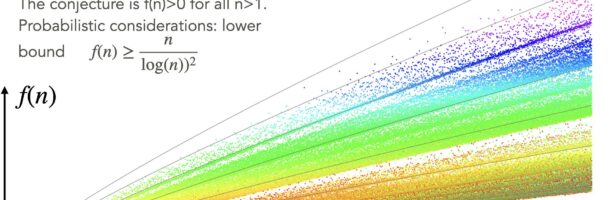
Goldbach has been hugely popular recently. It appeared in movies, and books. on some major youtube math sites like numberphile or veritasium recently. That show featured also Harald Helfgott, who had shown the ternary conjecture more than a decade ago. The conjecture is probably the most popular math problem of all. It is part of the 4 Landau problems which I made in 2018 a poem about at the occasion of a math table talk of 2018 about the Goldbach comet. (See the slides[PDF] and the handout). The veritasium story takes a bit of an original approach in bracketing the story about Jingrun Chen who worked seriously on the problem. [Just a soft critique I find it remarkable how political correctness forbids current youtubers to mention Russian mathematicians like Ivan Vinogradov who made contributions which are comparable with Chen’s work. But one can understand: social media folks have to push the right buttons in order to be successful. Apropos Chinese mathematicians: my personal “number theory bible” in college had been the fantastic book of Hua Loo Keng : “Introduction to Number Theory” from 1982) (which I still consider one of the best and clearest written number theory books out there). I had tried in high school to read Vinogradov’s book but did not manage to understand much. The work of J.R. Chen is mentioned in the textbook of Hua Loo Keng several times, so that maybe also the veritasium approach to the theme is not that original. The presentation of Derek Muller however is absolutely fantastic and especially good is that some expert (Helfgott) appears. Below is a presentation from 2022 from a course on the history of mathematics courses taught at the extension school. I also talked about Goldbach in a linear algebra course of 2022. (See this lecture [PDF] where it was part of the proof canon in that course. (math 22b was then still linear algebra). I documented a bit on this page from 2007 “Encounters with Goldbach” about my early obsession with Goldbach. It had been written 2007, at the 300th birthday of Leonard Euler. –[Unfortunately, as a few years ago, our server abel in the math department had changed, and google lost most links from personal websites and has the old server URL. Google has lost much of its ability to re-index websites. That had been better 25 years ago when google started. The spiders had been able to keep relevant links up to date and to note that abel.math.harvard.edu has become people.math.harvard.edu] So, here is again the link about Encounters with Goldbach ….just as a hint to google to pick it up. And for me to connect more dots: I worked in June 2016 on Goldbach conjectures for Gaussian, Hurwitz, Octavian and Eistenstein primes (ArXiv), which had been part of a burst on experiments in number theory. My own Gaussian Goldbach conjecture is that every even Gaussian integer a+ib with a>1,b>1 is the sum of two Gaussian primes and that every Eisenstein integer (a,b) with a>3, b>3 is the sum of two Eisenstein primes. Also catchy is the Quaternion version: every integer quaternion with entries larger than 2 is the sum of two quaternion primes (a,b,c,d) with positive a,b,c,d.
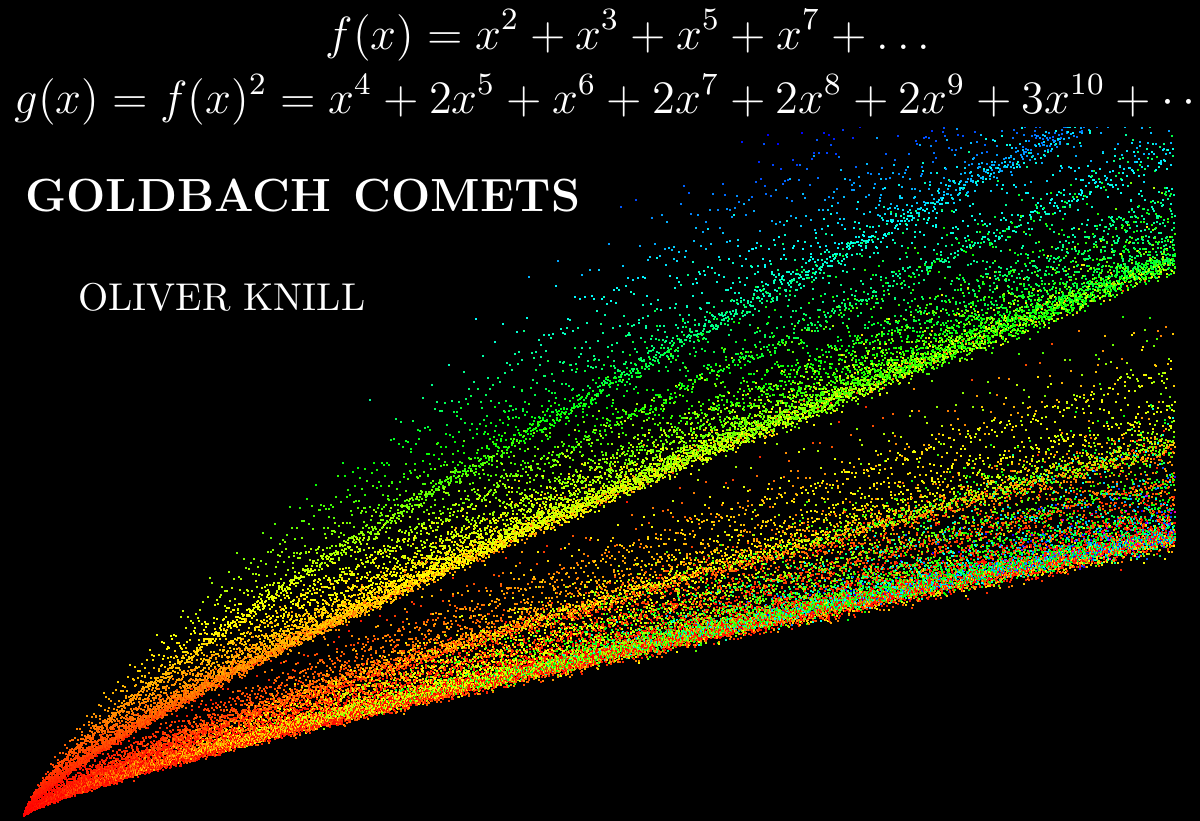
----------------------------------------
The Landau problems
----------------------------------------
Goldbach: Every integer 2n>2
is a sum
of two primes.
Twin prime: There are infinitely
many primes p,
p+2, prime twins.
Legendre: Between two consecutive
perfect squares, there
is a prime.
Landau: There are infinitely
many primes of
the form n^2+1.
----------------------------------------