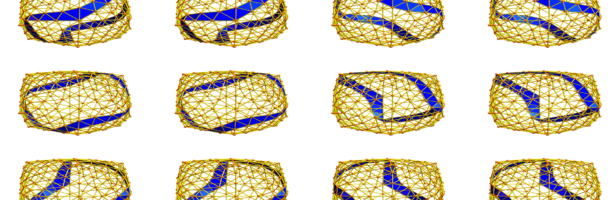
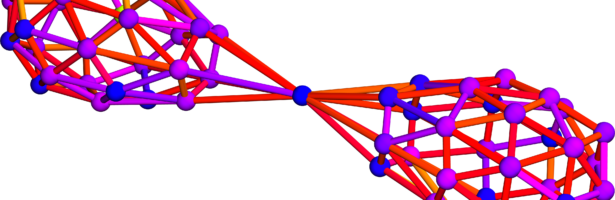
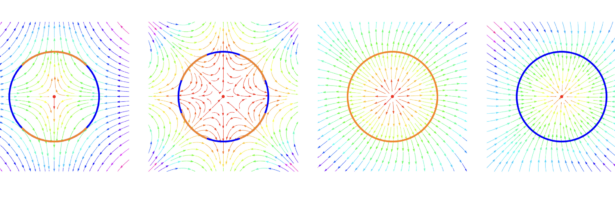
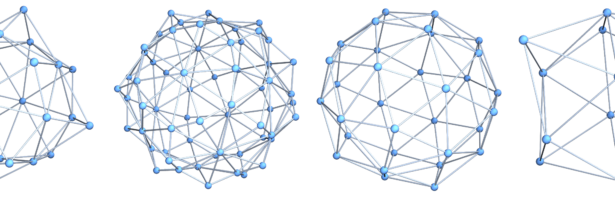
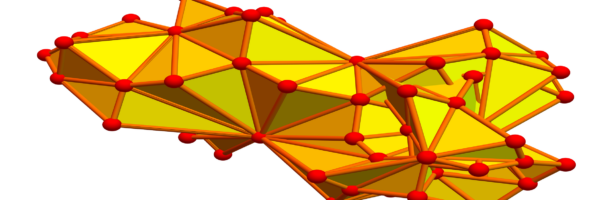
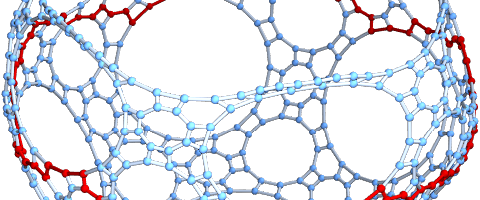
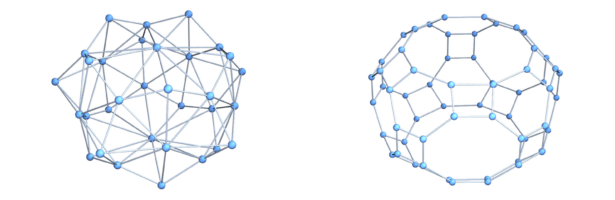
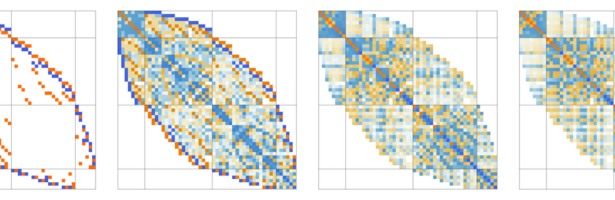
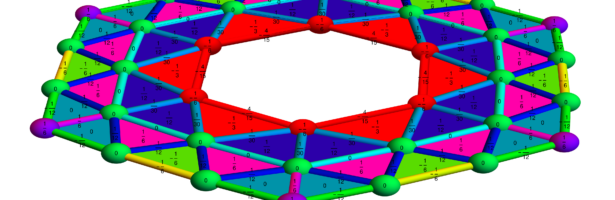
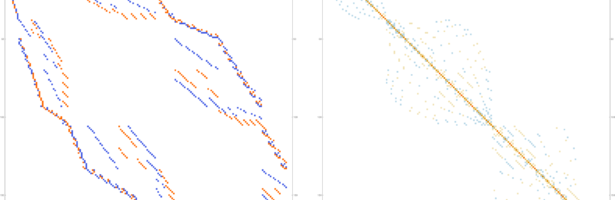
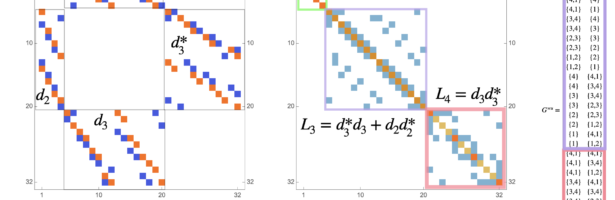
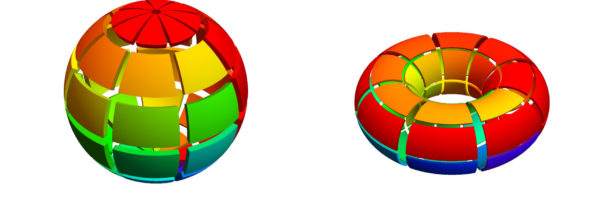
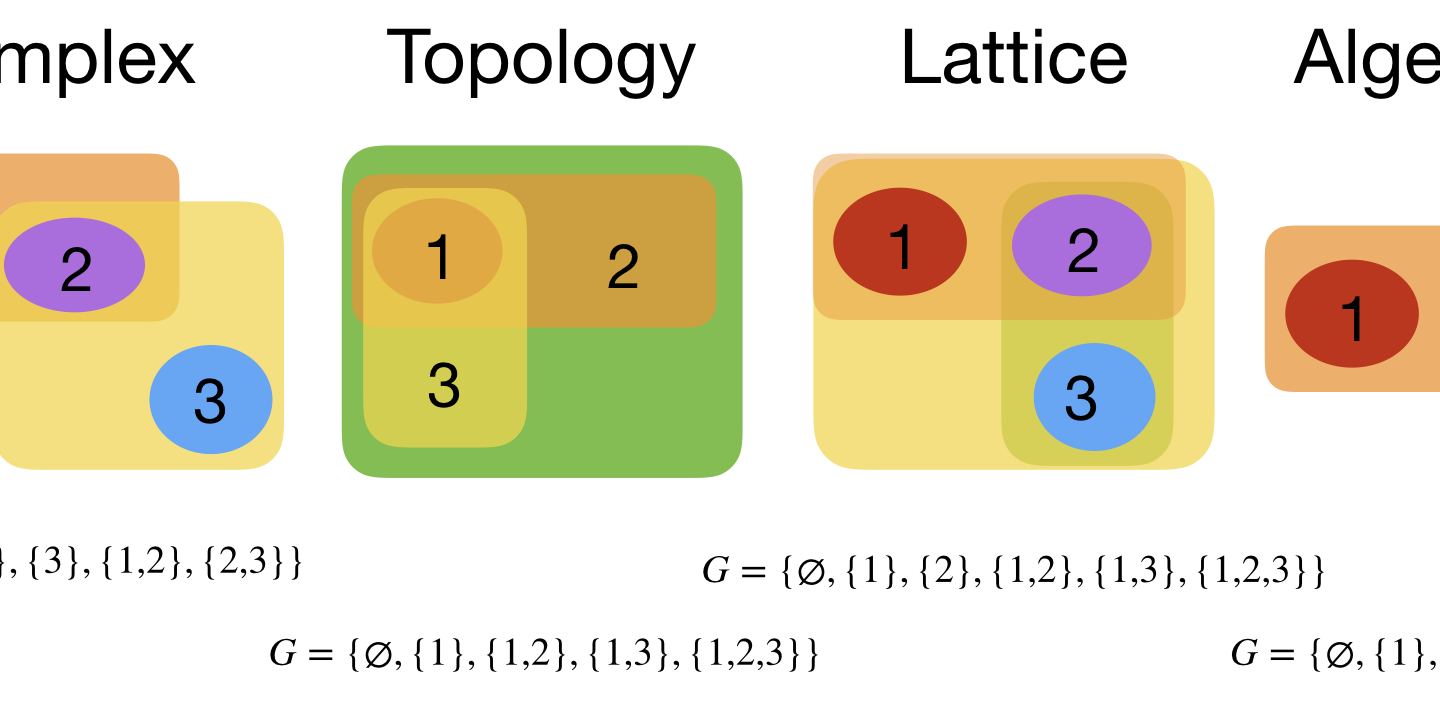
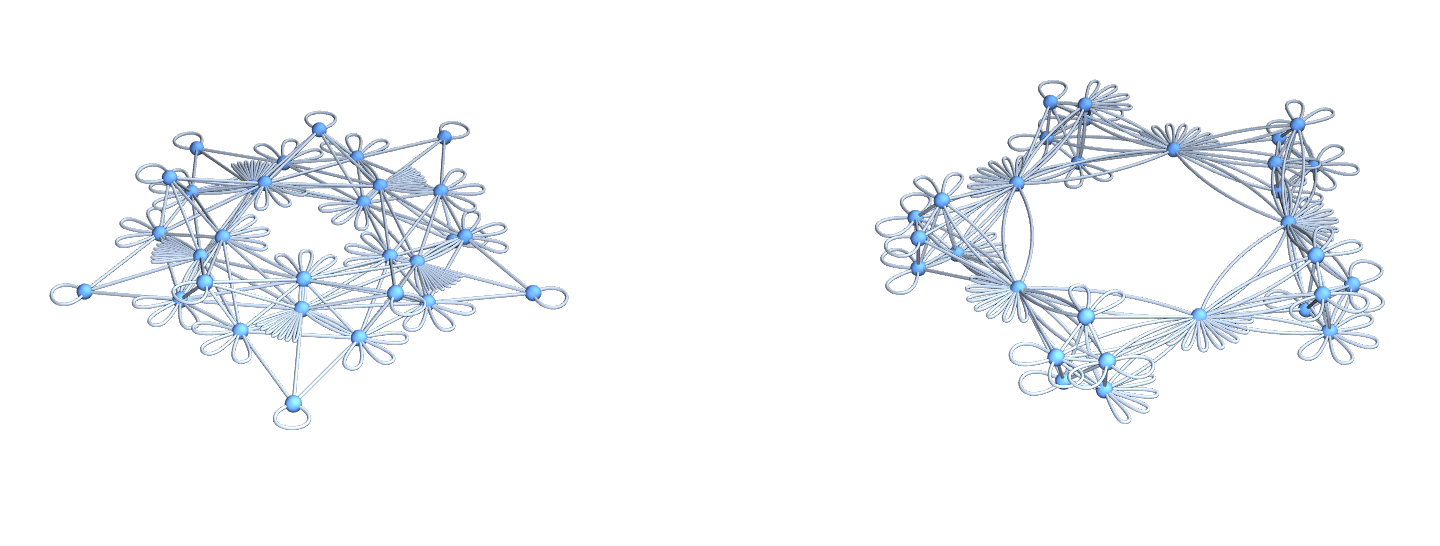
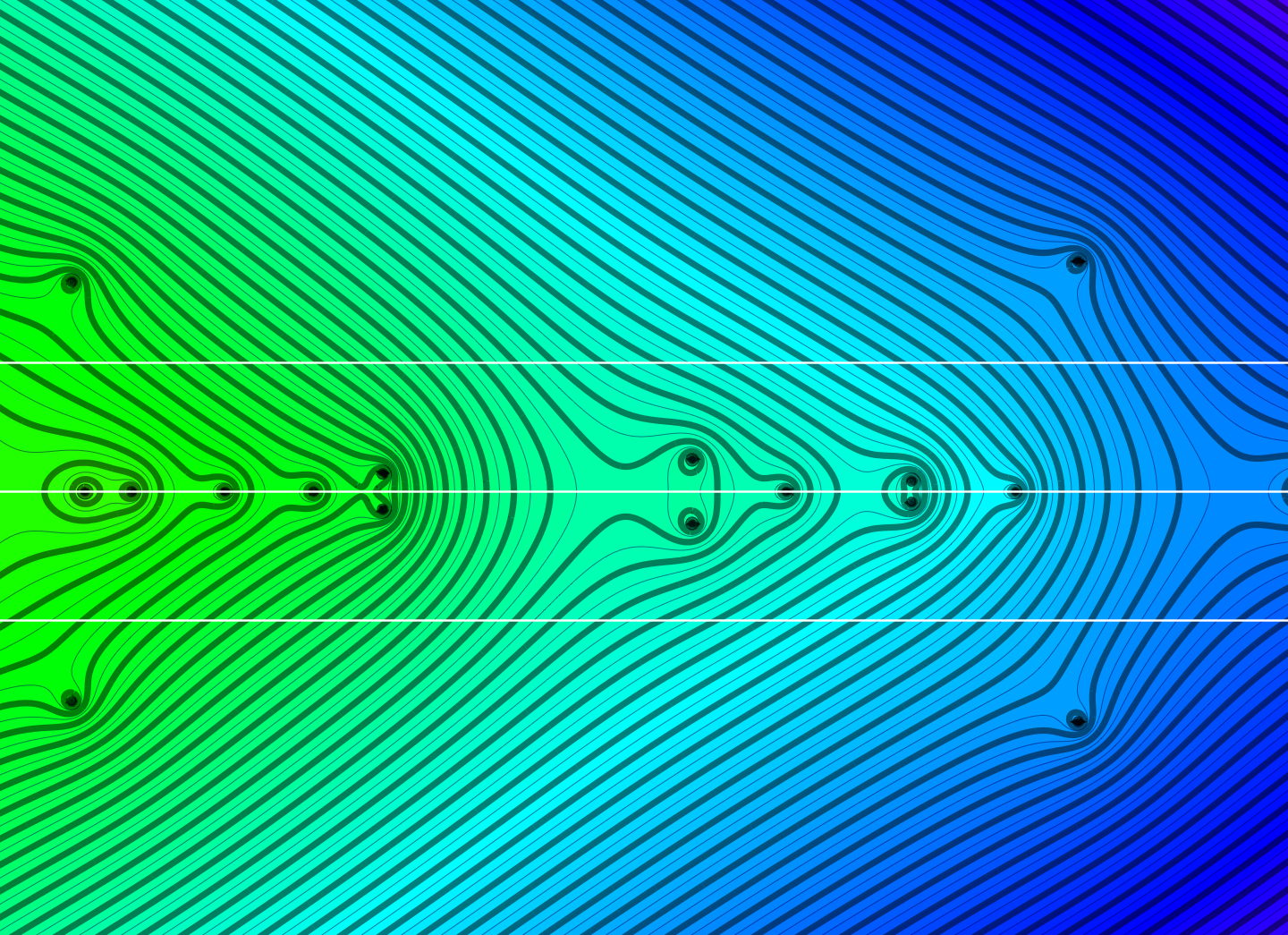
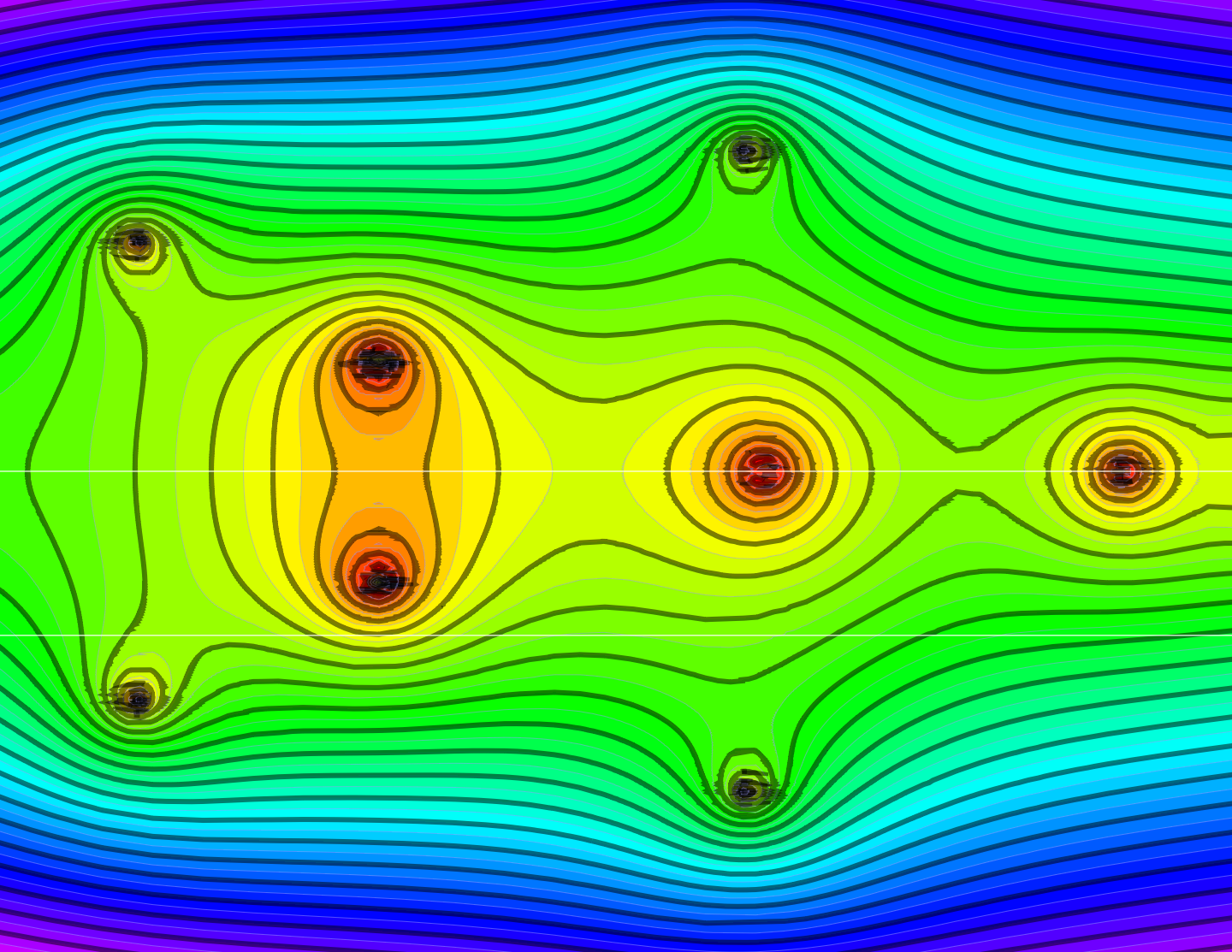
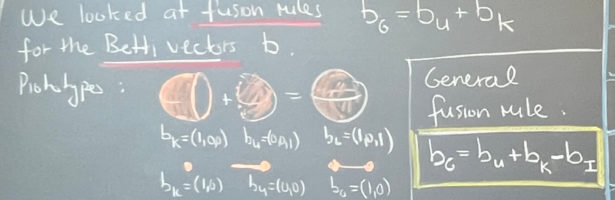Circle Bundles
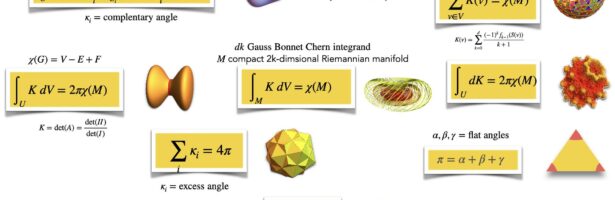
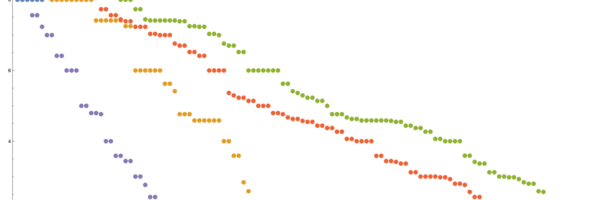
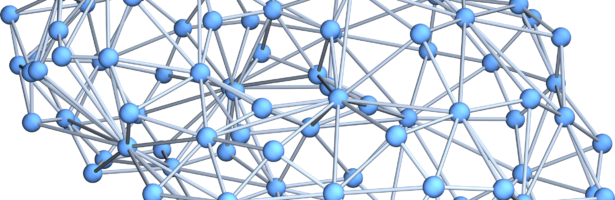
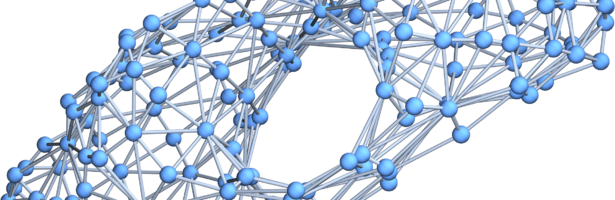
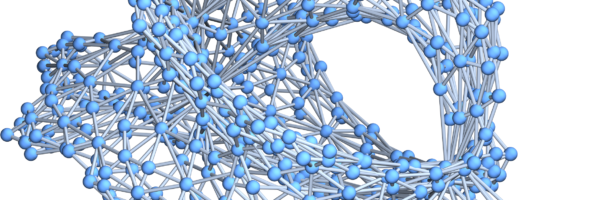
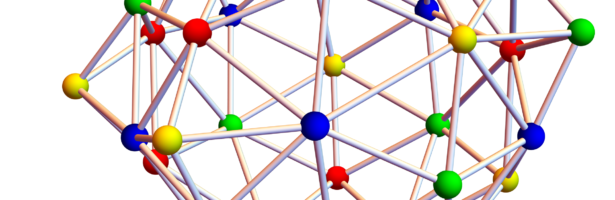
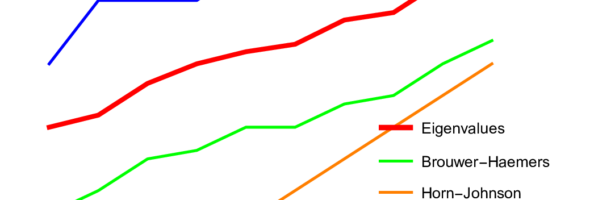
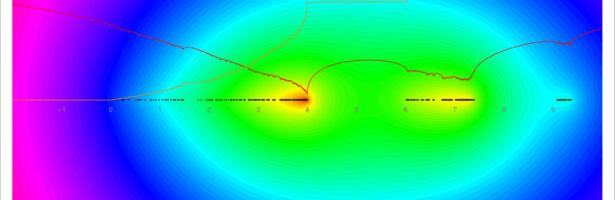
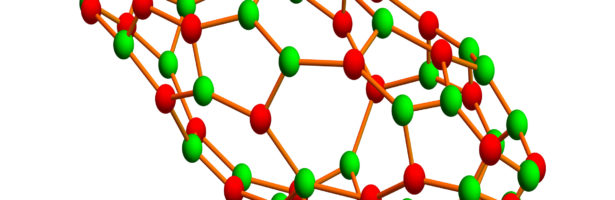
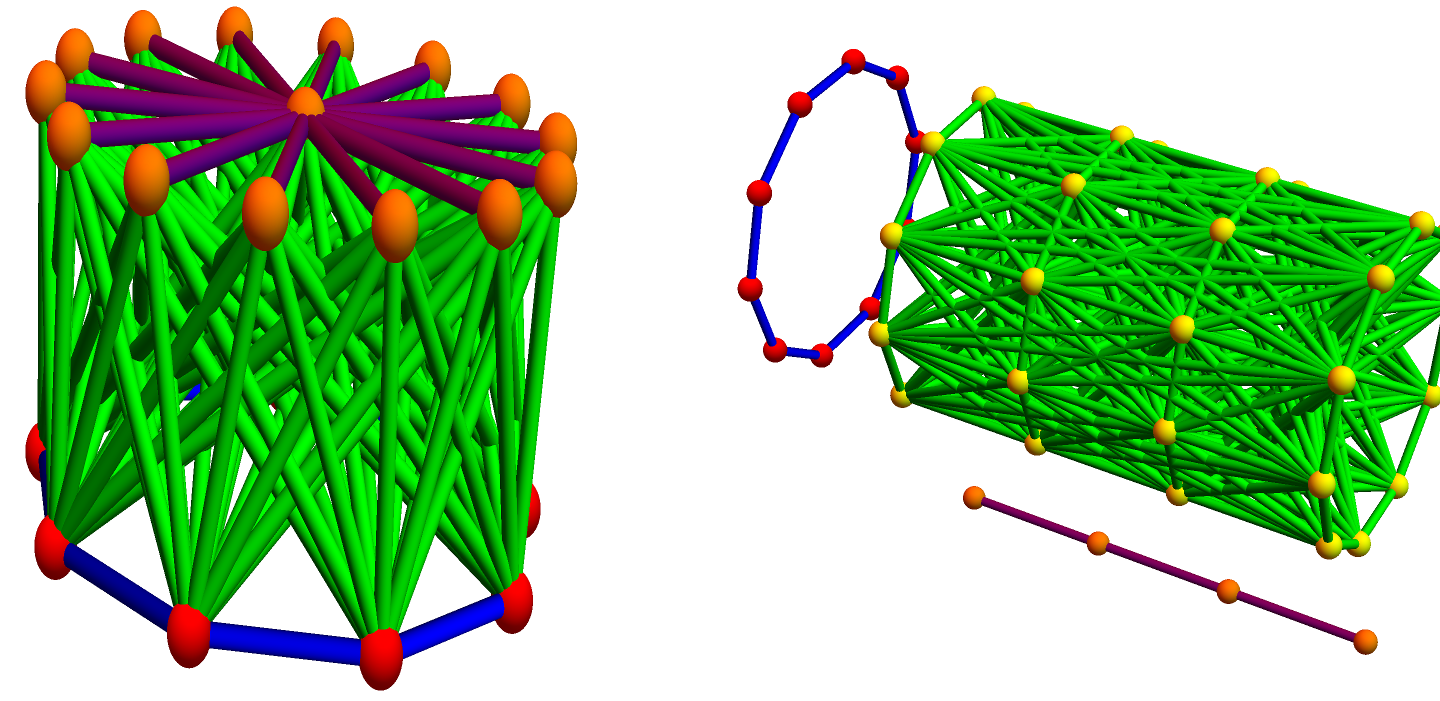
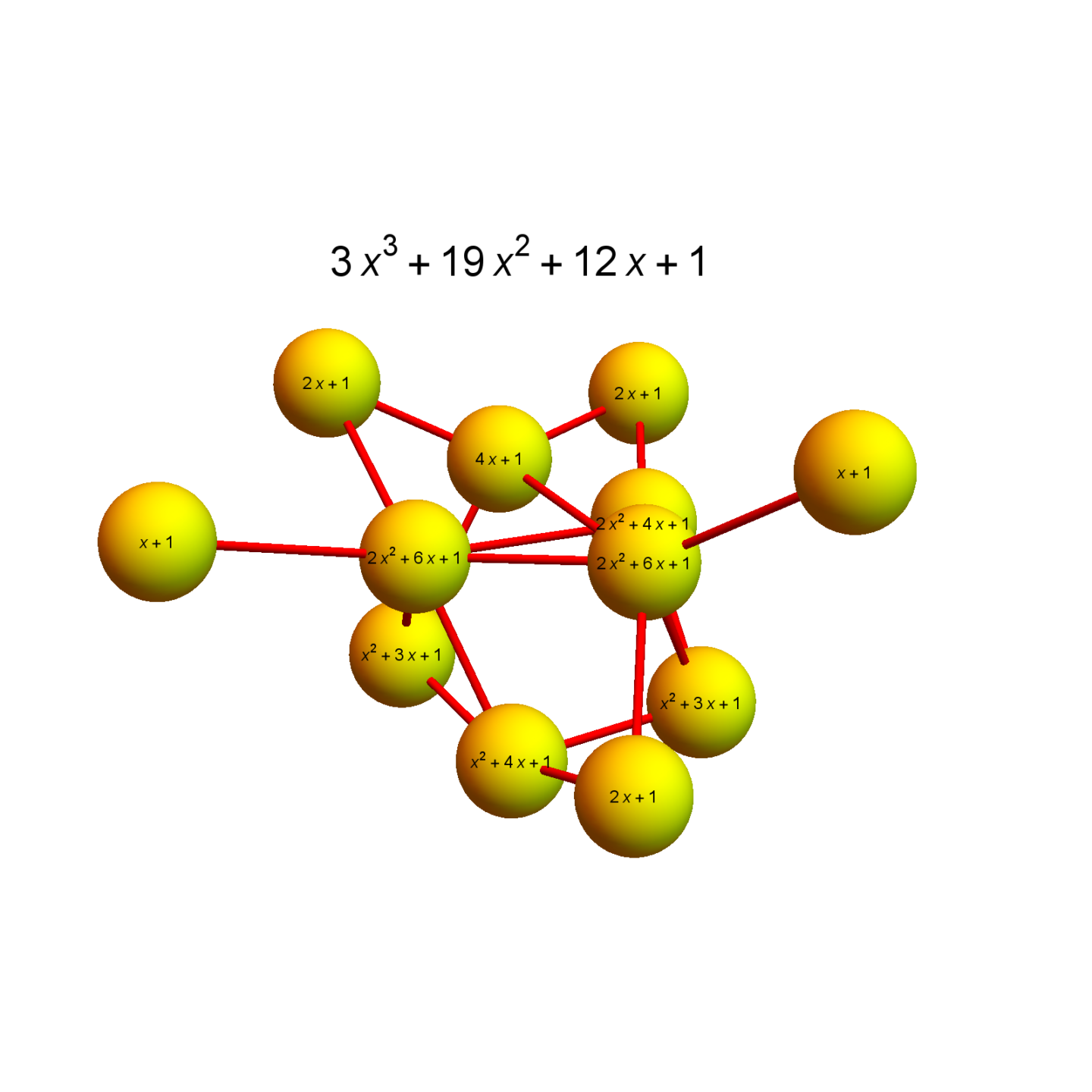
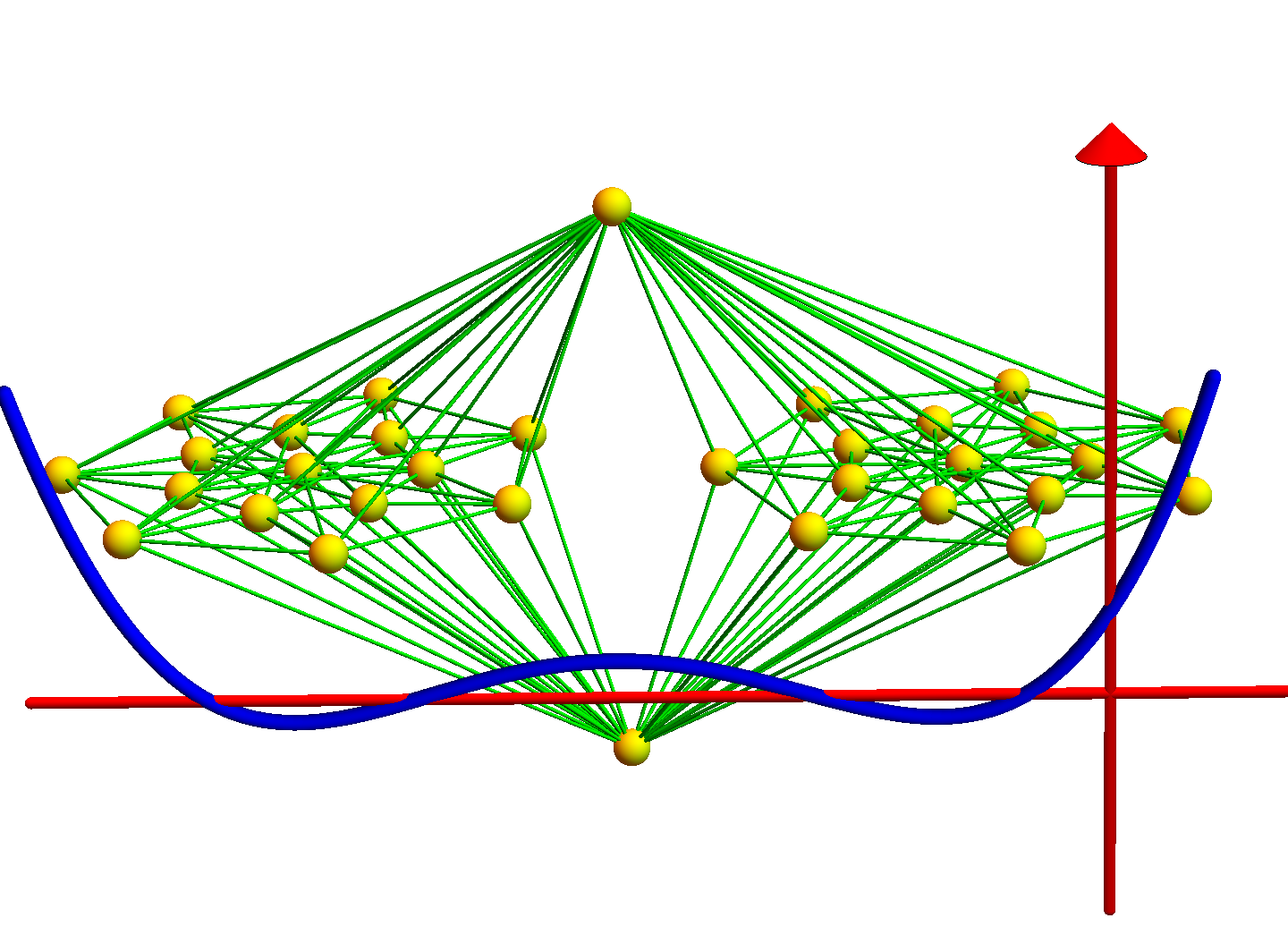
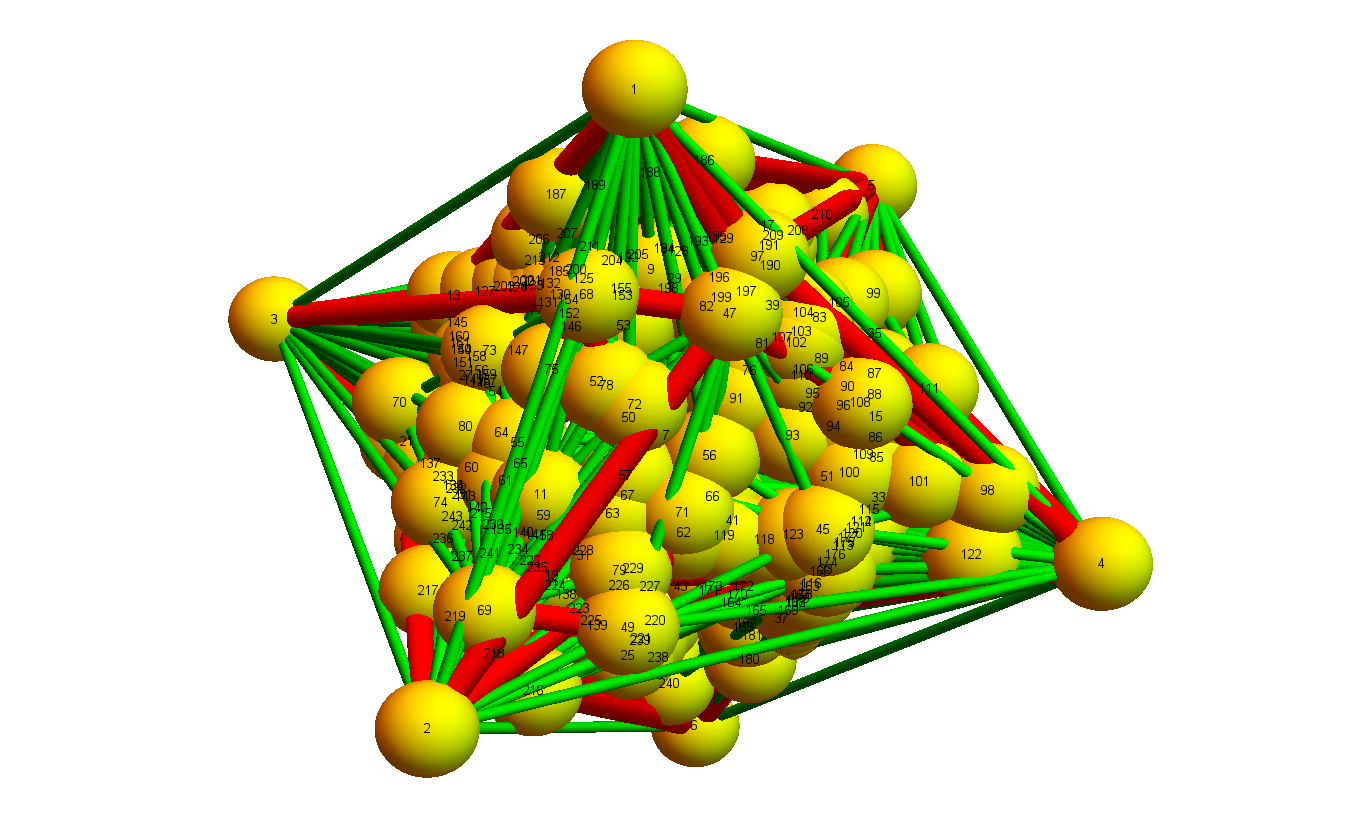
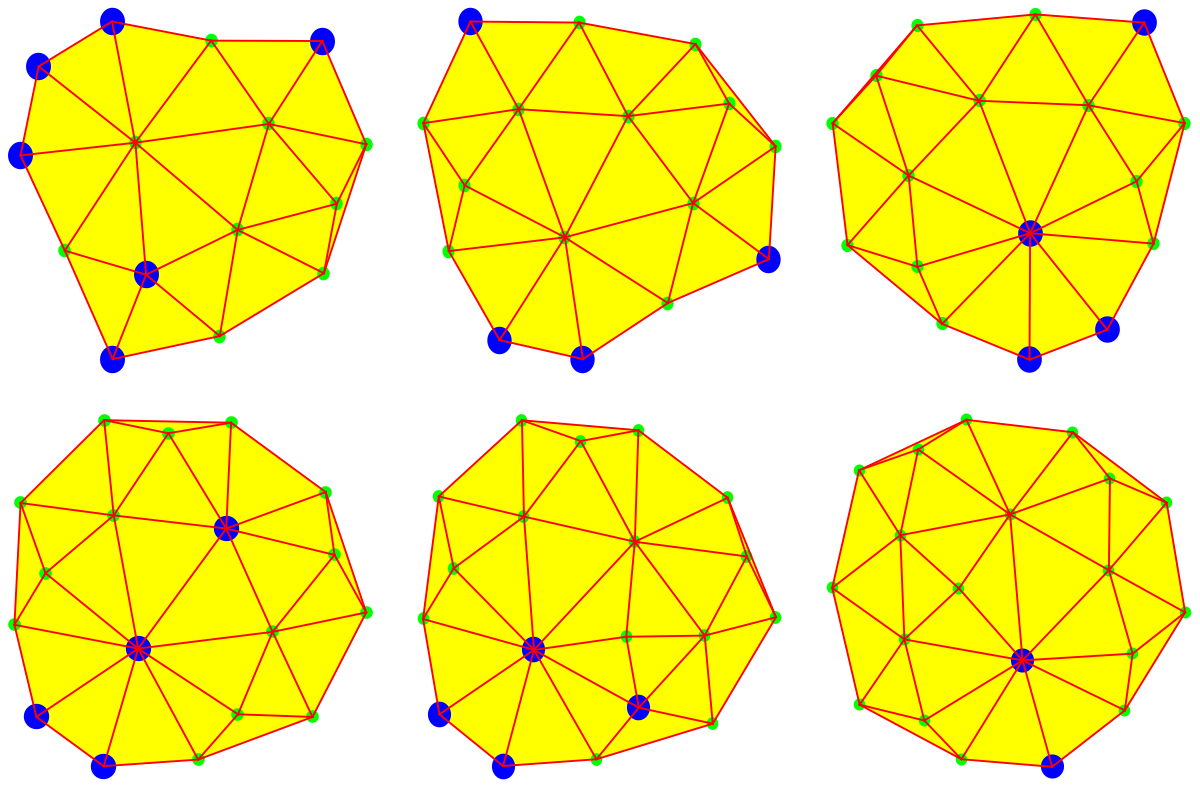
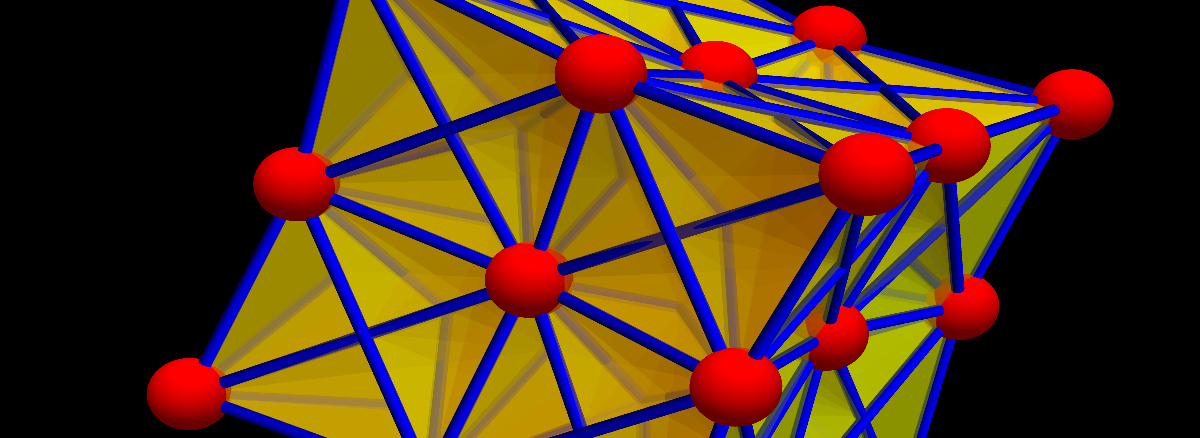
A closed geodesic in a q-manifold is a q-manifold C with boundary dC. This boundary dC is a circle bundle. It can be for example. But it can also be a non-trivial bundle. Note that everything is purely combinatorial and pretty small. For the Moebius strip for example C is …