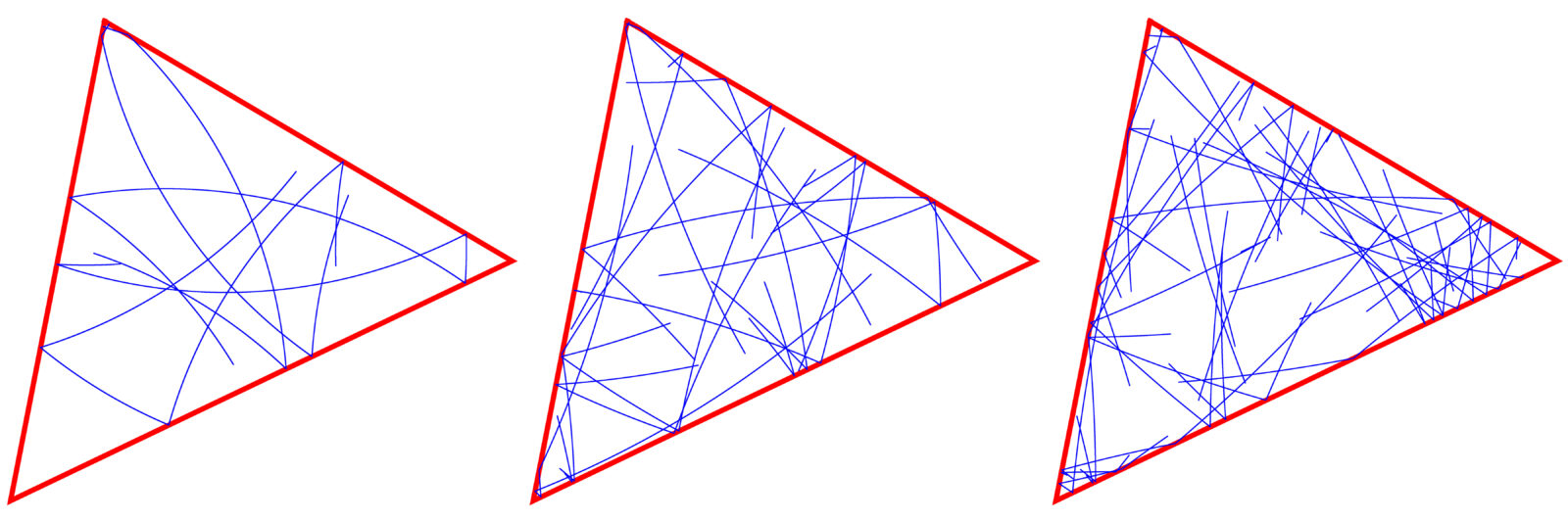
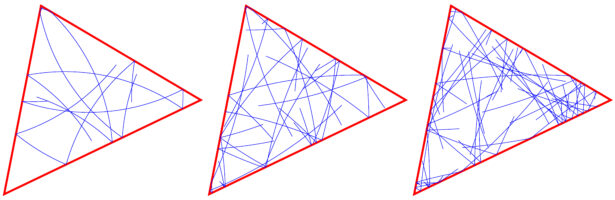
We currently make some more experiments for the density of wave fronts project. We conjecture there for example that for any polygon wave fronts become dense. In cases like eqilateral triangles or right angle triangles this can be proven because doubling produces a parallelogram that tessellates the plane. This is a Veech case where an adaptation of the proof given in our paper works. For a general triangle, the density of wave fronts becomes more likely due to the additional complexity of the flow but paradoxically, we have then less control about the wave front. For a polygon there are some obvious observations: the Lyapunov exponent is zero, the length of the wave front 
