Elements of Finite Geometry - Quantum Calculus

While thinking about some fundamental parts in the story of Dehn-Sommerville, I decided to make a bit of an exercise in imagining how Euclid would have done finite geometry. The result is given in the movie below. Euclid’s elements is undoubtedly one of the milestones in the whole of mathematics and science as it is a shift to rigorous thinking. From today’s perspective, the work of course is defective as even the most basic definitions are ambiguous. Take Definition 1 in book 1 for example: “A point is that which has no part”. Today we cringe about its vagueness: Take the world G={{1,2},{2,3},{1},{1,2,3}} for example. In that space, {2,3},{1} are the points as they have no part and should therefore be called points. But Euclid had a tough assignment. The real line was not constructed yet, the Cartesian product was not available, no set theory, no algebraic tools were at his disposal. It is almost miraculous how much progress are in Euclid’s elements 2300 years ago. Today, one can objectively argue whether a geometry of finite sets is not simpler. It does not go into the difficulty to construct the real line already. It does not go into the difficulty to deal with infinity and essentially all the perils which come from a strong axiom system It is not a replacement of planar geometry of course. Here are my top 10 theorems in planar geometry. Most do not have even remote analogues in the finite (the projective geometry over finite fields comes closest), and some number theory (also covered by Euclid) covers some finite geometry in essence like Babylonian triples which relate to Pythagoras.

I mention in the presentation as proposition 6 the statement that $w_m(B(x))=w_m(U(x)) -(-1)^m w_m(S(x))$ . Let me illustrate this (motivated by Byrne’s attempt to visualize Euclid) in one of the simplest examples, just to appreciate it. The statement is surprisingly deep. For m=1, it follows from the fact that Euler characteristic $w_1(A)$ is a valuation and that the unit ball is the disjoint union of U(x) and S(x). If x is a maximal element in G, meaning that $U(x)=\{x\}$ , then $w_m(U(x))=(-1)^{qm}$ and $w_m(B(x))=(-1)^m$ and $w_m(S(x))=w_1(S(x))=1-(-1)^q$ , the reason being that in that case $B(x))$ is a topological q-ball and $S(x))$ is a topological (q-1)-sphere for which all characteristics agree. Just to appreciate how tricky this Proposition 6 is already, lets look at the complex G={{1},{2},{3},{1,2},{2,3}} generated by F={{1,2},{2,3}}. It is B({2}) for the point {2}. 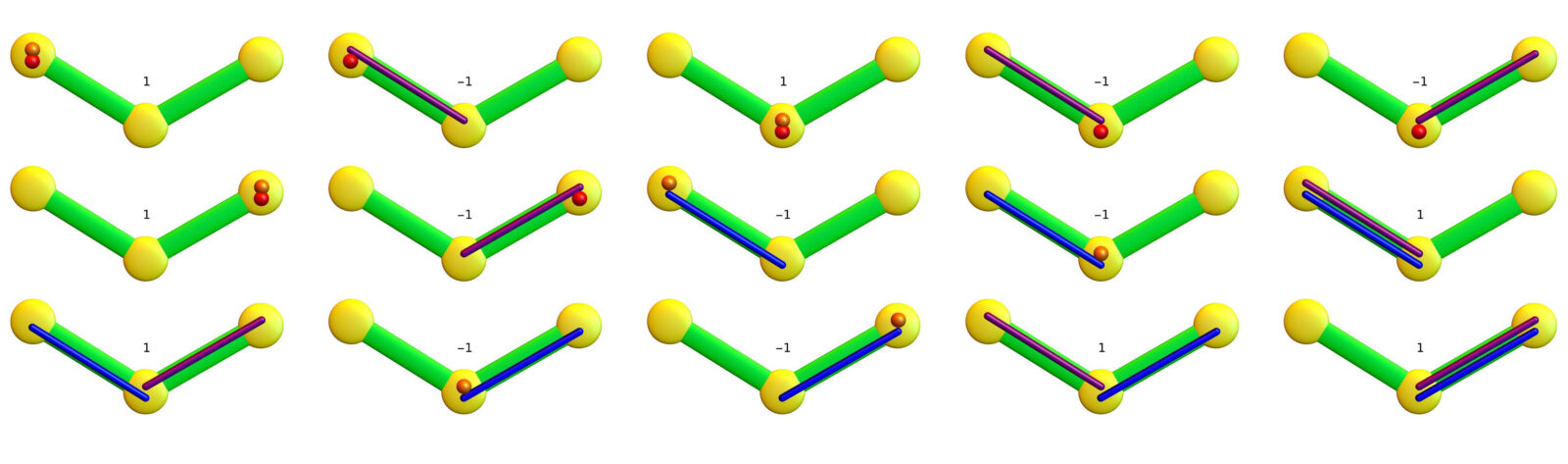As for the case m=1, where we have Euler characteristic $\chi=w_1$ , we have X(B(x))=1,X(U(x))=-1 and X(S(x))= X( {{1},{3}} ) = 2. Already the quadratic characteristic (Wu) is tougher. From the 25 pairs of simplices, 15 intersect. The total energy is $w_2(B(x))=-1$ . We illustrate this in the picture. The total energy of $U(x)=\{ \{1,2\},\{2\},\{2,3\} \}$ adds up 5 terms of energy 1 and 4 terms of energy -1 so that $w_2(U(x))=1$ . The unit sphere S(x) = {{1},{3}} is zero a zero dimensional sphere of Euler characteristic 2. Proposition 6 tells -1=1-2. Note that the general case to proposition 6 is very general as S(x) can be an arbitrary simplicial complex. Here is the picture with the 15 pairs of simplices that intersect in G:

Author: oliverknill