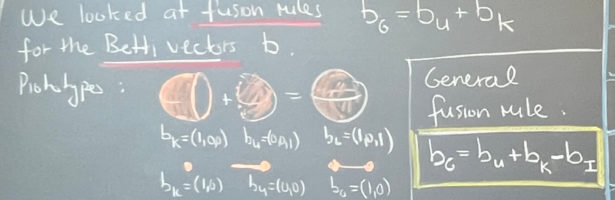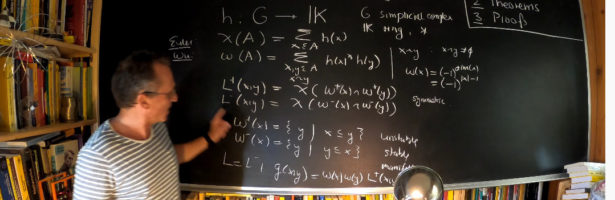A geometry is a space on which one has a derivative and notion of integration. This can be expressed more elegantly as a space with a cohomology as cohomology are kernels of matrices defined by the derivative and when looking at operators one needs a Hilbert space which intrinsically defines …
Causality Principle One of the most exciting principles in physics is the Huygens principle relating the geodesic motion with the wave dynamics. If we are in a Riemannian manifold, there are two type of “wave fronts”. We can look at the solution of the wave equation , where is the …
For slides and first remarks about the P-NP problem, see this page. I mentioned there my own personal predictions about the Millenium problems. See also this talk from 8 months ago about the perfect number problem in which also all Hilbert, Millenium and Landau problems are mentioned. So, here is …
Having talked a bit about GR (general relativity) and the SM (standard model), lets talk a bit about QM (quantum mechanics). Without any doubt, GR,SM and QM are three extremely successful pillars of modern fundamental physics. Their track record with experiments is monumental (*). We have played with simple games …
In 1960, Regge formulated a discrete calculus as a numerical scheme for relativity. We can formulate it as a theory on a weighted graph . where is a distance which is a discrete q-manifold. The graph defines a q-dimensional pure simplicial complex generated by the maximal complete subgraphs as facets. …
The topic is a combination of the “particles and primes” and geodesics in discrete manifolds” topics, I had worked on before. The first one is an elementary connection between primes in division algebras and particle phenomenology, the second is a completely deterministic dynamical system in combinatorics that has many properties …
AXIOMS: Most basic mathematical structures are heavenly in the sense that they would be discussed in any part of the universe. In algebra these would be groups or rings. In topology these would be topological spaces or metric spaces, in probability theory it would be sigma algebras and stochastic processes. …
We have seen last time that describing many particles moving on a manifold is best done by keeping on each cell a tag telling how many particles there are there. In other words, we do not evolve a sequence of maps but a divisor . This is more effective if …
On October 15, 2025, Sourav Chatterjiee gave the second of the Millenium prize lectures. I have started a page on this here where the slides are included. A bit of nostalgia Some of my own course assistants (when I was an undergrad) or grad student colleagues (when I was a …
If K(t) is a function in a Lie algebra then the Frenet equations Q'(t)=K(t) Q(t), Q(0)=1 defines a path in the corresponding Lie group. We can now use K(t) to define the Frenet path using the equation R'(t)=Q(t). This defines r(t), where r'(t) is the first row of R(t). The …
The arrow of time is probably one of the most written fundamental topics in physics. I myself have written about it once. To the right are some writings and movies related to time and these are only the movies or books I have seen. My favorite math book pair about …
A periodic Frenet curve in is up to isometry uniquely defined by a periodic curve in where the later describes the motion of the Frenet frame. Differentiation then defines a periodic curve in the Lie algebra . We can now reverse the story and start with a periodic curve in …
Maybe it is a good idea to add current “discovery code” also with the Dirac part. It can be helpful to post code also to be able to see in the future how one was thinking at the time. In the talk of Freedman, there was a slide with a …
Let (G,T) be a finite dynamical system. This means that G is a finite abstract simplicial complex and T is an invertible simplicial map (a permutation of G coming from a permutation of the vertex set V or alternatively, a homeomorphism of the topological space which origins from a permutation …
Yesterday was 9/16/25. You can easily check that it is the only date that is a Pythagorean triple MM/DD/YY. I tweeted And made a brief short on youtube about Elkies’s puzzle explaining visually that . If one is asked about the minimal number of puzzle pieces which can explain this …
Here is my “discovery code” used over the weekend to detect first experimentally that there are dynamical connection and green function matrices which are inverse of each other. I might talk about the proof next time. But first to the experiments. I take here a concrete example of a finite …
In the evening of the 13th of September after giving the talk below, it dawned me after doing lots more experiments that the connection dynamical connection Laplacian and the dynamical connection Green function that were written down on the right hand side of the black board work together if one …
When I had been studying mathematics at ETHZ, taking two semesters of calculus and at the same time taking two semesters of linear algebra had been mandatory. My Calc 1 (1a/1b here) and Calc 2 (21a here) teacher from the first year was Hans Laeuchli. His advisor Ernst Specker during …
When trying to translate everything that has been done in mathematics to the finite world it is good first to look at the most important theorems. Some of the theorems like the pigeon hole principle or the law of the product or the fundamental theorem of arithmetic do not need …
For a finite abstract simplicial complex, we can look at the Dirac Zeta function, the Connection Zeta function and the Lefschetz zeta function. My work on this in the last couple of years
Here is an other “poem” that has been added to the “math poetry page”. Given a simplical complex G, it computes the automorphism group Aut (its group of symmetries, meaning invertible simplicial mapss) and for each T computes both the Lefschetz number and the sum of the indices of the …
During a nice 23 K run on Friday, I was thinking a bit about Lefschetz. This is one of the first stories, I tackled. See the paper. It is one of my 10 favorite theorem in graph theory. I originally formulated it in graph theory in 2012 generalizing the one …
A conference earlier this year had the effect that some main stream media started to report about it. I saw it here in an Austrian journal. But the article does not report on any new discoveries. The 2025 Ultrafinitism Conference was also a cover story for NewScientist Magazine. I thought …
Given a finite abstract simplicial complex G, there are two amazing matrices which are two sides of a coin. Both matrices are symmetric n x n matrices if G has n elements. The Dirac matrix D =d+d* is defined by the exterior derivative d(x,y) = sign(x,y) if y is incident …
Let G=(V,E) be a graph with n vertices and m edges. So far all experiments indicate that also the signless Kirchhoff Laplacian |K| =D+A satisfies the Brouwer bound for all $late 1 \leq k \leq n$, where is the sum of the largest eigenvalues of |K| and . The signless …
If K is the Kirchhoff matrix of a finite simple graph with n vertices and m edges and eigenvalues and edge degrees . Define and and and . This is . Then the following general inequalities are known (the first 4 inequalities in the following list) or conjectured (the last …
One of the most amazing formulas in linear algebra is the Hadamard first variation formula which tells how an eigenvalue changes if the matrix entries are changed. Take a symmetric matrix K and perturb it as K+t E, where E is an other symmetric matrix. How do the eigenvalues change? …
John Walker (1949-2024) was an amazing programmer. His website “Fourmilab” was a page of inspiration for me since 1994, when the web started to get serious with Mosaic allowing to brouwse the internet. I still remember in early spring 1994, when I was busy finishing my PhD, that near our …
The elements of Euclid of Byrne (internet archive) are a nice example also in how to illustrate mathematics. The tools to illustrate mathematics have multiplied since Byrne’s time. Yesterday, I wanted to visualize the identity w(B(x))=w(U(x))-w(S(x)) for quadratic (Wu) characteristic which comes after linear (Euler) characteristic. In the video, the …
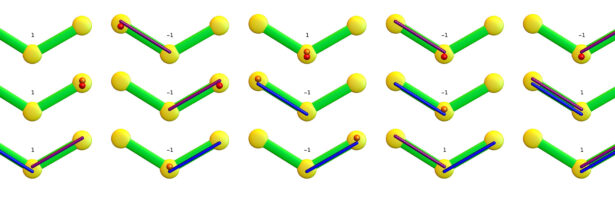
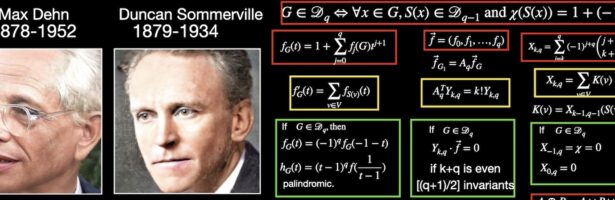
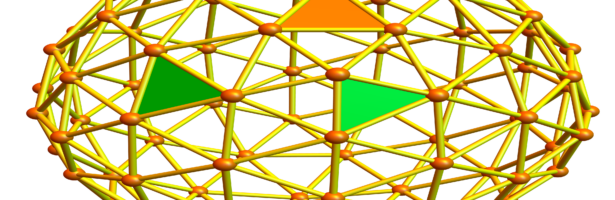
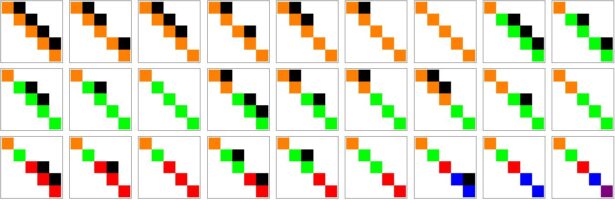
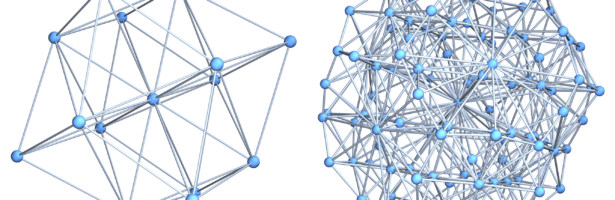
While thinking about some fundamental parts in the story of Dehn-Sommerville, I decided to make a bit of an exercise in imagining how Euclid would have done finite geometry. The result is given in the movie below. Euclid’s elements is undoubtedly one of the milestones in the whole of mathematics …
Next week, I will be back in my office. As they are constructing labs just near my temporay office, I made this “talk to myself session” in a seminar room of the department. I try to finish these days a review about Dehn-Sommerville, a rather unpopular topic historically speaking (not …
Dehn-Sommerville identities are symmetries for manifolds. First detected by Max Dehn in small dimensions, they were generalized by Duncan Sommerville in 1927. The relations were classically studied for simplicial polytopes which means q-spheres. It gives relations for the f-vector of a simplicial complex that is a q-sphere. The original work …
While walking through the ETH library in Zuerich on Monday, I saw a new book from 2025 by Brian Hopkins called “Hands-On Combinatorics: Building Colorful Trains to Manifest Pascal’s Triangle, Fibonacci Numbers, and Much More”. The ETH library is very nice. I used to work there myself often as a …
Summary We look at 5 results of Peter Lax (1926-2025) in a youtube short (1 minute clip) 1) 1956: Lax Pairs for integrable system2) 1990: Pedal Map in geometry: a chaotic system3) 1971: Approximation theorem of volume preserving continuous maps4) 1954: Lax Milgram theorem generalizing the Riesz representation theorm5) 1956: …
As promised in the talk, here are the 12 lines of code. The 13th line is an example and take the smallest 3 dimensional manifold G, the 16 cell which is a small example of a 3-sphere. The fiber bundle P has 384 elements in this case. Every single particle …
Here is the start of the novel “Schild’s ladder” by Greg Egan from 2004. It has sometimes been called the hardest SciFi Novel. Indeed, you can already be stuck in the first paragraph. The text describes the diamond lattice (there is a Wolfram demonstration file here by Sandor Kabai from …
One of the problems which has bothered me in the last couple of months is the fact that in a locally finite geometry G, it is improbable to get a notion of geodesics which satisfies the properties: 1. any two points can be joined by a geodesics, 2. there is …
After talking about this on Saturday, I tried some other things (this is a perfect topic to think about before getting to sleep or even contemplate about while sleeping). First of all, we can extend how to evolve the geodesic flow given a triangle t=(a,b,c) in a q-simplex x of …
[Update June 17, 2025: The Senior thesis: Spectra and Similarity by Jessie Pitisillides and the preprint on the ArXiv: (Segre Characteristic Equivalence) of Jessie Pitsillides.] Every linear algebra course battles the concept of similarity. We learn that trace, determinant, rank or eigenvalues allow to check whether two matrices are similar …
While teaching probability this semester, I had naturally to think again at the central limit theorem and took this as an opportunity to warm up a bit something I abandoned in 2022 after learning that what I was following has been understood already by mathematicians like Levy or Gnedenko. Still, …
A closed geodesic in a q-manifold is a q-manifold C with boundary dC. This boundary dC is a circle bundle. It can be for example. But it can also be a non-trivial bundle. Note that everything is purely combinatorial and pretty small. For the Moebius strip for example C is …
Given a q-manifold, we have a geodesic dynamics T:P -> P, where P is the oriented frame bundle. Most geodesics are not simple but we can look for the number of simple closed geodesics and so investigate questions close to the Ljusternik-Schnirelmann theme in the classical setup. For any 2 …
One can for discrete billiards ask questions which are classical in the continuum. One of them is Guillemin’s conjugacy problem, which is an inverse problem. It is problem 6 in my personal favorite list of open problems in Hamiltonian dynamics from 25 years ago. This is a problem which in …
[Update March 23: a paper draft is up. The ArXiv version contains also more code.] Spring break is a good time for some programming and cleanup. I reorganized our home office, took everything apart and rewired the half a dozen computers new, got rid of about 30 old harddrives, mostly …
This spring, scientific american was asking around in departments about problems mathematicians are thinking about. I immediately wrote back mentioning the “odd perfect number problem“, a problem which has for strange reasons been snubbed by problem collections. The article in SCIAM has now appeared. As I had once taken the …
Recently, monopoles was mentioned in a youtube episode of Hossenfelder’s show. For, me, it had always been more natural that monopoles do not exist. Let me explain. Electromagnetism is defined if one has a geometry with an exterior derivative d. This is very general and works for delta sets. The …
Riemannian geometry is related to general relativity, probability theory is related to quantum mechanics. Length enters in GR in the form of geodesics, paths of mass points and curvature, the deformation of space through mass. Probability enters in quantum mechanics by seeing solutions of wave or Schrödinger equations in terms …
Shortly after working on Gauss-Bonnet-Chern for graphs, I wrote about Poincare-Hopf for graphs. It took a larger part of the winter break 2011/2012 to come up with the formula where is part of the unit sphere where the function value is smaller than the function value at v. The function …
A discrete 2-manifold [PDF] is a finite simple graph for which all unit spheres have d(v)=4 or more vertices. The smallest example is which is the octahedron graph and where every unit sphere is a circular graph with 4 elements. The Eberhard curvature is very rigid: the Mickey Mouse theorem …
Curvature is a local notion in a finite geometry that adds up to a topological invariant. This is Gauss-Bonnet. I’m only really interested in curvatures that satisfy this exactly. This does not exclude sectional curvature, the latest venture because sectional curvature integrated over a geodesic sheet is the Euler characteristic …
We continue to look at examples of a-manifolds. Besides level sets we can also do connected sum constructions. In the talk, I glue together two manifolds along a q-simplex. An other possibility is to glue along a wall, a (q-1) simplex, removing two simplices attached at a hypersimplex and glue …
We have to adapt the geodesic flow in two situations: for manifolds with boundary or for manifolds obtained as level sets in other manifolds where we want to define the geodesic flow directly in the open set and not first pass to the Barycentric refinement. In both cases, we sort …
We continue the quest to define a sectional curvature for q-manifolds. A good notion should produce classical theorems like that if sufficiently pinched manifolds are spheres. Asking all embedded wheel graphs to have positive curvature was much too rigid and produced only spheres, so small that I called this the …
If G is a q-manifold, we have defined a geodesic dynamics T on the frame bundle P, a principle fiber bundle with structure group . As we have seen last time, the geodesic update step , where is the dual sphere of the -simplex . Everything is finite. G is …
The Shashibo puzzle is a game in the category of geometrically realized simplicial complexes of dimension q=3. One can also play it combinatorially, meaning to disregard geometric realization and just look at finite set of finite sets. One can see it as a playing with 3-dimensional complexes generated by twelve …
Here are two fundamental problems for discrete q-manifolds (a notion which can be defined for the trinity of geometric structures, that is for finite simple graphs as well as for simplicial complexes or delta sets). As for 1, one could ask that every embedded wheel graph has positive curvature. This …
Herbert Groetzsch and Jan Mycielski worked in the 50ies on the chromatology of triangle free graphs. Groetzsch’s 3 color theorem assures that planar triangle free graphs have chromatic number 3 or less. Mycielski defined an operation on graphs which preserves triangle free graphs and increases the chromatic number exactly by …
Coloring manifolds is a wonderful theme because it is not that well studied and so has many low hanging fruits. Here is an other one. For d-manifolds, the chromatic number is between d+1 and 2d+2 and a growth rate (3d+1)/2 is observed and reasonably conjectured upper bound. I started to …
The Regge approach to discrete relativity is also related to graph coloring problems of d-manifolds. While one can look at the length of the dual sphere of a codimension-2 simplex as a notion of curvature, the distinction of whether this circle has even or odd length is relevant when wanting …
The definition of soft Barycentric refinement needed adaptation so that it preserves manifolds with boundary. If G is a finite abstract simplicial complex. The Barycentric refinement is the Whitney complex of the graph in which G are the vertices and where two points are connected, if one is contained in …
A finite abstract simplicial complex G, a finite set of non-empty sets closed under the operation of taking non-empty subsets, has not only a wonderful topology in which the stars form a basis and the cores are closed, but also a hyperbolic structure as the unit sphere is the join …
General relativity plays on a pseudo Riemannian manifold (M,g). The Einstein equations describe how matter defines the space time and the geodesic equations describe how mass moves in space time. It is maybe the most beautiful theories that exist as it describes a relatively complicated frame work as part of …
What is the reason for the structure of the Standard Model? For a mathematician, it better has to be something inevitable. The model is the periodic system of elements is all based on the geometry of the space G one considers. If G has an exterior derivative, one has a …
The 2 dimensional plane can be characterized as the only simply-connected two dimensional flat manifold. In the discrete there is a similar uniqueness. The discrete hexagonal plane is the only 2-manifold that is flat and simply connected. Compact flat 2-manifolds like the torus or Klein bottle are not simply connected …
There is a soft Barycentric refinement of graphs or simplicial complexes which can be seen as the usual Barycentric refinement in which the second highest dimensional simplices are collapsed. It is a triangulation of the dual complex. The soft Barycentric refinement of a d-dimensional cross polytop for example is a …
A real symmetric matrix is called a Dirac matrix, if it is a block Jacobi matrix in which the side diagonal entries are nilpotent, meaning . For such a matrix, the square is called the Laplacian. It is block diagonal . If is a continuous function such that is invertible, …
A discrete geometry does not have a lot of symmetry as the automorphism group is in general empty. The isospectral set of the Laplacian or Dirac matrix is large enough however. Note that when dealing with a specific class of operators like Dirac matrices, then not all isospectral matrices qualify. …
Since finding the isospectral deformation of the exterior derivative (see “An integrable evolution equation in geometry” from June 1, 2013 and “Isospectral Deformations of the Dirac operator” from June 24, 2013), I tried to find discrete time integrable evolutions of the Dirac operator. Last Sunday, while experimenting in a coffee …
An abstract delta set (G,D,R) is a finite set G with n elements, a selfadjoint Dirac matrix with and a dimension vector defining a partition and Hilbert spaces called the spaces of k-forms. The exterior derivative maps to . The Hodge Laplacian is a block diagonal matrix defining the Hodge …
Explanations of the Casimir effect using common physics intuition like “polarization” (it originally was studied in the context of van der Waals forces) or “pressure” do not work. The reason in the case of the Casimir effect is that in the case of two planes or two cylinders the Casimir …
In this presentation, there is a bit of advertisement for finite geometry and delta sets in particular. I also tried to get a bit into the history of finitist ideas in geometry and physics(starting with Riemann). One usually thinks about finite projective spaces when talking about “finite geometries”. I like …
I looked at a quadratic cohomology example. For theoretical backgroun, see the ArXiv paper “Fusion inequality for quadratic cohomology”. It is the case when U is a union of two disjoint smallest open sets in a 2-sphere for which I take the Icosahedron, one of the Platonic solids and a …
While linear cohomology deals with functions on simplices, quadratic cohomology deals with functions on pairs of simplices that intersect. Linear cohomology is to Euler characteristic what quadratic cohomology is to Wu characteristic $w(G) = \sum_{x,y, x \cap y \in G} w(x) w(y)$. If the simplicial complex is split into a …
Delta sets are very general. They include simplicial complexes, open sets in simplicial complexes, quotients of simplicial complexes, quivers and so multi-graphs or simply hypergraphs, sets of sets. For the later, the geometry is not that interesting in general. As for quivers, the associated delta set is one dimensional only …
The smallest open sets in a finite topological space form the atom of space. It was almost 100 years ago, when one has turned away from non-Hausdorff topological spaces and decided they are less relevant (Hausdorff seems have convinced Alexandrov and Hopf to focus on Hausdorff property). This is unfortunate …
Historically, geometry started in Euclidean spaces. There was no concept of coordinate when Euclid wrote the “elements”. Using “points” and “lines” as building blocks and some axioms, the reader there is lead to quantitative concepts like “length”, “angle” or “area” and many propositions and theorem. Only with Descartes, the concept …
Finite geometric categories: graphs – simplicial complexes -simplicial sets – delta sets Delta sets were originally called semi-simplicial sets by Samuel Eilenberg and Joseph Zilber in 1950. Similarly than semi-rings are more general than rings or semi-groups are more general than groups, also delta sets are more general than simplicial …
The discrete Sard theorem in the simplest case (which I obtained in 2015) that a function from a discrete d-manifold to {-1,1} has level sets that are (d-1) manifolds or empty. (See here for the latest higher generalization to higher codimension.) A simplicial complex is a d-manifold if every unit …
Here are some links to the articles mentioned in the talk: It surprisingly often happens that a big conjecture tumbles at around the same time. In the case of the Arnold conjecture, several approaches, spear headed by Conley-Zehnder, Eliashberg and Floer have reached the goal. But also almost always with …
The last geometric theorem of Poincare was conceived shortly before the death of Poincare. Poincare had a prostate problem when he was 58 and went to surgery in 1912 which he did not survive. Fortunately his last theorem was sent to an Italian journal two weeks before he died, but …
Finite topological spaces are only interesting if non-Hausdorff. The reason is that every Hausdorff finite topological space is just the boring discrete topology. The topology from a simplicial complex is an example of a nice and interesting topology because it produces the right connectivity and dimension on the complex without …
It is not quite yet a poem, but here, as promised in the movie, some code to generate both the Betti vector and Wu betti vector of a random submanifold in a given manifold. It is 25 lines without any additional libraries, so not yet quite a poem, but it …
My experiments so far indicate that the Wu cohomology of a d-manifold G can be read off from the usual cohomology. If is the Betti vector of G then (0,\dots,0,b_d,b_{d-1},\dots,b_1,b_0)$ appears to be the Wu Betti vector. So far, this is only a conjecture. In the talk, the case , …
[Update 3/5/2024: given that one knows now the optimal Moebius strip, one can wonder about the much easier question of what the smallest simplicial complex producing a cylinder or Moebius strip is. Below, I use in both cases 6 facets (triangles). For the Moebius strip, one can do with 5 …
The video below is an attempt to get back to an older story of Wu characteristic. One of the things which still needs to be explored badly is the Wu cohomology of the complement K of knots H and more generally of the complement K of k-dimensional manifolds H in …
Here is some code illustrating the story. We take the 4 manifold (a favorite manifold of Heinz Hopf) and consider two random functions f,g. Now generate the two manifolds and . They are both 2 manifolds. It goes as follows: the sign data of {f,g} are in which are 4 …
In my paper “Manifolds from Partitions”, I stated that that the case of empty graphs can not occur, but did not prove it. It is indeed not true. Here is an update [PDF] with an additional section. It is very rare although that a surjective map produces still an empty …
My experience from my Schweizer Jugend Forscht adventure was not only invaluable from the scientific point of view, I also met some other young aspiring scientists (here is the book with all the participants (PDF)) which was published in 1983 (when I was already a second year ETH student), and …
A nice thing about mathematics is that it has no dogmas, statements which have to be taken on good faith. Axioms come closest, but by nature also, they come with an honest warning that one can either accept them or not. Already Euclid fought with the parallel axiom. Today it …
Brevity contributes both to clarity and simplicity. Surprisingly, it often contributes to generality. I myself am obsessed with brevity. I especially love short code. A short program is like a poem. If it is also effective, it can also be used as building blocks of larger programs. The Unix philosophy …
Happy new year 2024. Here is the code displayed on the right upper corner of the board written this morning when wondering how frequent the situation is that the year is divisible by the year modulo 1000 minus 1. This happens for 2024 as it is divisible by 23. The …
First about Sard: (a write-up [PDF] ). I also display a bit my hobbies: Panorama photography (since 1999, a time when panoramas were still stichted). Later with a mirror camera. Then with GoPro Max, Iphone and more recently with the insta 360 camera (I for strange tech enhousiastic reasons pride …
In the program to get rid of any notion of infinity, one necessarily has to demonstrate that very classical and entrenched notions like topics appearing in a contemporary multi-variable calculus course can be replaced and used. Artificial discretisations do not help much in that; they serve as numerical schemes but …
There are lots of finite geometric structures. Graphs are probably the most clear ones. Simplicial complexes can not be beaten in simplicity. And delta sets can not be surpassed by generality. So, they are a geometric incarnation of the paradigm “Simplicity, Clarity and Generality”, which appeared on the book cover …
Here is the table shown in part 2 of the presentation showing some of the toys. It had been generated by Mathematica. It uses manifolds from the manifold page of Frank H. Lutz mentioned in the clip. About the left hand side (of the chalkboard) with some history pointers of …
One of the nice things in mathematics is that one can play with models which do not necessarily have to do directly with the real world, whatever the later means. We can look at abstract objects, like finite simple groups, number theory in some number field or topology in 1001 …
What is {f=0,g=0} for two functions f,g on a graph G. If G is a 4-manifold, these are 2-manifolds or empty.
Arboricity and Chromatic number are linked in various ways. The topic also links to difficult NP complete problems. We muse about how often it is the case that for manifolds the question is easy. An example is the Hamiltonian path problem which is linked to Peg Solitaire
One of the nice things to work in a subject not having grown up in is to be in steep learning curves. I have thought about the arboricity of manifolds for a while now but the fact that the arboricity can be arbitrary large for d-manifolds with d larger than …
We explain why the arboricity of 3 spheres can take values between 4 and 7 and mention that for 3 manifolds the upper bound is 9 (but believed to be 7).
We look at the problem to find the possible arboricities which a 3-sphere can have.
The three tree theorem tells that any discrete 2-sphere has arboricity exctly 3.
A notion of a discrete vector should work for theorems like Poincare-Hopf and also produce a dynamics as classically, a vector field F, a smooth section of the tangent bundle on a manifold produces a dynamics . A directed graph does not give a dynamics without telling how to go …
We discuss briefly how to make the cohomology space of a graph into a cohomology ring. In other words, how to define the cup product on the kernel of the Hodge Laplacian.
About the cohomology of measurable sets in a probability space equipped with an automorphism.
Something about knots and something about topological data analysis and something about the general frame work to do mathematics in a finite setting.
A bit the bigger picture about the mathematical and data structures which come in when working on these finite geometries.
A youtube presentation of May 13, 2023. We point out that we have a relatively simple approach to Eilenberg-Steenrod.
Over the winter break I started to look at Mayer-Vietoris type rules when looking at cohomology of subsets of a simplicial complex. See January 28, 2023 (Youtube) , and February 4th 2023 (Youtube) and most recently on February 19, 2023 (Youtube). Classically, cohomology is considered for simplicial complexes and especially …
A finite abstraact simplicial complex or a finite simple graph comes with a natural finite topological space. Some quantities like the Euler characteristic or the higher Wu characteristics are all topological invariants. One can also reformulate the Lefschetz fixed point theorem for continuous maps on finite topological spaces.
We report on some progress on analytic torsion A(G) for graphs. A(G) is a positive rational number attached to a network. We can compute it for contractible graphs or spheres.
The results mentioned in the slides before are now written down. This document contains a proof of the energy relation . There are several reason for setting things up more generally and there is also some mentioning in the article: allowing general rings and not just division algebras extends the …
The energy theorem for simplicial complexes equipped with a complex energy comes with some surpises.
If a set of set is equipped with an energy function, one can define integer matrices for which the determinant, the eigenvalue signs are known. For constant energy the matrix is conjugated to its inverse and defines two isospectral multi-graphs.
The counting matrix of a simplicial complex has determinant 1 and is isospectral to its inverse. The sum of the matrix entries of the inverse is the number of elements in the complex.
