Lefschetz

During a nice 23 K run on Friday, I was thinking a bit about Lefschetz. This is one of the first stories, I tackled. See the paper. It is one of my 10 favorite theorem in graph theory. I originally formulated it in graph theory in 2012 generalizing the one dimensional case of Nowakowski and Rival from 1979. It was common at that time that graph theorists would look at graphs as one dimensional simplicial complexes and not capable of modeling almost arbitrary simplicial complexes. In the winter of 2022, I seriously started to think about finite topologies and Lefschetz appears here in this video. In the spring of 2024, I ought about the fixed point theorem also in the context of delta sets.

The question I pondered during my run is whether one can really do the Lefschetz theorem for continuous maps rather than simplicial maps. Simplicial maps come from a map on the vertices. A continuous map does need to have that property. A constant map from G to one of its non-vertex simplices for example is continuous but not a simplicial map. When we talk about topology on a delta set it is always the Alexandrov topology generate by the stars which is the topology in which the simplicial sub-complexes are the closed sets. Note that G is by definition already a set of sets so that the topology on G is a set of set of sets. An example of an open set in . One of the difficulties of dealing with continuous maps is that one has to add some calculus again. If one just gives a map from G to G that is continuous in the finite topology we do not yet know what happens with the orientations of the individual simplices. One has to implicitly assume for example that the orientation does not change. Otherwise, we get confusion. Lets for example take which is the identity map but twisting the orientation of the edges in G. Now, all simplices are fixed and the index of each simplex is 1. What goes wrong is that the Koopeman operator Uf=f(T) does not commute with the exterior derivative: d Uf (a,b) = f(a)-f(b), while U df = U(f(b)-f(a))=f(b)-f(a). For a simplicial map, where the transformation T comes from a map , where V is the set of zero dimensional simplices, things work naturally. Maybe we just have to axiomatically assume that UD=DU so that U leads to a chain homotopy between the chain complex on G and the chain complex on T(G).

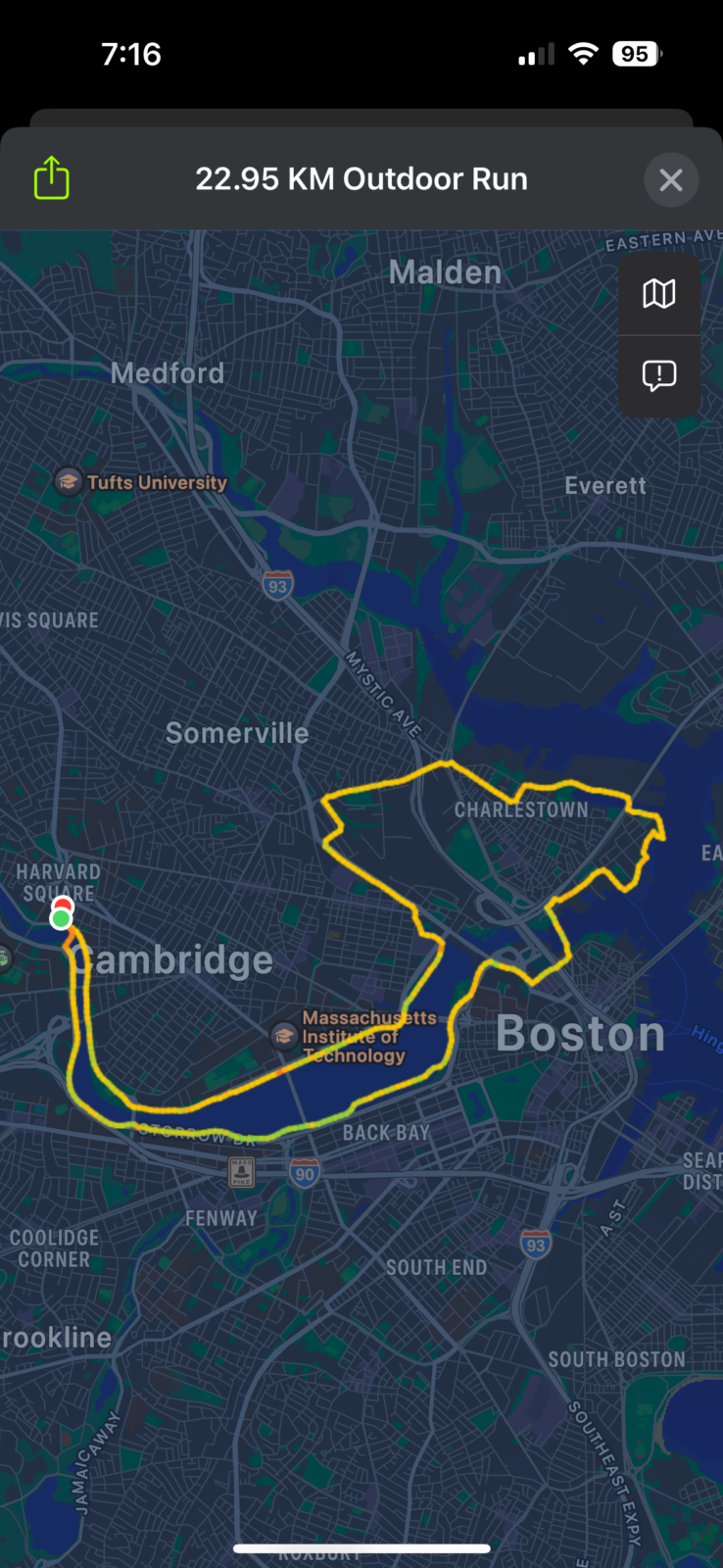
[Side remark: The run from yesterday was very nice, warm but not too hot weather. I tried a bit to maximize the time spent near water. The route along the Charles to the Science museum and back was actually the first run I have ever done here in Boston, when I interviewed for the Harvard job in December 1999. My talk from December 17, 1999 is here [PDF]. I had as part of the interview given a math table talk in lecture hall SC 507 and there had been quite many students present. The department had been very nice. I could lodge in the faculty club and join a breakfast in the Leverett dining hall. I had also been taken to the question center, which had been still in the basement of Memorial hall and I had to (part of my interview) answer questions live on partial differential equations in Math 21b. In 1999, the course still had quite serious Dirichlet problems to be solved, requiring more than just Fourier theory. Anyway, the running on the Charles always remembers a bit the first run. I like also very much to run through Charlestown, pass under the Momorial bridge and then follow the Charlestown Naval Shipyard park, the Constitution, pass North station and then get back to the Charles to follow it until the Weeks footbridge. The drone pictures on the following video show a bit the area.]