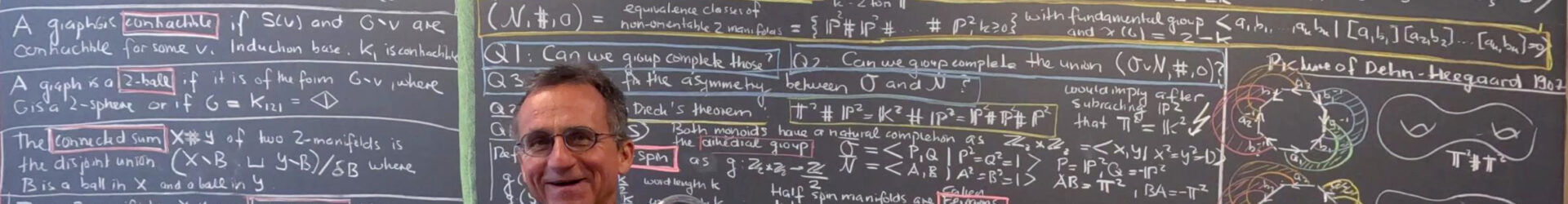Group Completing Manifolds - Quantum Calculus

Manifolds are in the following two dimensional, compact, connected and without boundary. Their classification of these geometric objects is a classical piece of mathematics, completed in a satisfactory way in 1907 by Dehn and Heegaard: the structure is that there are two monoids. The monoid $(\mathcal{O},\#,0)$ of orientable manifolds that is generated by the 2-torus $\mathbb{T}^2$ . The k-th sum has Euler characteristic 2-2k. Then there is the monoid $(\mathcal{N},\#,0)$ of non-orientable manifolds generated by the projective plane $\mathbb{P}^2$ . The k’th sum has Euler characteristic 2-k. The 0-element 0 in both monoids is the 2-sphere. The summation is the connected sum. To solve the asymetry between orientable and non-orientable situations and to get groups, we introduce a ribbon A and anti-ribbon B such that T=A#B. We also introduce an anti-projective plane Q. Now the group of orientable manifold is $\overline{\mathcal{O}} = \langle A,B| A^2=B^2=0 \rangle$ . Similarly the group of orientable manifolds is $\overline{\mathcal{N}} = \langle P,Q | P^2=Q^2=0 \rangle$ . Define the genus or spin of a word PQP… as half the number of letters in it and for a word QPQ… as minus half the number of letters in it. This is now the Euler characteristic for all manifolds. Manifolds with half integer spin are called Fermions. Manifolds with integer spin are Bosons.

Author: oliverknill