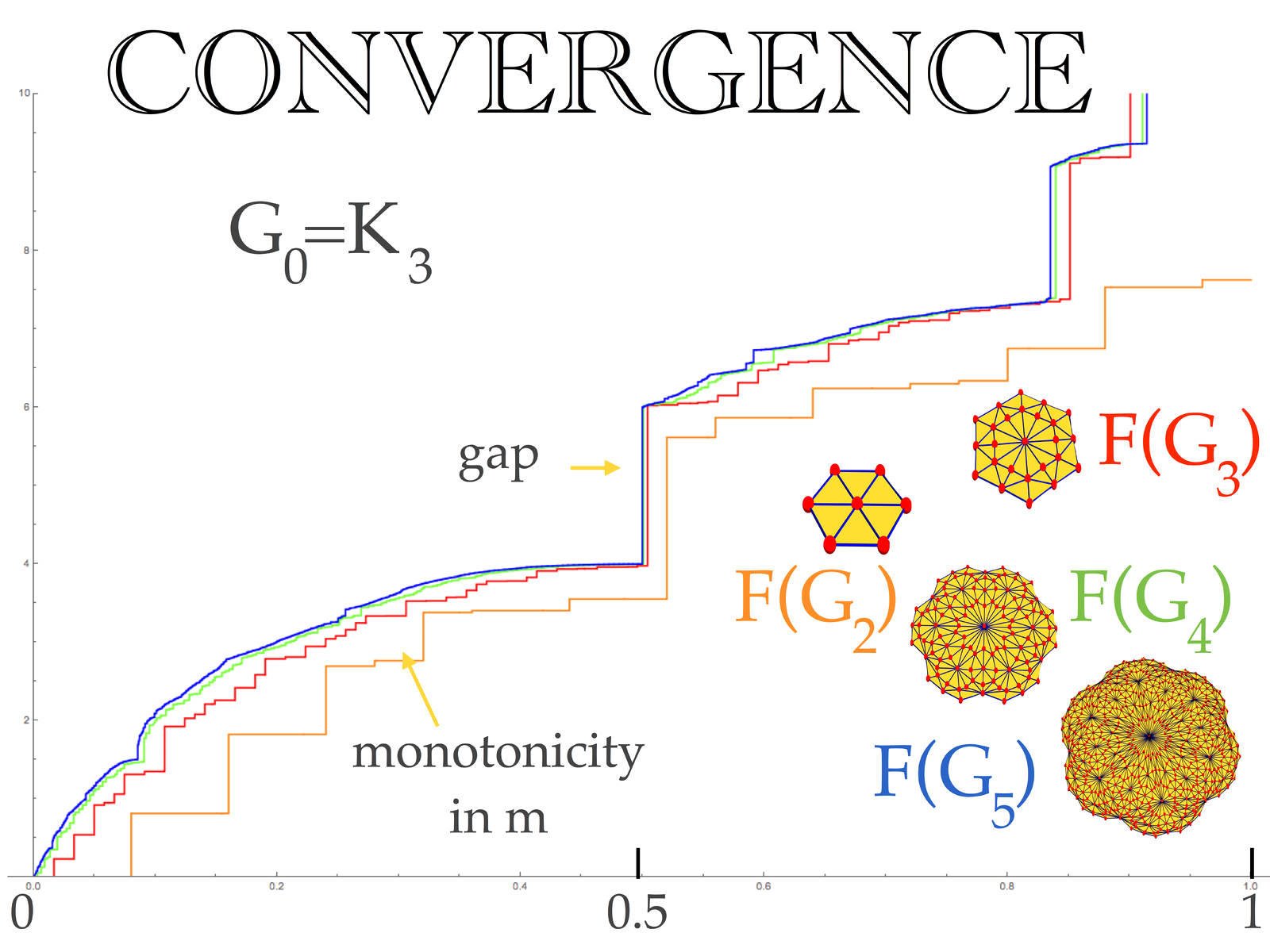
When passing from the discrete to the continuum, topologists have invented Barycentric subdivision. This is usually done in a Euclidean setting. When thinking about topology in a quantum way, we don’t want to use Euclidean space but start with discrete structures. Combinatorial topology has come up with the concept of Barycentric subdivision for abstract simplicial complexes. These are structures imposed on a set which similar than topological, order, measure or algebraic structures are given by a specifying a set of subsets, in this case a set of non-empty subsets which are closed under the operation of taking non-empty subsets. Barycentric subdivision takes this set of subsets as basic point set and builds a new simplicial complex structure on this, given by the order structure. If you think this set-up is hard to understand, I agree as simplicial complexes usually are introduced later in a mathematics curriculum. Much more intuitive and approachable is the language of graphs. A finite simple graph G=(V,E) comes naturally equipped with a simplicial complex: It is the Whitney complex which consists of the set of all subsets which form complete graphs. The Barycentric subdivision of a graph is a new graph, where the complete subgraphs are the new vertices and where two such new points are connected, if one was originally contained in the other. This immediately produces a holographic picture as once the subdivision is done, one can repeat it. The basic idea is to look at complete sub graphs of a graph as points. If one takes this seriously then already a Barycentric limit is intrinsic in the finite structure. If the original graph has no triangles or -if one looks at graphs equipped with the 1-skeleton simplicial complex structure as many graph theorists do – then the Barycentric limiting space is the topological group of dyadic integers. This is a quantum analogue of the circle but unlike the circle, which has a continuum of translations, there is a smallest translation in the group of dyadic integers. It is called the adding machine. In ergodic theory (that’s how I got into it), the dynamical system is known as the von Neumann Kakutani system, an interval exchange transformation which is the unique dynamical system which is a fixed point of the 2:1 integral extension. Unlike the usual integers, the dyadic integers form a compact space and space is quantized in the sense that there is a smallest translation. What is interesting is when one looks at the Laplacian of the limiting structure. The Laplacian is a fundamental object in any geometry as it allows to define what “light evolution” is and since light can be used to measure distances, it allows to recover all the geometry. It turns out that the Laplacian of the Barycentric limiting geometry is universal. (See The graph spectrum of barycentric refinements and Universality for Barycentric subdivision.) In the one dimensional case, its spectral density of states is the equilibrium measure of a Julia set of the quadratic map belonging to the “tail” -2 of the Mandelbrot set. Unlike most Julia sets, it is a smooth measure and still self similar. The inverse of the integrated density of states satisfies F(2x) = T F(x) where T is a quadratic map. If one looks at the situation in 2 or more dimensions, the limiting density of states is universal too but it is not identified yet. The spectral behaviour is no more smooth as in the one dimensional case. There appear gaps in the spectrum: 
There is an other story appearing when looking at Barycentric subdivision. If one counts how the number of points grows under subdivision, one can encode this with a single universal matrix A whose eigenvalues are k!. The eigen vectors of its transpose are produce Barycentric characteristic numbers, where the first one with eigenvalue 1 is Euler characteristic. The picture immediately shows that Euler characteristic is unique in the sense that it is the only valuation which is a homotopy invariant assigning the value 1 to points. The other invariants scale under Barycentric refinement. But there is a surprise: for geometric graphs, half of them vanish! This is related to Dehn-Sommerville-Klee invariants which have been known for a while. One can prove this elegantly using ideas from differential geometry: there is a Gauss-Bonnet, Poincare-Hopf result as in differential geometry or differential topology (its just much easier to understand). It turns out that Gauss-Bonnet is the expectation over Poincare-Hopf if one averages over all possible functions (waves). This is very nice. And now the quantum calculus ideas discussed before in the context of the Sard theorem kicks in. One can write the Poincare-Hopf indices (integers!) as invariants of smaller dimensional spaces allowing induction. This is outlined here kept as a 2 page document so that can be tweeted.
Some video: