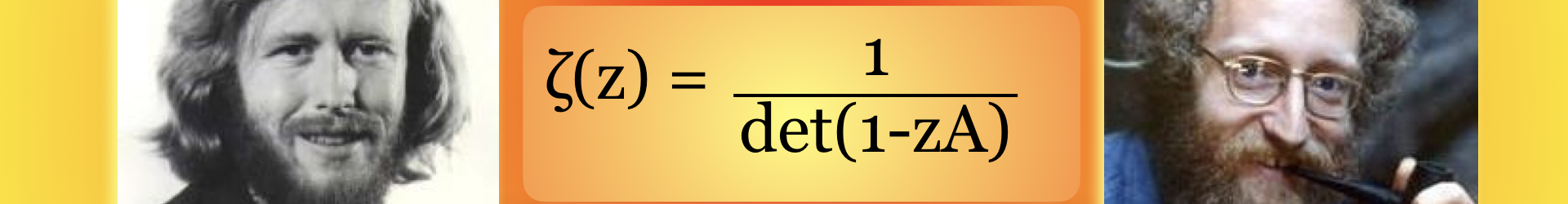On Bowen-Lanford Zeta Functions
Graph theory

On Bowen-Lanford Zeta Functions

Zeta functions are ubiquitous in mathematics. One of the many zeta functions, the Bowen-Lanford Zeta function was introduced by my Phd dad Oscar Lanford and Rufus Bowen. I am in the process to wrap up a proof of a theorem which is so short that its statement can be done in 140 characters: A finite simple graph G=(V,E) defines H=(W,F) where W={simplices in G}, F={(a,b)| a intersect b}. If A=adjacency of H then 1+A is unimodular. See the actual twitter announcement and the math table handout [PDF]. The proof is still quite complicated. The result was found in February 2016 when doing experiments related to intersection calculus. As we will see, one can reformulate the theorem in terms of the Bowen-Lanford zeta function of an intersection graph at z=-1 is either -1 or one. Actually, we know even that it is 1 if and only if the number of odd dimensional simplices in the original graph is even. Before we go into into the mathematics, a short explanation why this belongs to quantum calculus: we think of a graph as a geometric object on which one can do calculus. While the Fredholm determinant of the intersection graph of a graph G is not invariant under Barycentric refinements, it appears that the values of the inverse matrix (1+A(G’)) are invariant under Barycentric refinements of the graph G. If this is true then can again use this discrete intersection calculus to attach invariants to continuum geometries and distinguish spaces topologically.

Bowen Lanford Zeta functions

Given a geometric space there are two major ways to attach a zeta function to it. Given a Laplacian L=D2 one can look at the positive eigenvalues of D and form the sum \zeta(s)=\sum_n \lambda_n^{-s}. An example is D=i d/dx on the circle, where the positive eigenvalues are n with eigenvectors \exp(-inx). This works for any compact Riemannian manifold or for any finite simple graph. An other possibility is to look at a dynamical system, a time evolution on the space like a map T on the space for which {\rm Fix}(T^n) is finite for every n>0. The Artin-Mazur \zeta function is then defined as \zeta(z)=\exp(\sum_n |{\rm Fix}(T^n)| z^n/n). In the case of a finite simple graph, there is a natural time evolution, the subshift of finite type defined by the graph. In that case, the Artin-Mazur zeta function simplifies to 1/det(1-zA), where A is the adjacency matrix. It is called the Bowen-Lanford \zeta function. One can rewrite the function as a product \prod_p (1-p^{-s})^{-1}, where the product is over all prime orbits of T and p=\exp(|P|) where P is the orbit, |P| is the length and s=\log(z). It was just written in such a way that it looks like the Riemann zeta function again which is by Euler \prod_p (1-p^{-s})^{-1}, but where p runs over all the primes.

bowenlanford1 Oscar Lanford Rufus Bowen

Fredholm Determinant

Given a trace class operator A, one can define \det(1+A). It is 1/\zeta(-1) with the above notion of \zeta function and called Fredholm determinant. In the case when A is the adjacency matrix of a graph, then one can interpret \det(1+A) as a sum over all oriented paths (not necessarily connected) over the vertex set. The identity matrix 1 in 1+A has added the possibility that a path also stays at the same spot. A similar change happens when looking at the Laplacian L rather than the adjacency matrix, where the pseudo determinant det(L) gives the number of rooted spanning trees in the graph and det(1+L) the number of rooted spanning forests.

Leave a Reply