Let G=(V,E) be a graph with n vertices and m edges. So far all experiments indicate that also the signless Kirchhoff Laplacian |K| =D+A satisfies the Brouwer bound for all $late 1 \leq k \leq n$, where
is the sum of the largest
eigenvalues of |K| and
. The signless Laplacian is interesting because of the Hydrogen identity . This identity relates |H| with the connection Laplacian L
, where
is the Hodge Laplacian. I called the operator
the hydrogen operator because of its formal lose formal similarity with the Hydrogen operator in chemistry
where
and
are constants. Now the inverse of the Laplacian in 3-dimensional space has a 1/r kernel. It is an integral operator different from the multiplication operator with U(r)=1/r but it has a similar structure like
in the sense that the Green function of the Laplacian (the kernel of the inverse) guides the electro static (and of course also gravitational) 1/r potential. The Brouwer inequality
relates the sum
is the sum of the largest k eigenvalues of the signless Kirchhoff Laplacian with the number of edges and k. It is an open question whether it holds, like Brouwer’s conjecture but it would imply it.
Experimental observation (This Summer 2025): The Brouwer inequality holds also for the signless Kirchhoff Laplacian |K|. This is a variant than the Brouwer inequality. The spectral radius of |K| is larger or equal than the spectral radius of K.
Why am I excited about this? Because there is an easier interlacing going on for the connection Laplacian. I only discovered this this summer in the context of the Brouwer conjecture but I do not know yet how to use it. Maybe the following observation is a start. Could it be that the strong conjecture for the signless Laplacian is easier to prove because we have more structure? The Hydrogen identity had already been useful to give upper bounds on the spectral radius because knowing about the spectral radius of L immediately gives bounds on the spectral radius of |H| and so about H and so about the Kirchhoff matrix. But lets first look at the observation (once you see it, it is obvious):
Interlacing observation (This Summer 2025) : if L is the (n+m) connection Laplacian of a finite simple graph G with n vertices and m edges. Let H be a subgraph in which one of the edges of G has been deleted. Then the connection Laplacian of H is a principal submatrix of the connection Laplacian of G. This means that the spectrum of the reduced graph is interlaced with the spectrum of the original Laplacian.
This is exciting because in the proof of the general identity for graphs, we needed to escape to quivers in order to prove the result. Now we can prove upper the upper bound for the k’th eigenvalue of L as
as before which implies the upper bound for the signless Kirchhoff Laplacian and so for the Kirchhoff Laplacian. It is really nice to work with the connection Laplacian L which is a 0-1 matrix unlike the Kirchhoff matrix, which has a more complicated structure. And especially because L has an explicit inverse, the Green operator
which has the property that
can be interpreted as the potential energy between the simplex i and j. The potential of a point x is the Euler characteristic of star of x which is 1-deg(x). The potential between an edge and a vertex is 1 if they intersect. The potential between two vertices that are connected is -1. This Green function matrix (there was also a long battle to get the formula
which I called the Green Star identity as the stars of the simplices determine the Green function entries. Also the Green star identity is true in arbitrary dimensions and was later generalized from 2-point interactions to arbitrary k-point interactions where Green functions are a k-tensor giving the potential energy between any k-point simplex configuration and no more a matrix.
There is a bit of linear algebra to unpack here: first of all, the connection Laplacian L is like the Hodge Laplacian H a matrix. Let
denote also the 1-dimensional skeleton complex of the finite abstract simplicial complex defined by the graph. It is the set of vertices and edges. The definition of L as as follows: The entry
is equal to 1 if the simplices i,j intersect and 0 else. By the unimodularity theorem I proved in 2016 (after many months of failures) tells that the determinant of L is either 1 or -1, in general for any finite abstract simplicial complex. In the one dimensional case, I later proved the Hydrogen identity
, where H is the signless Hodge Laplacian. Unlike the unimodularity theorem, which holds in arbitrary dimensions, the Hydrogen identity only holds for one dimensional simplicial complexes, where the Hodge Laplacian has two blocks. I proved also that in general, the Euler characteristic of the complex (in arbitrary dimensions) is equal to the number of positive eigenvalues of L minus the number of negative eigenvalues of L. “One can hear the Euler characteristic” of a simplicial complex if one listens to the connection Laplacian!
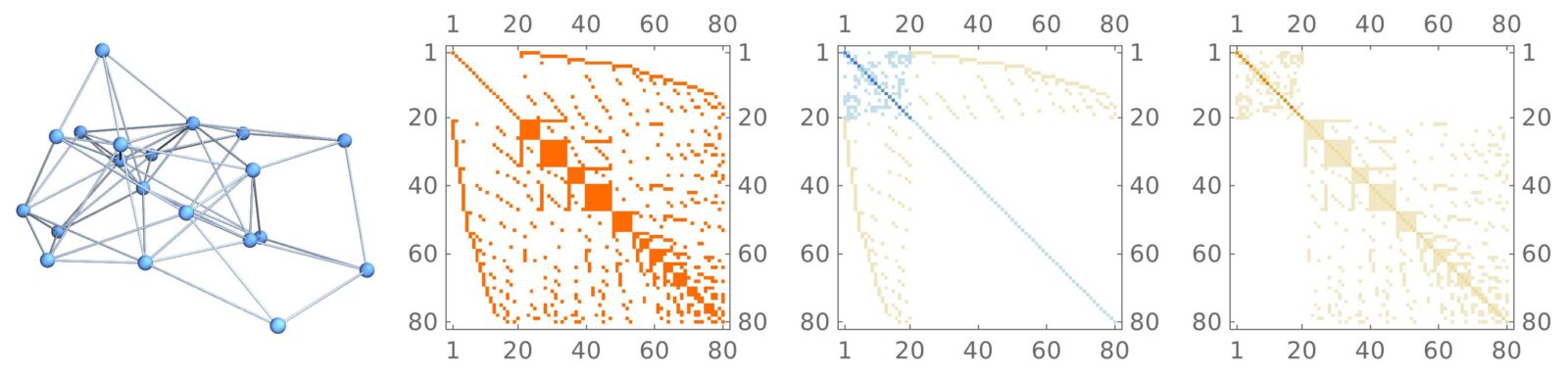
Lets look at some pictures. In the next row, we first see a random graph with n=20 vertices and m=60 edges. Then we see the connection Laplacian which is a 80 x 80 matrix. It is a 0-1 matrix. Then we see the Green function matrix then the matrix
which has two blocks. The first block is the signless Kirchhoff Laplacian. The second block is the signless 1-form Laplacian.