Connection and Dirac Matrix

Given a finite abstract simplicial complex G, there are two amazing matrices which are two sides of a coin. Both matrices are symmetric n x n matrices if G has n elements. The Dirac matrix D =d+d* is defined by the exterior derivative d(x,y) = sign(x,y) if y is incident to x of codimension 1 and d(x,y)=0 else. The connection matrix L is defined as L(x,y)=1 if x and y intersect and L(x,y)=0 else. Both matrices have some interesting properties.

References: having learned about McKean-Singer as a student (from the Cycon-Froese-Kirsch-Simon book), looking at the Dirac matrix D=d+d* was natural. See this talk from 2013. It is not only a notation simplification to look at one exterior derivative d on all forms rather than a sequence of exterior derivatives as Betti and Poincare did. There are thousands of discrete approaches to traditional geometry but most of the time, the notation is a tragedy. The adaptation of Hodge theory (from the 1930ies) to the discrete came swift by Eckmann in the 1940ies (I saw a talk of Eckmann in the 1980ies about the theme of Euler characteristic). The unimodularity theorem for the connection Laplacian was proven first here. Some spectral properties like the “hearing the Euler characteristic and the Hydrogen identity and the Green star formula appeared here.

Topology: the Hodge matrix is block diagonal. The kernel of block $H_k$ is the k’th cohomology group of G. Its dimension is the k’th Betti number . These are homotopy invariants. The connection matrix has both positive and negative eigenvalues. The number of positive eigenvalues minus the number of negative eigenvalues is the Euler characteristic . The determinant of is the Fermi characteristic .

Super symmetry: one of the most amazing things which hold in general is that the non-zero spectrum of H restricted to even forms agrees with the non-zero spectrum of H restricted to odd forms. I had learned that in the continuum from the book of Cycon-Froese-Kirsch and Simon when I was a grad student and noted in https://arxiv.org/abs/1301.1408 that this also holds in the discrete. I had been very excited about this because it appeared to have been unnoticed before in combinatorial set-ups. And it turned out to be an absolute gem also later on. Both the Euler-Poincare formula for Euler characteristic and its generalization, the Brouwer-Lefschetz fixed point formula can be proven elegantly using this super symmetry. The argument (I wrote about this so many times, it must be tiring) is that since the super trace of is zero, the super trace of is Euler characteristic indepdent of t. For t=0 it is the super trace of the identity matrix which is the combinatorial Euler characteristic. In the limit t going to infinity, it is the super trace of the projection onto the Harmonic forms (cohomology) which is the cohomological Euler characteristic. A similar argument works for the Brouwer Lefschetz formula which tells that if T is a continuous map from a simplicial complex onto itself (continuous in the finite topology of course, we never go to the continuum!) then the super trace of the Koopman operator on cohomology (which is the Lefschetz number) agrees with the sum of the indices of fixed points (simplices) of T. I had proven this first in https://arxiv.org/abs/1206.0782 using a method close to Hopf but it follows also by deformation. For t=0, the super trace of the Koopman operator is the sum of the indices of fixed points of T, while for t to infinity, this is the super trace on cohomology aka Lefschetz number. The deformation proof is cool because it immediately also generalizes to more elaborate cohomologies like Wu cohomology or higher cohomologies, where we also have Poincare Hopf and Lefschetz. Obviously it generalizes to any “differential complex” and so is Atiyah-Singer (generalizing Euler Poincare or GaussBonnet) or Atiyah-Bott like (generalizing the Lefschetz fixed point formula). I wrote about this once. The reason is that all we really need is a Dirac matrix D. This can come also from deformed Dirac matrices. All this goes also way beyond simplicial complexes and works for abstract delta sets as they have an exterior derivative and so a Dirac matrix.

Eigenvalue estimates: both the Dirac matrix as well as the connection matrix allow for eigenvalue estimates , where in the Dirac case we have the degree of the Dirac graph with G as vertices if two vertices are connected if d(x,y) is not zero. In the connection matrix case it is the degree of the connection graph where again G is the vertex set and two are connected if they intersect.

Isospectral deformation: both the Dirac matrix as well as the connection matrix can be deformed using a Lax deformation. In the case of the Dirac matrix, this produces a deformation of the exterior derivative which when d is used to measure distances using the Connes formula, leads to a naturally expanding space. The deformation works of course also in the connection case, but it is not clear whether there is an interpretation.

For open sets: the complement of a sub-simplicial complex in G is an open set U in the Alexandrov topology. The Dirac matrix and so cohomology is well defined. We have the fusion inequality for the Betti numbers if is a complementary pair of closed and open sets. In the connection case, the connection matrix of an open set is most of the time no more unimodular. Already for $U=\{ \{1\},\{1,2\} \}$ the connection matrix is a matrix with constant values 1 everywhere and is not invertible.

Hydrogen inequality: for one-dimensional complexes, there is a relation between the more Bosonic story for L and the more Fermionic story for D. We have , an identity we called the hydrogen identity. In higher dimensions hydrogen operator $L-L^{-1}$ does no more have the block structure.

Higher characteristic: the Hodge story for higher characteristics parallels the Hodge story for Euler characteristic. See for example this paper and more recently about “characteristic topological invariants” which shows that we can find k-point Green function identities for any m-characteristic. For k=2 (2 point interactions of simplices), we have for m=1 the original Euler characteristic story where g(x,y) is the inverse of the connection Laplacian and is unimodular. Already for Wu characteristic (m=2), the Green function matrix g(x,y) is no more unimodular in general but still holds, where now . If we think of a characteristic as an energy then g(x,y) is a potential energy between the elements x,y of G. Only the first characteristic (Euler characteristic) is a homotopy invariant. The higher characteristics tap more into topology and are topological, meaning invariant only under homeomorphic transformations. Growing hairs to a manifold does not change Euler characteristic, it can change higher characteristics however.

Poetic code: Here is an adaptation of the code from last week with the tadpole graph example. It generates the connection and Dirac matrix, then its inverse and then the Hodge Laplacian.

Generate[A_]:=If[A=={},A,Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]];
Whitney[s_]:=Generate[FindClique[s,Infinity,All]];       L=Length;      T=Transpose;
Connection[G_]:=Table[If[L[Intersection[G[[i]],G[[j]]]]>0,1,0],{i,L[G]},{j,L[G]}];
F[G_]:=Delete[BinCounts[Map[L,G]],1];      S[x_]:=Signature[x];      
s[x_,y_]:=If[SubsetQ[x,y]&&(L[x]==L[y]+1),S[Prepend[y,Complement[x,y][[1]]]]*S[x],0];
Hodge[G_]:=Module[{f=F[G],d,n=L[G]},d=Table[s[G[[i]],G[[j]]],{i,n},{j,n}]; d+T[d]];
K=UndirectedGraph[Graph[{1->2,2->3,3->1,1->4}]];G=Whitney[K];
A=Connection[G];B=Hodge[G];Map[MatrixForm,{A,B,Inverse[A],B.B}]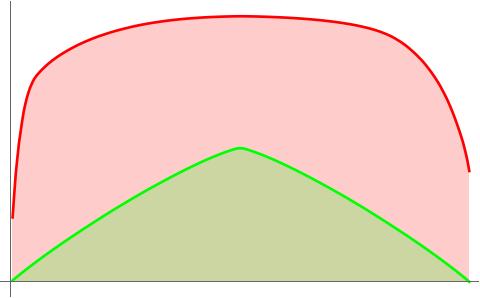

Spectral estimate Update Sunday August 17th: After thousands of experiments, I always see that the spectral sum of the first k eigenvalues of the connection Laplacian is larger or equal than the spectral sum of the first k eigenvalues of the Dirac matrix. It looks as if for all k and that this is sharp.To the right is a typical picture. The red curve gives the sum of the largest k eigenvalues of the connection Laplacian, the green is the Dirac case. At the moment, I don’t see an obvious explanation except that the connection Laplacian has typically a very large Perron Frobenius eigenvalue and that the trace of L is n, while the trace of D is zero. But these experiments could be something for the strong law of small numbers. I know that the number of negative eigenvalues dominates by X(G) the number of positive eigenvalues. If we take a complex with very negative eigenvalues. But so far, with graphs having very negative Euler characteristic, the difference appears even bigger.

Update August 21. I had a bit of a frustrating time with this as the above spectral conjecture appears so easy because L-D is a non-negative matrix with diagonal entries 1. But so far, I could not prove it. It is not true that L-D is positive semi-definite (which means L is larger or equal than D in the Loewner partial order). It can have negative eigenvalues. We know this from linear algebra has eigenvalues 5,-1 even-so it is a very positive matrix. It is also not true that a non-negative matrix is positive in this semi-Loewner situation.