Frenet and Curlicue

If K(t) is a function in a Lie algebra then the Frenet equations Q'(t)=K(t) Q(t), Q(0)=1 defines a path in the corresponding Lie group. We can now use K(t) to define the Frenet path using the equation R'(t)=Q(t). This defines r(t), where r'(t) is the first row of R(t). The Frenet stability problem is to determine the boundedness of the curve r(t).

Last time we have seen that if G=SO(2), and K(t) = k+a sin(mt) with nonzero a, then we have stability if and only if k is not a multiple of m.

There is a discrete analog: look at Q(t+1)=exp(K(t) ) Q(t), Q(0)=1 and then R(t+1) = R(t) + Q(t). Again, this gives a path r(t). The curlicue stability problem is to determine the boundedness of the sequence r(t).

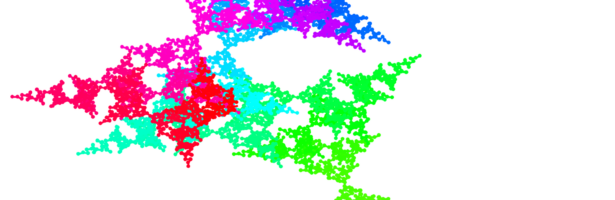
A famous example is if K(t)=at is a real number and Q(t) = exp( a t) . Then Q(t) = exp(i a t(t-1)/2) and we have a Gauss type sum . Plotting this process in the complex plane gives curlicues.

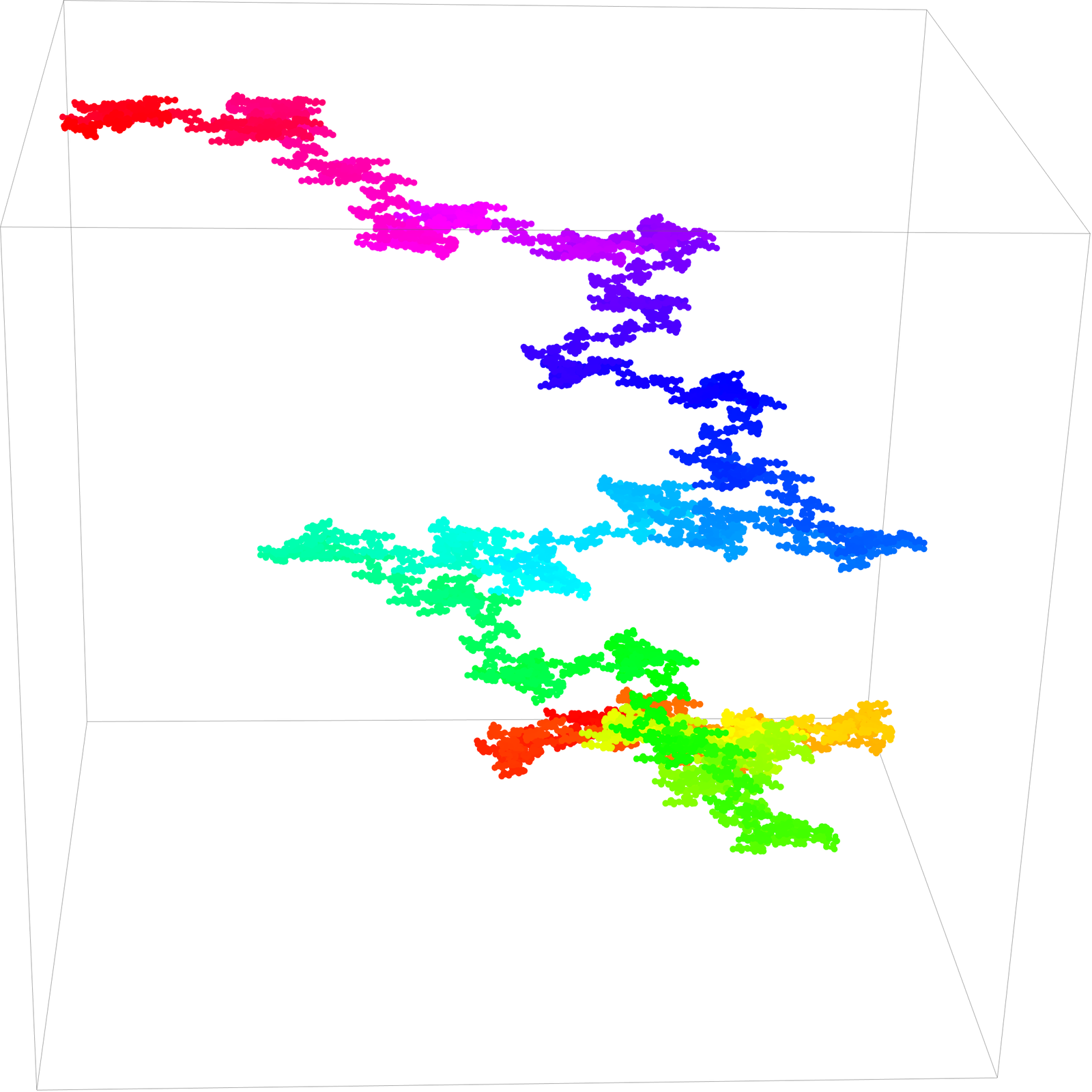
In the talk, I thought that for constant curvature, the 3D curlicues would always be planar. This is not the case. Above right is an example with a constant K in so(3) where curvature is 1 and torsion is 1/100. This is the “discrete analog” of a spiral. What was the thinking mistake? While it is true that the rotation matrix Q(t) rows trace grand circles on a plane this is not the case for the resulting ‘random walk R(t). We should also clarify that the analog of the curlicue situation in the continuum is when the curvature is growing linearly. The picture to the left is such a situation. The case of curvature K(t)=t is the famous Euler curve.

Lets look at two more pictures. The first one is a Frenet situation with curvature k(t) = t(1+sin(t)) the second is a curlicue with irrational curvature square root of 2. In any case, I don’t think the connection between curlicues and Frenet has been done so far even so it is obvious, once you see it. It is similar to see the Hopf Umlaufsatz as a continuum version of the fact that the sum of the complementary angles in an n-gon add up to 2Pi. The curlicue problem could be morphed into a numerical scheme for the corresponding Frenet problem if the step size goes to zero and in the same time also the curvature goes to zero. What happens with is that it becomes more and more random. If we zoom out a curlicue, we somehow keep a minimal quantized radial distance but allow the angle to become smaller and smaller. A truely quantized Frenet situation is if the curvature angle is rational. Already this is an interesting case. We see experimentally that most rational numbers produce unbounded orbits. But there are bounded cases.