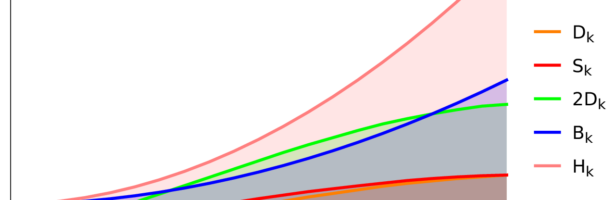
More on Brouwer - Quantum Calculus

If K is the Kirchhoff matrix of a finite simple graph with n vertices and m edges and eigenvalues $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n$ and edge degrees $d_1 \geq d_2 \geq \cdots \geq d_n$ . Define $D_k=\sum_{j=1}^k d_j$ and $S_k = \sum_{j=1}^k \lambda_j$ and $B_k=m+k(k+1)/2$ and $H_k=m+k(k+1)$ . This is $2B_k-m$ . Then the following general inequalities are known (the first 4 inequalities in the following list) or conjectured (the last inequality in the following list):

$D_k \leq S_k$ (Schur’s Theorem, Schur 1923, Horn 1954, this is a linear algebra result)
$S_k \leq 2D_k$ (Knill 2024, Theorem 1 (see in journal), holds for general quivers also with multiple connections)
$D_k \leq B_k$ (follows quickly from definitions for quivers without multiple connections)
$S_k \leq H_k$ (Brouwer’s Haemers, Can be derived from Knill 2024 Theorem 2, for quivers without multiple connections)
$S_k \leq B_k$ (Brouwer conjecture, from around 2006, it is an open problem )

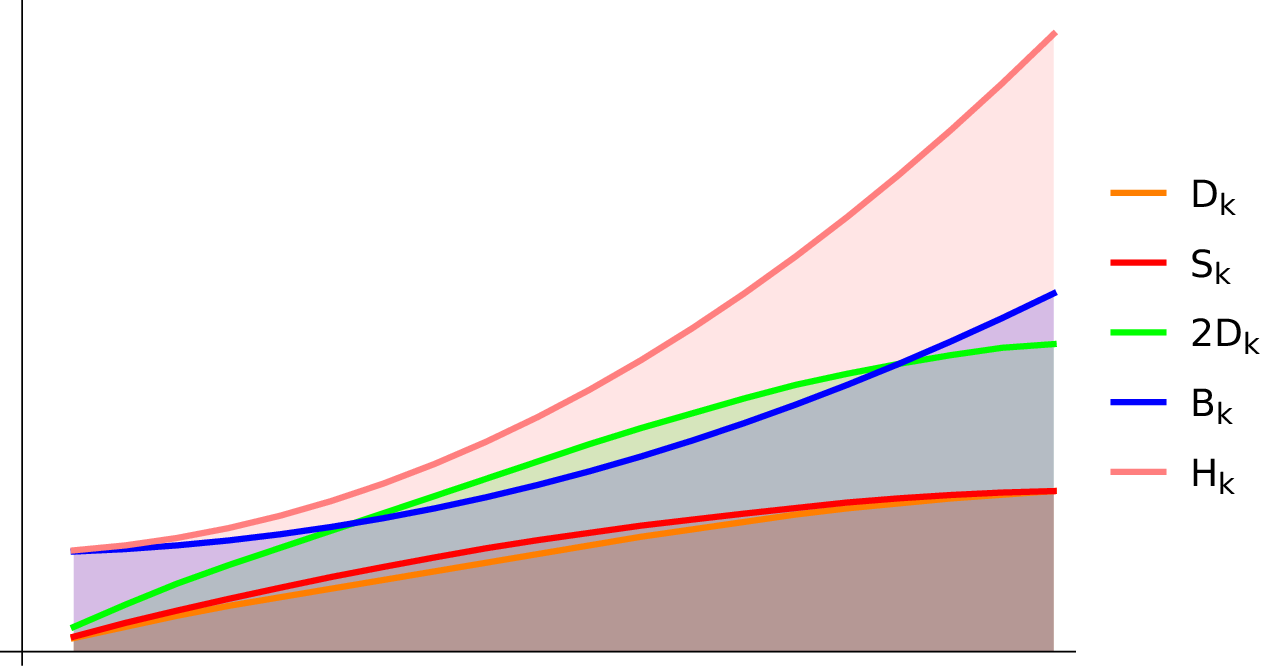
Let us introduce the Brouwer threshold, the smallest number such that for all k<s, the Brouwer estimate $S_k \leq B_k$ holds. Currently we know only s=3 meaning we do not even know $\lambda_1 + \lambda_2 + \lambda_3 \leq m+6$ in general. My snapping trick and seeing that the Brouwer conjecture (if established for a given n) upgrades to graphs with loops (and if adapted with additional redundancy r) to general quivers, shows the following result:

Assume the spectral radius of a graph is smaller or equal than s, then the Brouwer conjecture $S_k \leq B_k$ holds. This is pretty weak but motivates to increase the Brouwer threshold s.

Even so this does not give yet interesting examples, I’m happy now to have been able to use the snapping trick and interlacing.

Author: oliverknill