Pythagorean Triple Day

Yesterday was 9/16/25. You can easily check that it is the only date that is a Pythagorean triple MM/DD/YY. I tweeted

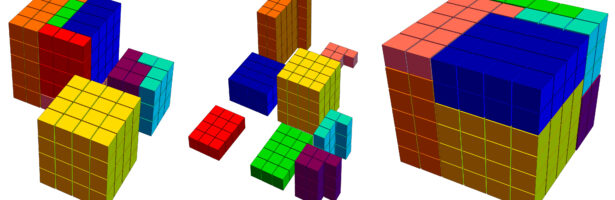
Today's Pythagorean day 9/16/25 is really special. There is no other date of this form. Possible months are 1,4,9, possible days are 1,4,9,16,25. The only pair that produces a square is 9,16.  Check it with  Select[Tuples[{Range[3]^2,Range[5]^2}],IntegerQ[Sqrt[Total[#]]] &]

And made a brief short on youtube about Elkies’s puzzle explaining visually that . If one is asked about the minimal number of puzzle pieces which can explain this using puzzle pieces that are union of cuboids then the answer is 8. The proof (which Noam told me) is quite simple. It involves only the pigeon hole principle and the fact that a cube has 8 corners…. I knew about the puzzle from a while ago, when Noam showed me a 3D printed version a couple of months ago. He got a new, more fancy version. I myself tried (related to the tutorial Math 99 R ) to 3D print my own version. One can produce a printable version in a few lines:

Update: A Wolfram Blog entry.

A[a_,b_,c_]:=Table[Cuboid[{i,j,k}],{i,a},{j,b},{k,c}];
B[a_,b_,c_]:=Union[Flatten[Table[Cuboid[{i,j,k}],{i,a},{j,b},{k,c}]],
                           Table[Cuboid[{a+1,b,k}],{k,c}]];
A1=Translate[A[3,4,1],{0,0,0}]; A2=Translate[A[3,5,1],{6,0,0}];
A3=Translate[A[4,4,2],{0,6,0}]; A4=Translate[A[4,4,4],{5,6,0}];
A5=Translate[B[2,5,1],{5,11,0}]; A6=Translate[B[2,5,5],{0,0+11,0}];
A7=Translate[B[2,2,3],{10,0,0}]; A8=Translate[B[1,3,3],{10,3,0}];
S=Graphics3D[{A1,A2,A3,A4,A5,A6,A7,A8}]; Export["noam.stl",S,"STL"]