Small Dehn-Sommerville Spaces

Dehn-Sommerville spaces are generalized spheres. They share many properties of spheres like Euler characteristic and more generally Dehn-Sommerville symmetries. One can look at the hypothesis that physical space is built in such a way that every small enough sphere is a Dehn-Sommerville space. The structure of such generalized manifolds (realizations of finite abstract simplicial complexes which are Dehn-Sommerville) can be understood better when looking at discrete versions, which encode smooth realizations in Euclidean space. One can ask why. One reason is occams razor. Generalized manifolds with Dehn-Sommerville unit spheres have a simpler structure as they are easier to define than manifolds There is no homotopy in the definition (which is used to define combinatorially what a sphere is).
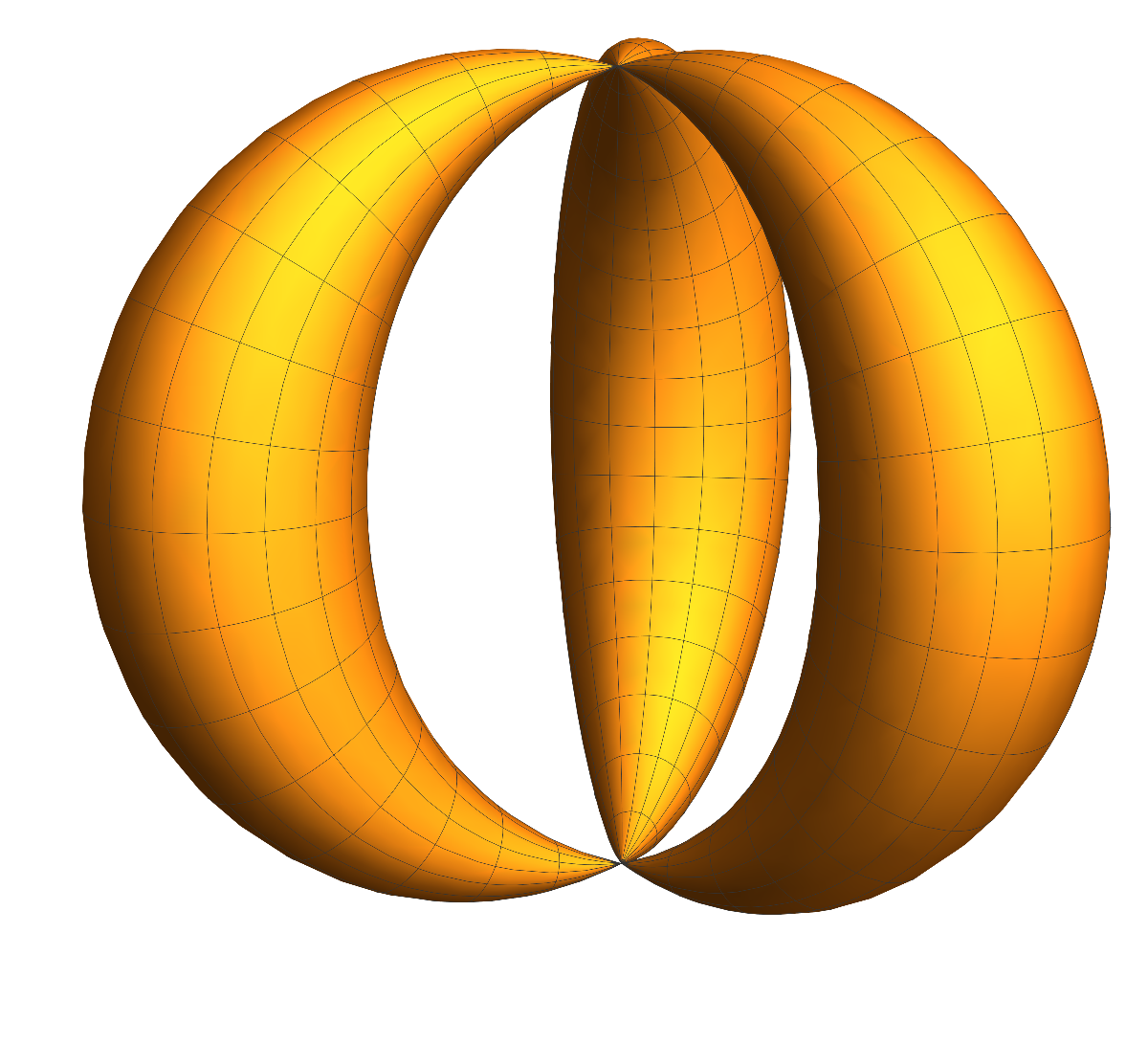
The class $\mathcal{X}$ of Dehn-Sommerville spaces is defined recursively as $\mathcal{X}_{-1} = \{ 0 \}$ and $\mathcal{X}_{d}$ consisting of all finite simple graphs for which the Euler characteristic $\chi(G)$ is $1+(-1)^d$ and for which all unit spheres are in $\mathcal{X}_{d-1}$. There is only one element in $\mathcal{X}_0$, the zero-dimensional sphere. In $\mathcal{X}_1$, all graphs are 1-dimensional manifolds, finite unions of disjoint circular graphs. In dimension $d=2$, things become more interesting. We have the two dimensional sphere, two copies of the projective plane. Then there are varieties, graphs which are not discrete manifolds. One can take such a graph, pick to points and attach a sphere at these two points, the north pole going to the first point and the south pole to the second point. We can also take a projective plane and attach it to the space at one point.
In the first case, when attaching a sphere at two points, we increase the first Betti number by 1 and decrease the second Betti number by 1. In the second case, the cohomology does not change. We see that there are many Dehn-Sommerville space types for $d=2$. To get examples in the case $d=3$, we can take a suspension or a Cartesian product with a one-dimensional space.

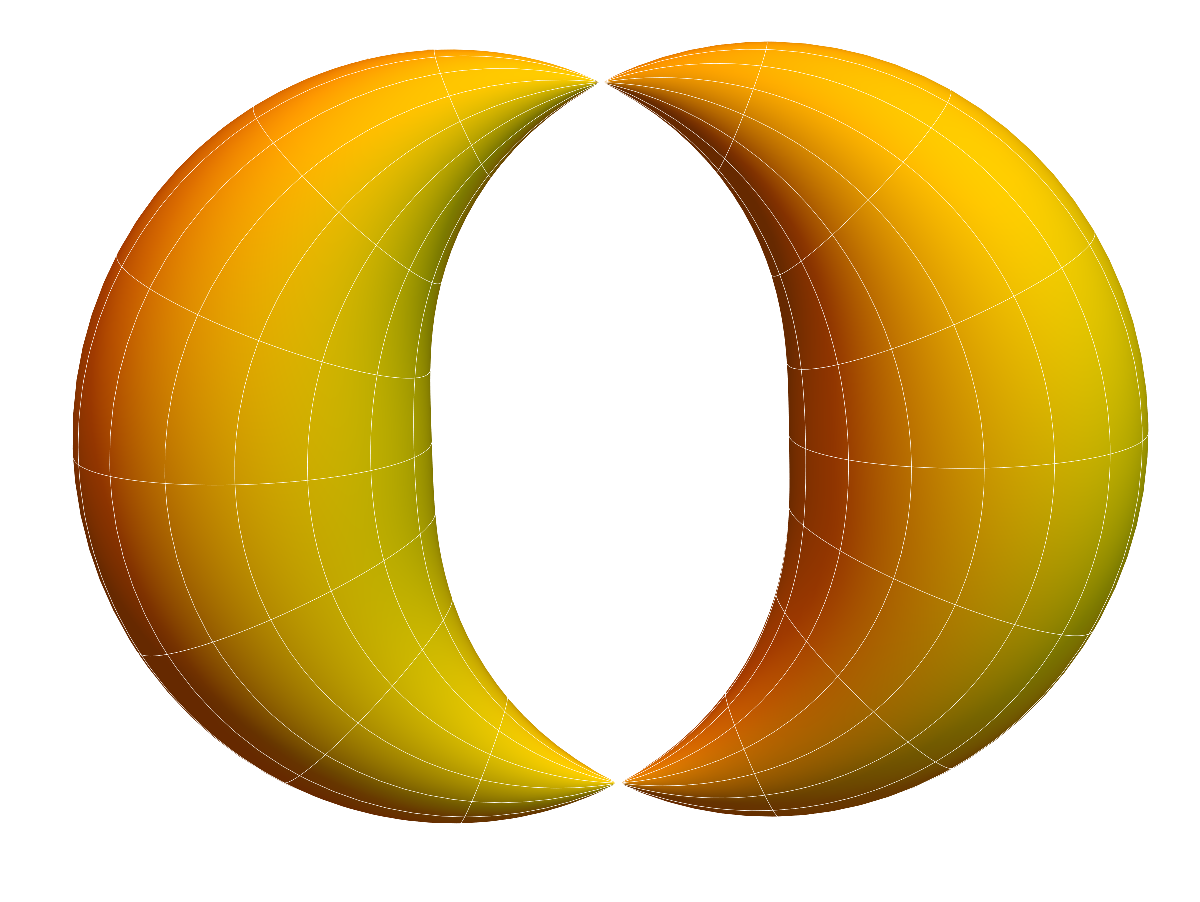
A Dehn-Sommerville space of dimension 2, which is not a manifold. It has the Betti vectors $b=(1,1,2)$ and so Euler characteristic $\chi(G)=1-1+2=2$. There are two points where the unit sphere is not a sphere.	A triangulation of the variety has f-vector (50, 144, 96) and so the f-function $f(x)=1 + 50 x + 144 x^2 + 96 x^3$ which satisfies $f(x-1/2)=96x^3-22x$, an odd function. It is a Dehn-Sommerville grap as any unit sphere is a union of one dimensional spheres (cyclic graphs).

A Dehn-Sommerville space of dimension 2, which is not a manifold. It has the Betti vectors $b=(1,4,5)$ and so Euler characteristic $\chi(G)=1-4+5=2$. There are two points where the unit sphere is not a sphere.	A triangulation of the variety has f-vector (22, 60, 40) and the f-function satisfies $f(x-1/2)=40x^3-8x$, an odd function. In this case, we did not take a Barycentric refinement.