Types of Matrices - Quantum Calculus

Every linear algebra course battles the concept of similarity. We learn that trace, determinant, rank or eigenvalues allow to check whether two matrices are similar or not. For $\left[\begin{array}{cccc}0&0&1&0\\0&0&0&1\\0&0&0&0\\0&0&0&0\end{array}\right]$ and $B= \left[\begin{array}{cccc}0&1&0&0\\0&0&0&0\\0&0&0&1\\0&0&0&0\end{array}\right]$ , all these checks pass but the matrices are not similar. The trick is to look at the rank of $A^2$ and $B^2$ which also must be the same for similar matrices. This allows to decide that the matrices A,B are not similar.

I tought linear algebra Math 21a at the department since 2001, first under the wings of Richard Taylor and Cliff Taubes. I course headed the course Math 21b the last time in the spring of 2018 and just taught a section in the spring of 2023, where I had some time (administrative work when coordinating multi-sectioned courses is substantial) to write youtube shorts summarizing each lecture in less than 1 minute each. During all these years, the text book of Otto Bretscher had been a good resource and it was problems like the above similarity problem which made the book a great asset. In the winter of 2008, I had volunteered to rewrite the solutions for the new edition for Otto’s book. There were many (maybe a 100-200 new) problems but also reshuffled old problems from the older edition. At that time, publishers would reshuffle the numbering so that students have to buy the new edition! It would have been a nightmare to do that all within TeX. So, I wrote first a database of all the problems (the entries of the data base were tex snippets with solutions) and wrote Perl programs (all from scratch of course) to write the solution book for the new edition! Having that database of solutions was actually quite handy when teaching this course for an other 10 years. When teaching it in the spring of 2009 , I had been discussing with Po-ning Chen (now at UC Riverside) whether it is true that the rank pattern is a complete invariant for similarity of matrices. We thought this was true but did not prove it.

When Jessie Pitsillides was interested in writing a senior thesis in the area of linear algebra and especially about matrix factorizations or normal forms, I suggested to look at that problem I had pondered with Poning unsuccessfully. The rank patters of a matrix A are the integers ${\rm rank}(A-\lambda)^k$ . The question is:

Question 1: Are the rank patterns a complete set of invariants for similarity?

Jessie answered it affirmatively and wrote down a detailed proof over the winter break (a longer proof not mentioned in the talk below, the shorter explicit construction came later). At the end of February, we found out that this is already known. It is Corollary 5.17 in the 2012 book of Igor Shafarevich and Alexey Remizov. Of course that was a bummer. But this happens maybe 90 percent of all times, you find something new. The word of mathematics is large and what you see by googling is just a tiny tip of the iceberg. But also looking through books is often not enough and there is lots of work done which does not make it into books.

[P.S. My personal own biggest disappointments in this respect was the rediscovery of the Forest Matrix theorem which tells that the determinant of 1+L gives the number of rooted spanning forests in a graph. Just shortly after my submission to the arxiv in July 2013 I discovered that Chebotarev and Shamis had done that before. Still, there is the satisfaction of not only having distilled the result from experiments but also of having been able to prove it. It does not actually matter whether you were first or not. It is the process that is important. Also, when doing something on your own, you really own it. Its like climbing a tour red point and afterwards learning that somebody has done that before. In that context one also must state that working in a classical area like linear algebra, one has to plan to spend most of the research time with afterwards looking through the literature in order to see whether it has already been found. This certainly happend with the Cauchy Binet generalization I had worked on in 2012-2013 https://arxiv.org/abs/1306.0062. The classical Cauchy-Binet result was proven independently by Cauchy and Binet in 1812, long before matrix algebra had been invented. It is at the heart of that field and making progress in such a fundamental area is difficult because one has competition of more than 2 centuries of mathematics. Millions of people have looked at the classical Cauchy Binet theorem (it is taught in its simplest form as $det(AB)=det(A) det(B)$ in every linear algebra course ever taught on this planet. ]

Getting back to the rank pattern theorem, Jessie managed to get later an explicit algorithm to get from the rank pattern to the Jordan normal form: The rank pattern gives the kernel pattern. Take the discrete derivative of the kernel pattern, which is an integer partition. Then, the conjugate partition gives the structure of the Jordan blocks! I explain this a bit in the movie. While the next theorem appears in the book of Shafarevich and Remizov, the point of the following is on “explicit”, giving a concrete way to get from the rank pattern to the Jordan normal form.

Theorem 1 (Pitsillides) The fact that the rank pattern is a complete invariant for similarity is explicit.

The disappointment of having the theorem already in the literature was not only bad. It prompted to expand the project a bit more. I suggested to look at the counting problem:

Question 2: How many different Jordan form patterns are there?

The answer (which is also in the thesis of Jessie) leads to the combinatorial notion of partitions of partitions. I actually had thought that the answer would be twice partitioned numbers but for n=4, there is the first discrepancy. The twice partitioned number of 4 is 15, while the partitions of partitions number for 4 is 14. The theorem of Pitsilledes is

Theorem 2 (Pitsillides) There are P(n) different Jordan form patterns among n x n matrices.

I myself can claim credit here for the question and some computer algebra assistance for exploring this experimentally, but it is the theorem of Jessie. [P.S. The sequence P(n) is cataloged as A001970.]

While preparing for the presentation below, I looked up a bit more the history and especially why Segre characteristic appears in this context. [I actually mentioned Beniamino Segre (1903-1977) but it also could have been named after his uncle Corrado Segre (1903-1977). Update of May 7: AI claims that Segre characteristic is named after Corrado Segre which actually can make sense as Corrado was more working on quadratic form intersections while Benjamino was more into finite geometry.] In any way, here is a short explanation why algebraic geometers were interested in counting types of Jordan normal forms (despite not mentioning Jordan normal forms!) It belongs to the area of intersection theory. The mathematicians in this area did originally not think about algebra but more about geometry. They wanted to classify intersections of quadrics, something which has been studied since ancient Greece. Think about conic sections for example or the classification of quadrics in dimension n. Given two quadratic forms A,B (symmetric matrices), they define quadrics like $\langle x, A x\rangle=c$ and $\langle x, B x\rangle=d$ . One can look at solutions of $(A-\lambda B)x =0$ which amounts of classifying singularities in the form of tangent points. I myself like to place this more into the context of something which is more familar to me, like multi-variable calculus, especially the topic of Lagrange multipliers. Given two quadratic functions $f(x)=\langle x,Ax \rangle$ and $g(x)=\langle x,Bx \rangle$ , we can ask to maximize $f$ under the constraint of $g=c$ . At such points the tangents are parallel. The Lagrange equations are $Ax-\lambda B x=0$ which mounts to look at $det(A-\lambda B)$ . While A,B are symmetric, we have now a problem for a non-symmetric matrix $B^{-1} A$ . 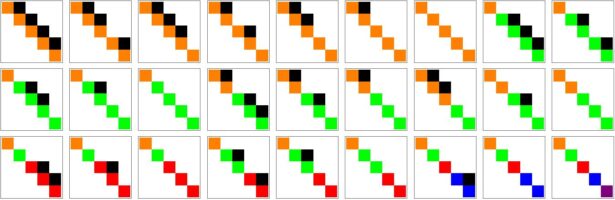One can easily restrict to the case where B is non-singular and then study $det(B^{-1} A - \lambda) = 0$ which is a spectral problem for a in general non-symmetric matrix. The classification of invariants for quadratic forms (meaning that we are intersted in the type of possibilities which can not be transformed into each other by a change of variables) now is the classification of Jordan normal forms for general matrices. It is now understandable why the linear algebra problem has been studied before, before matrices existed. It turns out that the double partitioned numbers already appeared in a publication of 1858 by Sylvester. Historically, Sylvester invented the word “matrix” just before Cayley introduced matrix algebra. Note that the Jordan normal form was stated first only in 1870. The Jordan form classification has to our knowledge not been asked for, even so Sylvester had the double partitioned numbers P(n) mentioned in the context of intersection theory in 1854. Here are the P(5)=27 possible Jordan normal forms of 5 x 5 matrices:

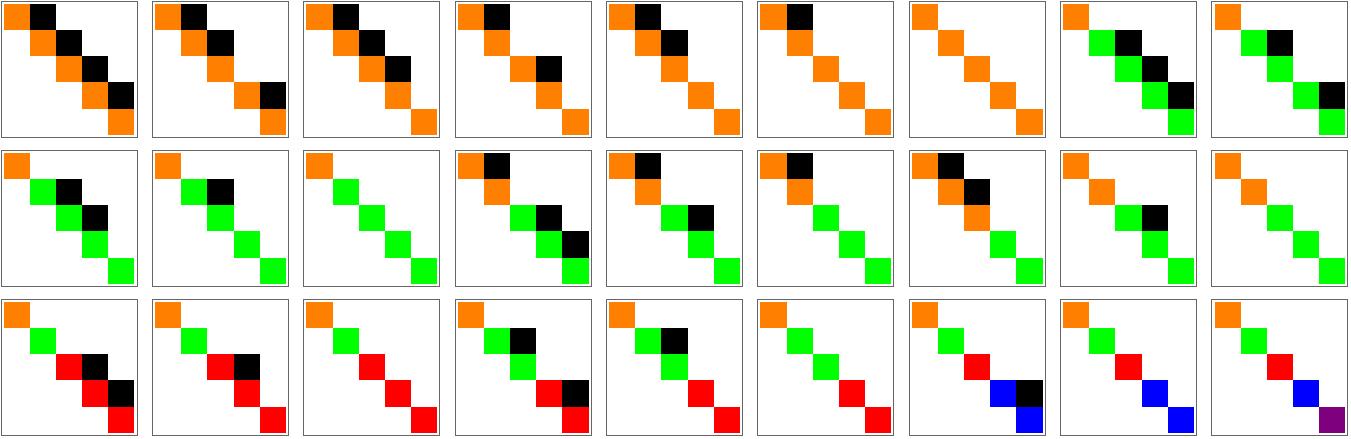
Update May 7, 2025: here is the table which Sylvester compiled in 1854. Sylvester is also known for his law of inertia and that he coined the notion of “matrix”. From the collected work of Sylvester. But it is important to note that no Jordan form matrices appear there as Jordan normal form was introduced only 16 years later by Jordan.

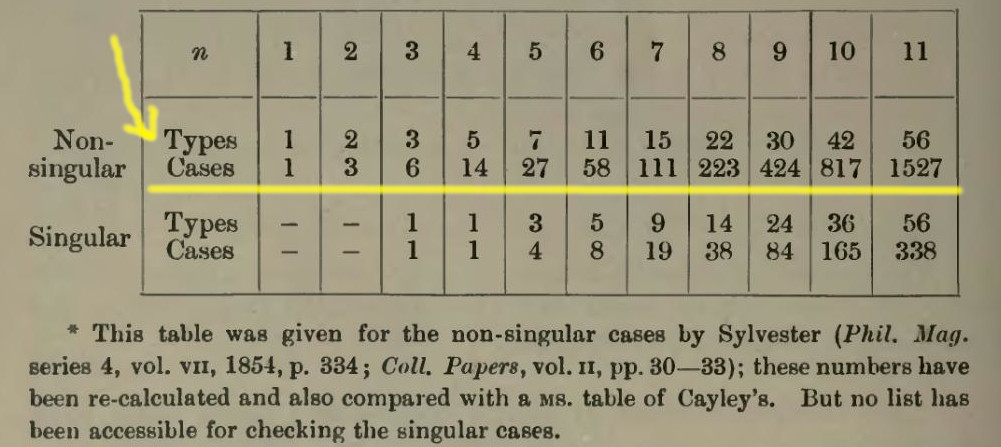
The following table right is in the book of Bromwich from 1903. It refers to a paper of Sylvester. And to the left is part of the work of Sylvester from 1854, a time when Sylvester had been very active.

Author: oliverknill