Ultra finite calculus

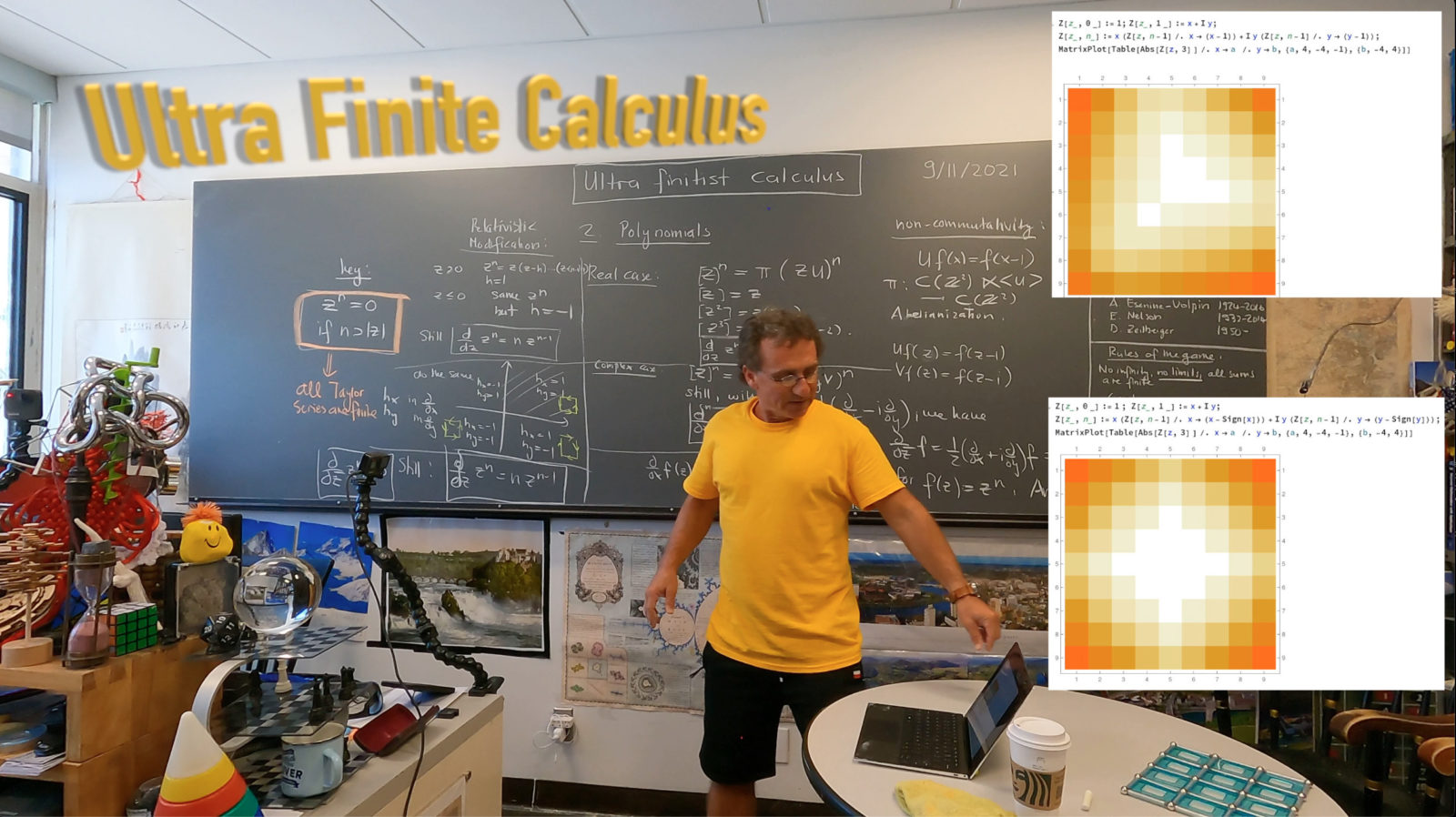
These days, I look a bit at an elementary problem. Deform the algebra of polynomials and derivatives so that all Taylor series are finite sums when evaluated at some point. This is a task which an ultra finitist is interested in. Ultra finitism is a branch of mathematics in which the hypothesis of infinity is not used. Restricting axiom systems can also be seen as part of “reverse mathematics”, a branch of logic which deals with the question which axioms are really needed. I want to keep things very elementary and just looked for now for a polynomial algebra which has the property that is zero if n is larger than the norm of z and such that the usual rules of calculus apply. The prototype is to take as on the positive complex quadrant. With the derivative , the usual identity holds. As usual, the movie also features some drone footage done on the same day. I have some screen shots below. While editing the movie, I experimented with a better symmetric algebra than the one described in the movie.