While walking through the ETH library in Zuerich on Monday, I saw a new book from 2025 by Brian Hopkins called “Hands-On Combinatorics: Building Colorful Trains to Manifest Pascal’s Triangle, Fibonacci Numbers, and Much More”. The ETH library is very nice. I used to work there myself often as a student. The book is beautiful. There are some Selected pages can be downloaded on the website. It is nice for me to see that Cuisenaire visualization sees a renaissance. I had worked in 1981 on a project for the competition “Schweizer Jugend Forscht and had used that visualization technique using the Cuisenaire sticks I had still from first grade. The project Anschauliche Additive Zahlentheorie (164 pages) was typed and with a type writer and pictures were drawn by hand (I think mostly by Felt tip pens or pencils). I recently got back into partitions in the context of constructing manifolds: see Manifolds from Partition: February 2024 (ArXiv) and looked at the ring Colorful rings from Partitions: October 2024 (ArXiv). The former result is easier to teach in a special case, while not mentioning partitions. Like in this handout from my Differential geometry course from Fall 2024. One version to put that result is: if G is a finite abstract simplicial complex that is a q-manifold and f: G -> {0,…,k} is an arbitrary map, then the level set consisting of all x in G having the property f(x) ={ f(v), v in x} that contain {0,…,k} is a (q-k) manifold if it is not empty.
By the way, partitions and partitions of partitions appear also in linear algebra, when counting how many Segre characteristic matrices there are. One can see this in the paper of Jessie Pitsillides with the title “Segre Characteristic Equivalence” that has just been posted on the ArXiv. Jessie had written a thesis “Spectra and Similarity” last spring in which she explored the question of counting similarity classes of matrices.
Here are some panoramas shot while we were in Zurich and below are some pictures (taken also while we were eating in the student mensa),a place where we had been eating for years as graduate students. We then ate later on the Dozenten foyer on the very top of the building. As a student, I had only been very few times there, like to a graduation or some meeting. I don’t remember why, it might have been the high prizes which prevented us to go there, or then that it was simply not allowed without an official reason or that we did not dare. We always ate in the student mensa or then in the Unispital mensa for the doctors of the near hospital (which was very good) and not known at all. You had to go through the hospital and know where it was.
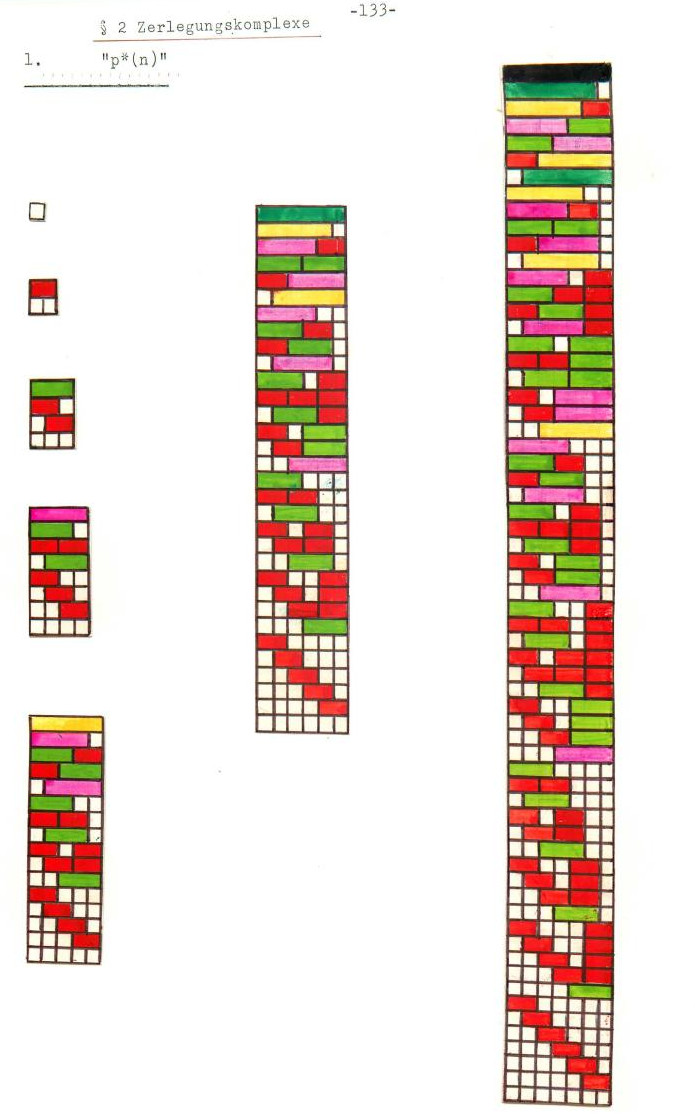
Lets look at a page of Brian Hopkins illustrating the ordered partitions of n. I had called then p*(n) as teenager. I also post my hand-drawn picture of the first few partitions on the right. To the left is the picture from the book from 2025, to the right is my illustration from 1980. The order of the numbers is a bit different I had ordered according to the number of summands and then the order of the numbers. This illustrates the Binomial theorem also better. For p*(4)=8, we have 8=1+3+3+1. There is The order makes more sense than the order given in Hopkins book. The book looks otherwise very nice but I only skimmed through it in the library. I still need to get a copy. On the book cover of the book, unfortunately, plastic versions of the Cuisenaire sticks are displayed. I really think that wooden ones are much nicer.