A bit of a personal health scare this summer (I’m completely fine again) reminded me that we don’t live for ever. This prompted me to rummage through some past initiated work which has never seen the light. One of them was the work on natural groups which still needs to be wrapped up. One of the (nice) dilemmas one has when working independently without a research group pushing for deadlines or polishing things is that math is an infinite playground where one can get lost easily. While floating around in various areas one often gets distracted by new things. For me, when looking at unfinished things, there is one topic I definitely want to make a bit more progress. This is the concept of analytic torsion for graphs. Unlike in a classical setting which relies on (standard) but rather heavy analysis, the case of graphs is completely combinatorial. The topic can be understood and studied by any student who has seen a fewweeks of linear algebra.
Unlike for manifolds or varieties, one can study analytic torsion for general graphs. Every finite simple graph comes with a natural simplicial complex and so also with a natural differential complex. Almost all notions from the continuum can be studied now for general finite simple graphs. One of them is analytic torsion. I got dragged into this in 2012, when working on Cauchy-Binet for pseudo determinants. One of the questions was to understand the pseudo determinant Det of the Dirac operator for graphs where d is the exterior derivative. I noticed (but still can up to now not prove) that for contractible graphs
, the quantity
is a square suggesting that the Dirac operator itself is a square in that case. For general cases, like for example if the fundamental group of the graph is non-trivial, then this number theoretical oddity disappears. This is mentioned in section 8 of my Cauchy-Binet paper. I still believe that the Dirac pseudo determinant somehow is related to Analytic torsion and this hunch has gotten stronger even in that for spheres, there are analogue coincidences for the pseudo determinant of the Dirac operator of spheres. It suggests that there is an even deeper symmetry hidden.
In the summer of 2015, while traveling in Europe, I made experiments with analytic torsion , where
are the form Laplacians, the blocks of the Hodge Laplacian
. I noticed A(G)/|V|=1 for contractible graphs (and more generally for graphs homotopic to 1 like the dunce hat) and looked also at various other cases like discrete manifolds. For spheres, one has either A(G)=|V|/|G| or A(G)=|V| |G| depending on whether the dimension of the sphere is even or odd. [Classically, one takes
. I like to get integer values if possible in our combinatorial setting and taking the square root does not make any sense here. Note that
by McKean Singer which tells
.] The quantity |G| is the volume of the graph, the number of maximal complete subgraphs. The youtube video reports a bit about this. I worked around Christmas of this year (2021) a bit more on it. It turns out that the case of 2-dimensional spheres (which was still not done while recording the video) is quite easy. Remember that a graph is a 2-dimensional sphere, if every unit sphere is a 1-sphere, that is a circular graph with 4 or more elements. Examples are the icosahedron graph or octahedron graph.
So, here is my Christmas theorem (not mentioned in the movie which was done a week before on December 18th):
Theorem: If G is a 2-sphere, then A(G)=|V|/|G|.
Even so, it is small progress only, I like this result very much because it taps into very classical and very beautiful (completely non-technical) mathematics ranging from the mid 19th century (Kirchhoff, Von Staudt or Cauchy) to mid 20th century (like Dirac andMcKean_Singer). So, here is my proof. Of course, I hope to extend this to all d-spheres still. But that requires some more work, as I rely here on situations which only work in 2-dimensions.
Proof: In two dimensions, . By McKean-Singer super symmetry,
, so that
. Now recall that
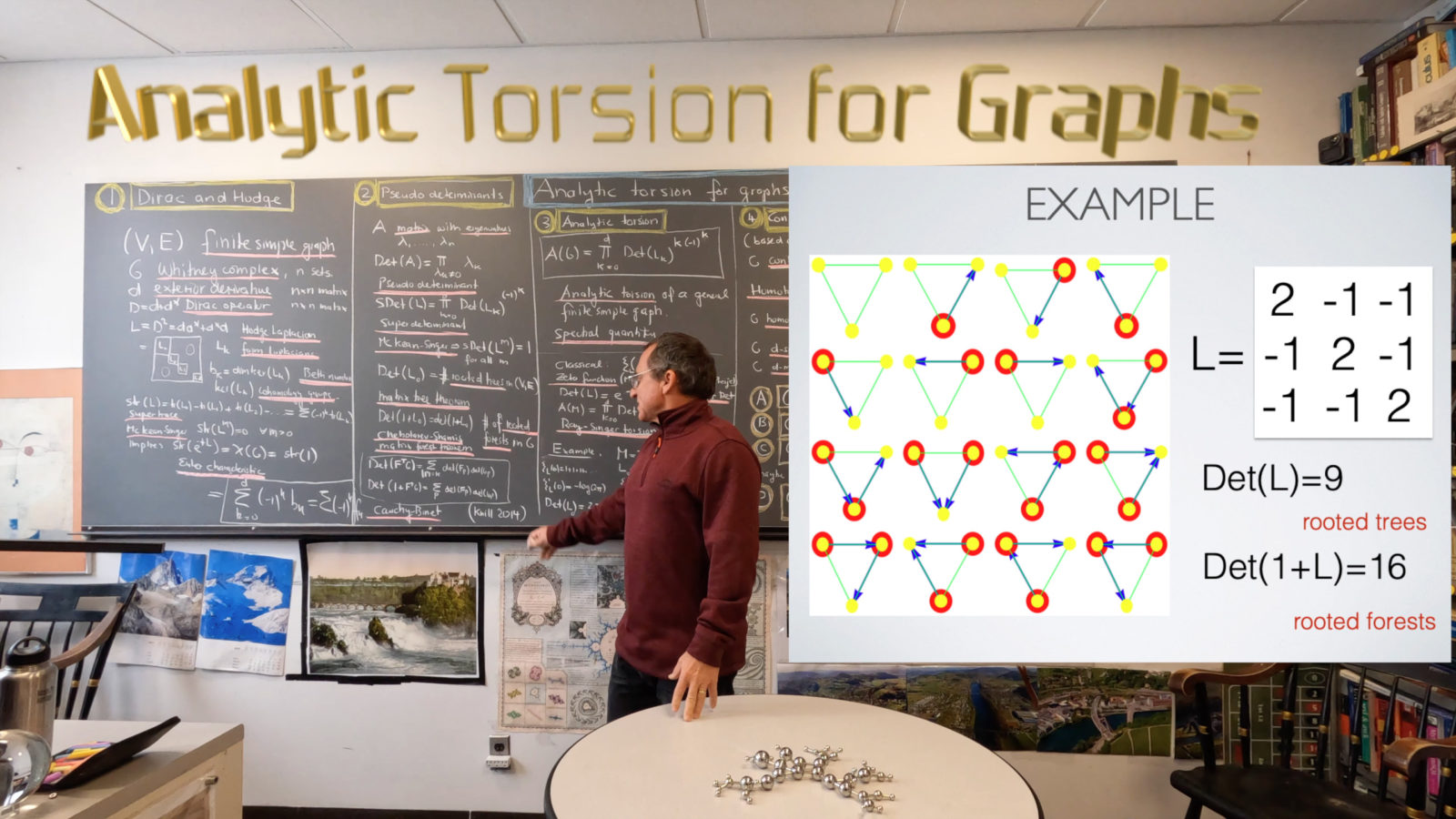
is by the famous Matrix Tree theorem the number of spanning trees in the graph (the matrix tree theory is a direct consequence of Cauchy-Binet). Now comes a beautiful insight from the first part of the 19th century: in modern form it tells that the number of spanning trees in a planar graph is the same than the number of spanning trees in the dual graph. I call it the maze theorem because a two-dimensional maze illustrates that every spanning tree (the walls of a maze) comes with a complementary tree. [Van Staute has first noticed in the first few pages of his book from 1847 that this immediately implies the Euler Gem Formula in two dimensions: the set of edges E of a graph can be partitioned into two sets of size |V|-1 and |F|-1 and |E|=|V|-1 + |G|-1 is just the Euler Gem formula. ] Since
is the number of spanning trees in the dual graph, this implies that
. QED.
Example: If that is not beautiful, I don’t know what is. We combine duality insight from the 19th century to super symmetry insight from the 20th century. To illustrate this, let us just take the Icosahedron graph. We have and
. Now,
. We can check McKean-Singer:
and $6449725440000000^2/(62208000*103680000^3)=3/5$.
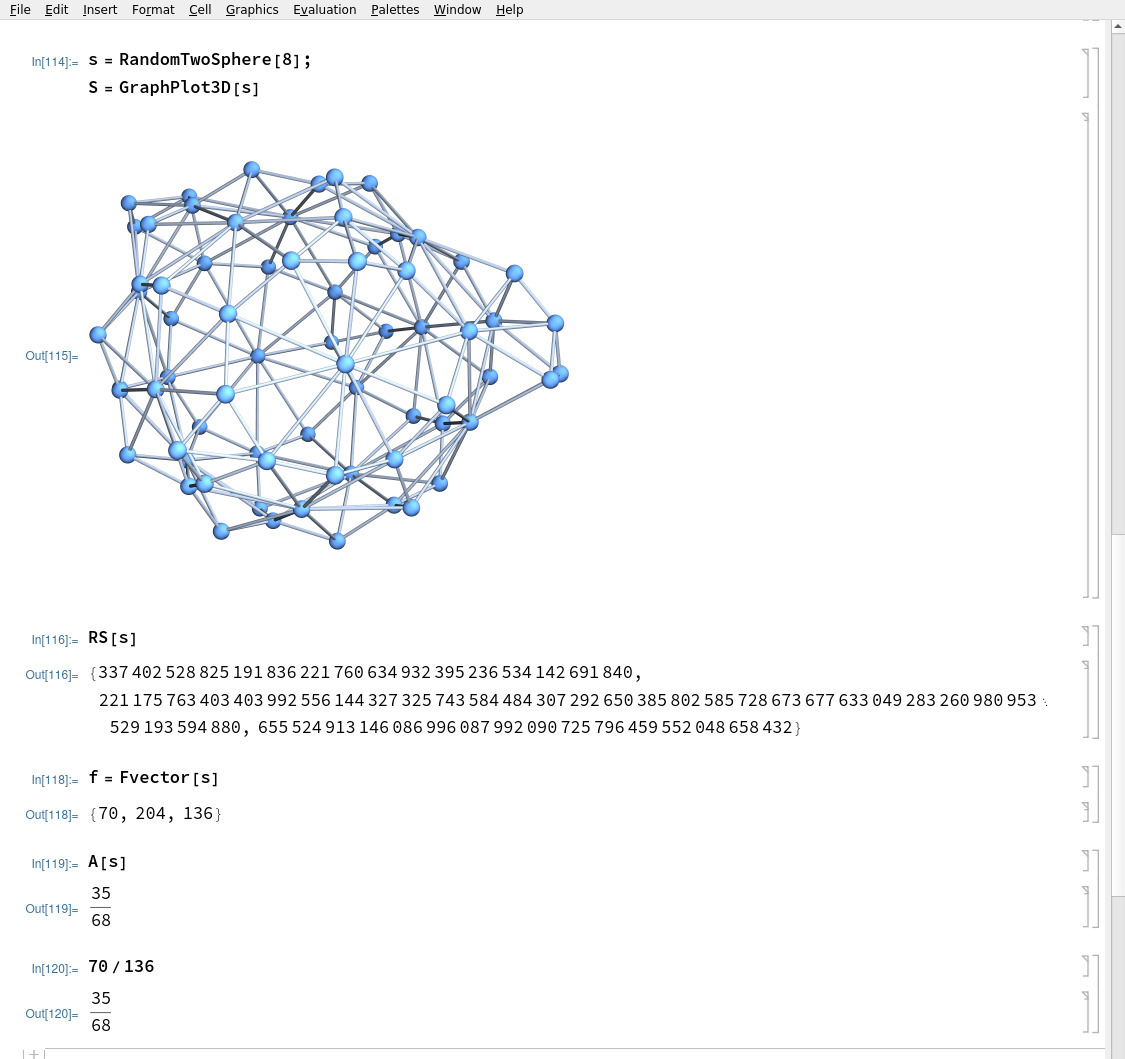
To show an other example, lets just take a random 2-sphere and compute everything. Of course with the computer. You see how large these determinants can become. The Dirac matrix is a 410 x 410 matrix.