More on Analytic Torsion - Quantum Calculus

Having made experiments about analytic torsion A(G) for a graph G=(V,E) in the summer of 2015 and seen that for contractible graphs A(G)=|V|and that for odd spheres A(G)=|V| |V’| and for even spheres A(G)=|V|/|V’|, I had not seen how to prove this then and moved to other mathematics like connection calculus. This winter I returned to the subject. And there was a break through after understanding that analytic torsion is just the super determinant of the Dirac operator D. If $L=D^2=(d+d^*)^2$ is the Hodge Laplacian D which is a block diagonal matrix with entries $L_0,L_1,\dots,L_r$ where $L_k = d_k* d_k + d_{k-1} d_{k-1}^* = D_k + D_{k-1}'$ , then analytic torsion is $A(G) = \prod_{j=0}^r Det(L_k)^{(-1)^{k+1} k}$ , where $Det$ is the pseudo determinant of the matrix. I had been puzzled until around new year why that power k is there. One can not take it away, because McKean-Singer super symmetry tells that the super determinant $SDet(L) = \prod_{k=0}^r Det(L_k)^{(-1)^{k+1}} = 1$ for all graphs. But why take the k’th power of $L_k$ and not say the $k^2$ ‘th power? The reason is that analytic torsion telescopes to the Super determinant of the Dirac operator. This is defined as $SDet(D) = \prod_{k=0}^{r-1} Det(D_k)^{(-1)^{k+1}}$ which is of course the same than $\prod_{k=0}^{r-1} Det(D_k')^{(-1)^{k+1}}$ . 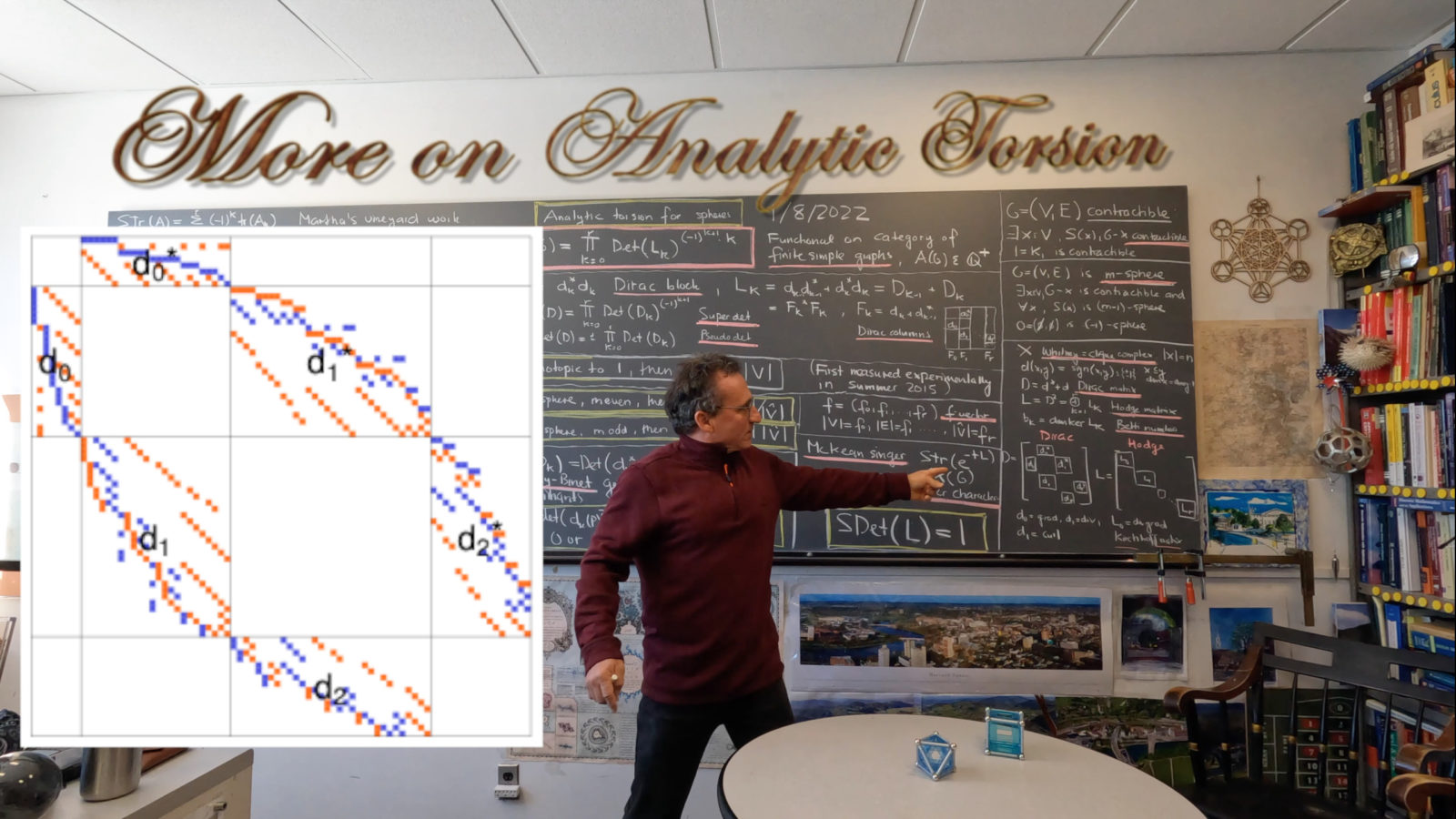The Dirac blocks $D_k$ and $D_k'$ are of course essentially isospectral (which means isospectral up to zero eigenvalues) and also $L_k$ is essentially isospectral to the direct sum of $D_k$ and $D_k'$ . While obvious, this became clear to me only this winter: if $F_k$ is the Dirac column block belonging to the columns of the k-forms, then by definition $L_k = F_k^* F_k$ and now comes the kicker (an exercise for a course like Math 21b (intro linear algebra) but simple things are often hard to see: $F_k^* F_k$ is a matrix of the same size than the Dirac operator D or the Hodge operator L but has only the two blocks $D_k$ and $D_k'$ . Now, the minors of $D_k$ have geometric interpretation as trees! Before seeing this I had spent a couple of days during the early winter break between Chrismas and new year to find a geometric interpretation of the minors of $F_k$ and especially then of then meaning of $Det(L_k^k)$ . The k’th power really does not make geometric sense at first. It was such a relieve to see the torsion definition identified just as the super determinant of the Dirac operator. Dirac was obsessed with beauty. I myself am only really getting interested in things which are simple. Now torsion is really simple and can not be more beautiful:

KEY LEMMA : A(G) = SDet(D) for all graphs

This makes it a much more natural. 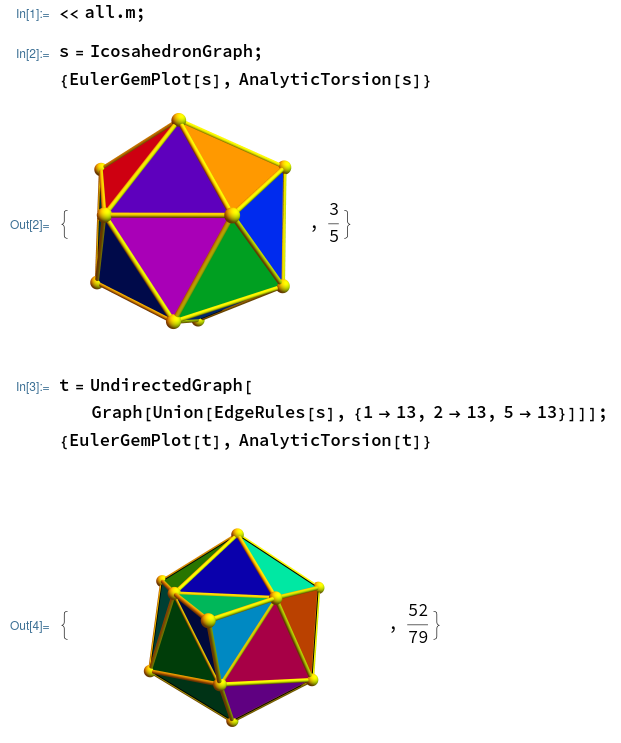As pointed out in the video, I needed there some literature help and especially some linear algebra treated by Gelfand, Kapranov and Zelevinski who introduced determinants for chain complexes. It needs more insight to prove then the statements about analytic torsion. The key is Cauchy-Binet for pseudo determinants. This is the result I’m most proud about as it is a result at the very heart of linear algebra. It immediately implies both the matrix tree theorem and the Chebotarev-Shamis matrix forest theorem identifying the Fredholm determinant of the Kirchhoff matrix as the number of rooted spanning trees in G. Now, one can interpret A(G) as a statement about trees. It will boil down to a statement that for spheres or contractible graphs there is a balance between even spanning trees and odd spanning trees and that A(G) counts the relation between even rooted spanning trees and odd rooted spanning trees. It is important to realize and appreciate that analytic torsion A(G) is a fragile invariant. If you take a 2-sphere like an Icosahedron for example and add an other vertex in a triangle connecting it to the triangles, one considers this in topology usually a local refinement of the triangulation. This changes the torsion:

Author: oliverknill