Brouwer Conjecture - Quantum Calculus

One of the most amazing formulas in linear algebra is the Hadamard first variation formula which tells how an eigenvalue changes if the matrix entries are changed. Take a symmetric matrix K and perturb it as K+t E, where E is an other symmetric matrix. How do the eigenvalues change? To see this, just differentiate $K v = \lambda v$ . It is $K' v + K v' = \lambda' v + \lambda v'$ and assume the eigenvector is normalized $\langle v,v \rangle=1$ so that $\langle v',v \rangle=0$ . Taking the inner product of the previous equation gives $\langle v, K'v \rangle + \langle v,K v' \rangle = \langle v,\lambda' v \rangle + \langle v, \lambda v' \rangle$ . This can be simplified, using K’ = E, <v,v>=1 and <v’,v>=0 and that $\langle v,Kv' \rangle=\langle Kv,v'\rangle=0$ gives $\langle v,Ev \rangle = \lambda'$ . This is the Hadamard first variation formula. In the case of a rank 1 perturbation, where E is the projection onto the k’th coordinate, the formula gives $\lambda'=v_k^2 \geq 0$ . It makes sense of course: if you increase a diagonal entry of a matrix, the eigenvalues should increase. Now, if you take t=1, you have added 1 to one of the diagonal entries the trace increases by 1. So, during the perturbation, all of the eigenvalues can only increase by maximally 1. Can we use the method for a more general Brouwer Conjecture telling: For a quiver with n vertices and m edges (including loops) and redundancy r the eigenvalues $\lambda_j$ (ordered in decreasing order) satisfy $\sum_{j=1}^k \lambda_j \leq m+r+k(k+1)/2$ for all $1 \leq k \leq n$ ? For graphs without multiple connections (r=0), it is the Brouwer conjecture $\sum_{j=1}^k \lambda_j \leq m+k(k+1)/2$ for all $1 \leq k \leq n$ . The simple interlace result works with adaptation only. (See my presentation from Friday). The Brouwer inequality for k=1 follows already from $\lambda_1 \leq d_1+d_2$ which is the Anderson-Morely inequality. The reason is that $d_1+d_2 \leq m+1$ which is sharp if a graph is a tree with two connected vertices of degree $d_1,d_2$ and all other vertices are leafs. We have however $\sum_{j=1}^k \lambda_j \leq m+k(k+1)/2$ as long as k is larger than the spectral radius. This should show the conjecture if $m$ is larger than the square of the spectral radius. I will comment on this next weekend.

Perturbation theory of operators and especially self-adjoint operators has been pioneered by Franz Rellich (1906-1050). He was besides Siegel the second PhD advisor of Juergen Moser. His PhD dad was Richard Courant, who was a pioneer too in spectral theory. Moser married Gerturde Courant, the daughter of Courant. A bit more connection for me personally: Rellich’s sister was married to Bartel van der Waerden, who was teaching at the university of Zuerich. As a student, I myself saw once a talk of Van der Waerden in Zuerich about the history of quantum mechanics. Van der Waerden has a daughter Elisabeth van der Waerden, who had been teaching at the Kantonsschule Schaffhausen and who is a friend of our family. Back to Rellich: he seems have been the first to realize that if one has a one parameter family of self-adjoint real matrices that depends smoothly on the parameter like K(t) = K + t E, then the eigenvalues can be labeled so that that they are smooth functions of the parameter. This is absolutely non-trivial given that collisions can occur and that the second Hadamard perturbation formula involves differences of eigenvalues $\lambda''(t) = 2 \sum_{i \neq j} \frac{ \langle v_i(t), E v_j(t) \rangle}{\lambda_i-\lambda_j}$ which is singular when two eigenvalues collide.

In the case of graph theory this is very interesting already because it tells us what happens if we add a loop to a vertex. It increases the eigenvalues but only by maximally 1 and even if we take the sum of the first k eigenvalues, the sum only maximally increases by 1. This brings us to the Brouwer conjecture: $\sum_{j=1}^k \lambda_j \leq m + k(k+1)/2$ . If we have a quiver for which this inequality holds, then it also holds after adding a new loop. So, it is would be enough to prove the Brouwer conjecture for simple graphs, it then upgrades to quivers. Can we use induction on graphs, then we can get to principal submatrices of the Laplacian if we remove a vertex as long as we add loops to the neighbors. This was the mechanism for the proof of the upper bound inequality $\lambda_k \leq d_k + d_{k+1}$ , where $d_k$ are the vertex degrees of a quiver (but everything was ordered backwards with the smallest eigenvalue being the first one). Doing the proof in a larger class of quivers was easier. In the case of general quivers (graphs allowing multiple connections and loops), the Brouwer conjecture is $\sum_{j=1}^k \lambda_j \leq m +r + k(k+1)/2$ , where r is the redundancy, the number of excess edges that can be removed without affecting whether two vertices are connected or not. Also this estimate should be sharp. Here is a recording from Friday, when I still thought that simple induction could work. But this does not work as simply. I will certainly come back to this problem again. Unsolved problems are attractive.

In any case, the Brouwer conjecture is intriguing because it does not involve the vertex degree sequences like $\lambda_k \leq d_k + d_{k+1}$ (if the $\lambda_k$ and $d_k$ are ordered in a decreasing manner and $\lambda_k \leq d_k+d_{k-1}$ if the eigenvalues and degree sequences are ordered in an increasing manner (as in Riemannian geometry). The Schur inequality (also known as Schur-Horn inequality) gives in the case of decreasing eigenvalues $\sum_{j=1}^k \lambda_j \geq \sum_{j=1}^k d_j$ . (I’m more used to increasing eigenvalues, where the Schur-Horn inequality gives a lower bound $\sum_{j=1}^k \lambda_j \leq \sum_{j=1}^k d_j$ . Both cases follow quickly from interlacing. In the “decreasing eigenvalue case”, delete the row and columns containing the smallest diagonal entries $d_{k+1}, \dots d_n$ (this is what is covered for example in the book of Brouwer and Haemers). In the “increasing eigenvalues case”, delete the row and columns containing the largest entries. It is tempting to place a vertex degree estimate between $\sum_{j=1}^k \lambda_j$ and $m + k(k+1)/2$ (again ordered in a decreasing manner as Brouwer’s conjecture demands). My estimate $$latex \lambda_k \leq d_k + d_{k+1}$ (which is the statement in the decreasing case) gives for the sum $S_k=\sum_{j=1}^k \lambda_j \leq (2\sum_{j=1}^k d_j )-d_1-d_k$ . 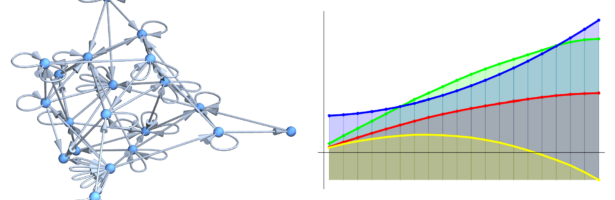We need better than that because the Brouwer conjecture bound competes with the degree estimate: Here is an example. We see a graph (with some loops) to the left. To the right we see (in red) the sequence $S_k$ , which is the cumulative spectral sum. The blue concave up bound is the sequence m+k(k+1)/2 the Brouwer-Haemers conjecture. The green bound is what my theorem from 2024 uses the degree data. Yellow is the known Brouwer-Haemers lower bound (a short proof had been covered in my paper of 2024 too). The graphics has been produced assumes decreasing eigenvalues (as in the Brouwer conjecture). The example shows also a difficulty of the Brouwer conjecture. The vertex degree estimates as well as the spectral functions are concave down, while the Brouwer estimate m+k(k+1) is concave up as a function of k. And we see that the bounds in general compete. This implies that an improvement over the degree estimate is needed in order to prove the Brouwer conjecture, if one wants to use vertex degree sequences at all. Anyway, the only new takeaway so far is that the conjecture upgrades for all quivers with the modification of adding the redundancy r to the right (Provided the original Brouwer conjecture for graphs works). The “snapping trick” is helpful too in the class of quivers (used with the vertex of maximal vertex degree) which produces again a Kirchhoff matrix of a quiver then just gives an estimate of $\sum_{j=2}^k \lambda_j \leq m+k(k-1)/2 = m-k$ so that if $k> \lambda_1$ we are fine.

Author: oliverknill