The first part of this year 2020 (actually already a bit in December), I had still been a bit on “vacation from discrete mathematics” and worked more on pure classical Riemannian geometry. There is a more technical miniblog entry on my website. Note that the preprint contains errors. It clearly indicates that am working out way of my comfort zone, when working in Riemannian geometry, but it is nice for a while to feel again like a student and learn and also feel awful about making mistakes. I’m currently working still on a new draft and always keep the latest version here. [PDF].
The project deals with a new curvature which when integrated often appears to agree with Euler characteristic. I was convinced 2 months ago that the integral of this curvature would be Euler characteristic, but that would have been too good as it would have solved the famous Hopf sign conjecture. I then computed with the 8-manifold SU(3) and saw that the quantity is positive even so the Euler characteristic is zero (as for all Lie groups). SU(3) is one of the super stars among Lie grups as it is the gauge group of the strong interaction and the major player of the “Eightfold way” as the Meson and Baryon octets are related to the representations of this group. Lie groups are great examples for Riemannian geometry because one has to compute the curvature tensor only at one point and by homogeneity has it everywhere. The relation between algebra and geometry there has been especially developped in the 1970ies, there is especially a paper of Milnor from 1976 which is still now a great reference when interested in the Riemannian geometry of Lie groups. The computations of the Gauss-Bonnet-Chern integrand or sectional curvatures is for Lie groups explicit using the adjoint representation. Lie groups always have zero Euler characteristic by Poincaré-Hopf and the fact that they feature non-vanishing vector fields. It worked nicely for the 6-manifold SO(4). To my dismay, the new invariant was positive for SU(3) while the Euler characteristic is zero. [The group SU(3) is beautiful and also a nice 8-dimensional Riemannian manifold. One of the first who suggested quarks was Murray Gell-Mann. When I came to Caltech in 1993, the year he retired there, there was behind the Sloane lab building still a parking lot with his name written on, I would see it every time, I would leave the building from the back to grab some coffee in the Red door cafe (which I think is now at an other location). The math building has recently called the Linde Hall of Mathematics and Physics as one can learn here.]
[ Update of May 30, 2020: The SU(3) discrepancy was only the beginning of retractions. I then thought that the functional is independent of the metric, which turned out to be wrong, even the independence of the coordinate systems is not true. The later is not a big issue as theoretically, always the coordinate invariant version was considered and an integration over a smaller dimensional part in the tangent space is enough to get the coordinate independent version. Somehow it was actually good to look at the discrete sum, as this has a chance to be computed. Computing integrals over large dimensional symmetry groups are just tough. I’m still working heavily on making amendments. See the local blog on my website which is easier to edit than wrangling with a visual editor in this wordpress content management system. One of the goals is to actually compute the coordinate independent gamma value for SU(3). ].
[Update June 12:]Towards the result
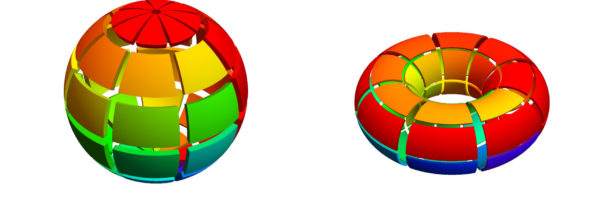
If we are at a point x in an even dimensional Riemannian manifold M, we can introduce normal coordinates there. This means that the coordinate axes are perpendicular to each other and that the coordinate axis are nearby given by geodesic lines emanating from the point. We are all familiar with that ,when looking at maps of the earth where the sphere is the Riemannian manifold. If we are at a point different than the poles, we can chose north and east direction as a basis for example. On the poles we can use east and west as coordinate basis. The geodesics extend to grand circles on the sphere. In a 2d-dimensional compact Riemannian manifold we have 2d coordinate axes. We also can write the tangent space as a product of d 2-dimensional coordinate planes. Two dimensional sub-spaces are very intuitive as we are familiar with drawing on two dimensional paper for example. We also have a very good intuition about sectional curvature, which is the curvature of the surface obtained by shooting out light along a two-dimensional plane in M. Of interest are now averages of such sectional curvatures or products of them. For example, we can look at the average of all sectional curvatures at a point. This is proportional to the scalar curvature. Integrating this over the entire manifold gives an important notion in relativity, the Hilbert action. Of interest can also be the average value of sectional curvature products 
Motivated by probability theory one can see the product of curvatures as an index expectation. I had in February 2020 boldly guessed that this K always integrates up to Euler characteristic. If you look at the two papers here and here, the claim is actually not that bold at all, but very natural. Of course, I was very excited because if this were true, then one of the major conjectures in Riemannian geometry, the Hopf conjecture could be in reach. After looking at few examples and also numerically computing K in “non-Lie group” or “non-product” situations, the claim appeared to be reasonable and in mid March, two months ago thought to be able to prove it. I even recorded slides and rehearsed a blackboard talk at home. It looked good. But then I computed K for SU(3), one of the most famous Lie groups and found it to be positive despite the fact that the 8-manifold SU(3) has zero Euler characteristic. [[ Update May 30: this orthotop part might actually not matter as there were aother mistakes. Over the next few weeks it became clear what was wrong. I had assumed naively that one can chop up any Riemannian manifold into orthogonal pieces. This would follow for example, if one can partition M into cuboids or smooth distortions of cuboids. Of course, one can partition any smooth manifold into simplices, so it should be a piece of cake to make this also with cuboids. Especially as the existence of conformal coordinates in two-dimensions makes it obvious in the 2-dimensional case and because the obvious manifolds one can think of like for product manifolds, tori or spheres things work in arbitrary dimensions. It must follow now that SU(3) can not be chopped up into small orthogonal rectangular pieces. This reminds of Hilbert’s third problem asking whether two polyhedra of equal volumes can be cut into polyhedral pieces so that one can reassemble each from the pieces of the other. Max Dehn, a student of Hilbert then solved the problem and answered it negatively in three dimensions and higher. The analogy is not so far as this is also a situation where the cutting works in two dimensions but not in higher dimensions. So, in some sense the difference between the integral of K over M and the Euler characteristic plays the role of a Dehn type invariant, hence the title of my paper “A Dehn type invariant for Riemannian manifolds”. Maybe instead of repeating the results stated there, just check out that paper. I will post later this week some slides.
Relation with quantum calculus
Now, this is a quantum calculus blog and Riemannian geometry is quite a classical topic, far removed from anything quantum. But this is only so when looking at it superficially. There are many techniques which have been developed in Riemannian geometry which are of quantum origin. An example is the Witten deformation approach to Morse theory which is a semi-classical approach and so very quantum mechanical in nature. An other example is the Patodi proof of the Gauss-Bonnet-Chern result which uses creation and annihilation operators known in quantum field theory. There are other relations if one thinks at relativity: the global point of view of seeing a Riemannian manifold as a global entity is beautiful and pure but it is not compatible at all with relativity and causality. If we look at some quantity of space like curvature K(x) (which might be related to the presence of mass or energy at that point), then the quantity K(x) and K(y) for separated x,y can have no relation with each other at a specific time. This plays a bit against the pure Platonic point of view of Chern who looked at things coordinate independent and who was a master to build proofs in such frame works.
[By the way, I feel lucky to have been introduced to Chern once at ETHZ during a conference. Moser, my undergraduate advisor, who had collaborated with Chern and knew him well, introduced him once to me and said: “This is Chern, one of the greatest geometers of our time”. I of course was flattered as I was just a student and could shake hands with Chern, who was as I can confirm, a very friendly and charming person. It is not by accident that Moser and Chern were compatible as both had a bit of that “twinkle in the eye” meaning they were content with how things were, both had not to prove anything any more, and also shared a bit of good humor. One can see some of the humor of Chern even in his writings. Related to the topic of chopping up manifolds, Chern once wrote in a Monthly article that “chopping up a manifold bears the risk of killing it”.]
Now, I must say that Chern’s proof of the Gauss-Bonnet-Chern theorem is still a bit of magic for me. I can intuitively grasp better a combinatorial proof in which the manifold is chopped up and where the gluing of different pieces is analyzed. This is the Allendoerfer-Weil approach. It can also be seen somehow as a quantum approach in which one considers a manifold to be a discrete entity made of simplices where each simplex is of Planck length. It is quite reasonable that any quantum approach to gravity one has to course grain or quantize space too. As there is also a time evolution involved an even better model is to see the manifold as a CW complex where the order of the elements matter. I personally can not see how a global space-time manifold quantization ever will work in a possible theory of quantum gravity. This is leading a bit too far away from the underlying geometry but chopping up a manifold into simplices and analyzing the curvature in each part then glue things together is very elegant too and I disagree here with what probably most of differential geometers think. One of the advantages of chopping things up is that one use local methods, then just needs to analyze what happens if the local small parts are glued together. Now this looks very technical, especially if one looks at the Allendoerfer-Weil approach which built on Tube methods put forward by Herman Weyl. [ Also a bit as a side remark, the early part of the 20th century had been still very exiting mathematically in that many mathematicians were also polymaths, who worked in completely different areas. In the centuries before this had still been the norm as Riemann, Gauss or Euler showed, but mathematicians like Andre Weil or Herman Weyl or Carl Ludwig Siegel were fluent in various parts of mathematics André Weil for example was not only a giant in algebraic geometry and number theory he worked also in Riemannian geometry. It is extremely rare in modern times that people work in completely different major mathematical areas.] But actually, the proof is not technical at all if one does use the right tools.
About Poincare Hopf
Going back to the analysis of curvature in Riemannian geometry, the chopping approach allows to bypass differential forms or tensor analysis which both can produce quite a bit of technical overhead. All is needed is a bit of multi-variable calculus. This magic is possible because of Morse theory. Morse theory wonderfully tames any pathological cases. Unlike the analytic category, the $C^\infty$ category can be very complicated. Singularities coming from critical points of smooth functions can have complicated structures. This all magically simplifies when assuming a Morse condition. The singularities are then all nice and dandy and the Poincar\’e-Hopf indices then are either 1 or -1 at a critical point depending on whether the Morse index m(x), the dimension of the stable manifold at such a hyperbolic critical point is even or odd. Now, taking a probability space of Morse functions produces a curvature. No tensor analysis needed, no differential forms are needed, no vector bundles are needed. It is just Fubini’s theorem assuring that integrating over the probability space of Morse functions and integration over the manifold can be interchanged. Now, if we have chopped up a manifold, we get Riemannian polyhedra. They especially have a boundary and lots of critical points are in general on the boundary. Actually already in the simplest case of a triangle equipped with a probabilithy space of Morse functions coming from linear functions in an ambient space (the plane for example), the curvature is located on the vertices and given by the dual angles $\pi-\alpha,\pi-\beta,\pi-\gamma$. Summing up these curvature gives $2\pi$. The sum of angle formulas is the simplest known Gauss-Bonnet incarnation. Now what happens with Gauss-Bonnet-Chern is that via a Nash embedding, we can always chose a global probability space for the entire manifold M. If we can show that the curvature glue disappears after joining together individual chops of the manifold, then the proof of Gauss-Bonnet-Chern is extremely simple. Actually, we do not even have to glue them. The Gauss-Bonnet-Chern theorem is essentially a tautology if we accept that the Gauss-Bonnet-Chern integrand comes from a Nash embedding in an ambient linear Euclidean space equipped with linear functions (and of course if we accept Poincaré-Hopf.) Already Morse knew that almost all such functions induce Morse functions on M. Well, if we want to be lazy we can forget completely about the crazyness of of tensor calculus in Riemannian geometry and do everything with integral geometry instead. Nobody has ever made sense of the Gauss-Bonnet-Chern integrand in higher dimensions after all, so who cares? Well that was Gauss-Bonnet-Chern. Having trivialized that one, we can look at the curvature K which is a d-point correlation function of sectional curvatures. What happens now however is that due to the non-triviality of the frame bundle and because we need normal coordinates, we can not use a global probability space. We need to chop up the manifold and glue the parts together. Now comes a bit of multi-variable calculus in the form of Lagrange multipliers. It turns out that the indices of critical points at the boundary depend on the dual cone defined at the point. It is here that a bit of convex geometry comes in, a subject in which Werner Fenchel has worked, independently of Allendoerfer and Weil. The upshot is that gluing works in general only if the selfduality is satisfied and the probability space has some isotropy condition. Otherwise, the probability spaces in different chambers of the manifold can be completely independent. This is important also if one looks at the situation from the physics point of view. Causality considerations absolutely forbid even considering global differential forms. We have to cut up the manifold after all. The trick is to do it without killing the manifold!
From the continuum to the discrete
[Added May 27, 2020 and updated May 30, 2020] Here is an other way to get from the continuum to the discrete. We have started with a Riemannian manifold M, and realized it as a geometric realization of an abstract finite simplicial complex G, a finite set of non-empty sets which is closed under the operation of taking finite non-empty subsets. Let 
We have seen that if we take at a Riemannian manifold M, which is chopped up into a simplicial complex G and if we look at a Morse function f on M, then it defines an energy function h(x) on the simplicial complex, which is integer valued. What happens however is that if we take it as so, then we have h(x)=1, because every simplex in M is a contractible and topologically a ball of Euler characteristic 1. This is actually already quite exciting because attaching the energy value 1 to each simplex is a Bosonic analogue of the Fermionic (topological story) where we attach the value $latx \omega(x)=(-1)^{{\rm dim}(x)}$ which adds up to the total energy given by Euler characteristic. The case h(x)=1 is actually even more interesting because it leads to a very symmetric story of the counting matrix of a simplicial complex. The energy of a sub-complex A is defined as 
Now, one might wonder, how the more topological energy interpretation 
