Before the summer school start, I was wrapping up some research on positive curvature manifolds with symmetry, which was mostly actually just learning the ropes of this fascinating area. There is a bit of a write-up.[PDF]. [Update: June 29: Here [PDF] are a few more thoughts about the the relation between positive curvature manifolds and force carriers in physics. ArXiv version.]
And also a video:
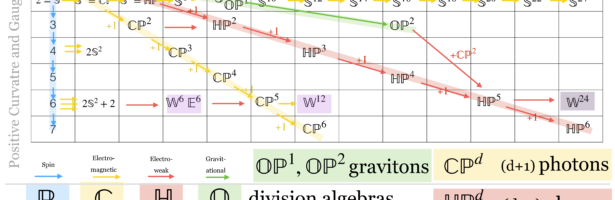
I was especially intrigued by the fixed point theory of symmetries acting on positive curvature manifolds. The fact that Euler characteristic is invariant allows dimension reductions. During the summer, I found that positive curvature manifolds with symmetry of dimension 8 or less have positive Euler characteristic. Checking with the experts revealed that the current record is 10. So, of course, I tried harder and hoped with a stronger structure theorem than Grove-Searle to get to dimension 12. That turned out to be wrong. Still, this work motivated me a bit to study the structure of the known positive curvature manifolds. I especially drew them in a grid in which dimension and Euler characteristic are the coordinates. Here is that periodic system of elements:
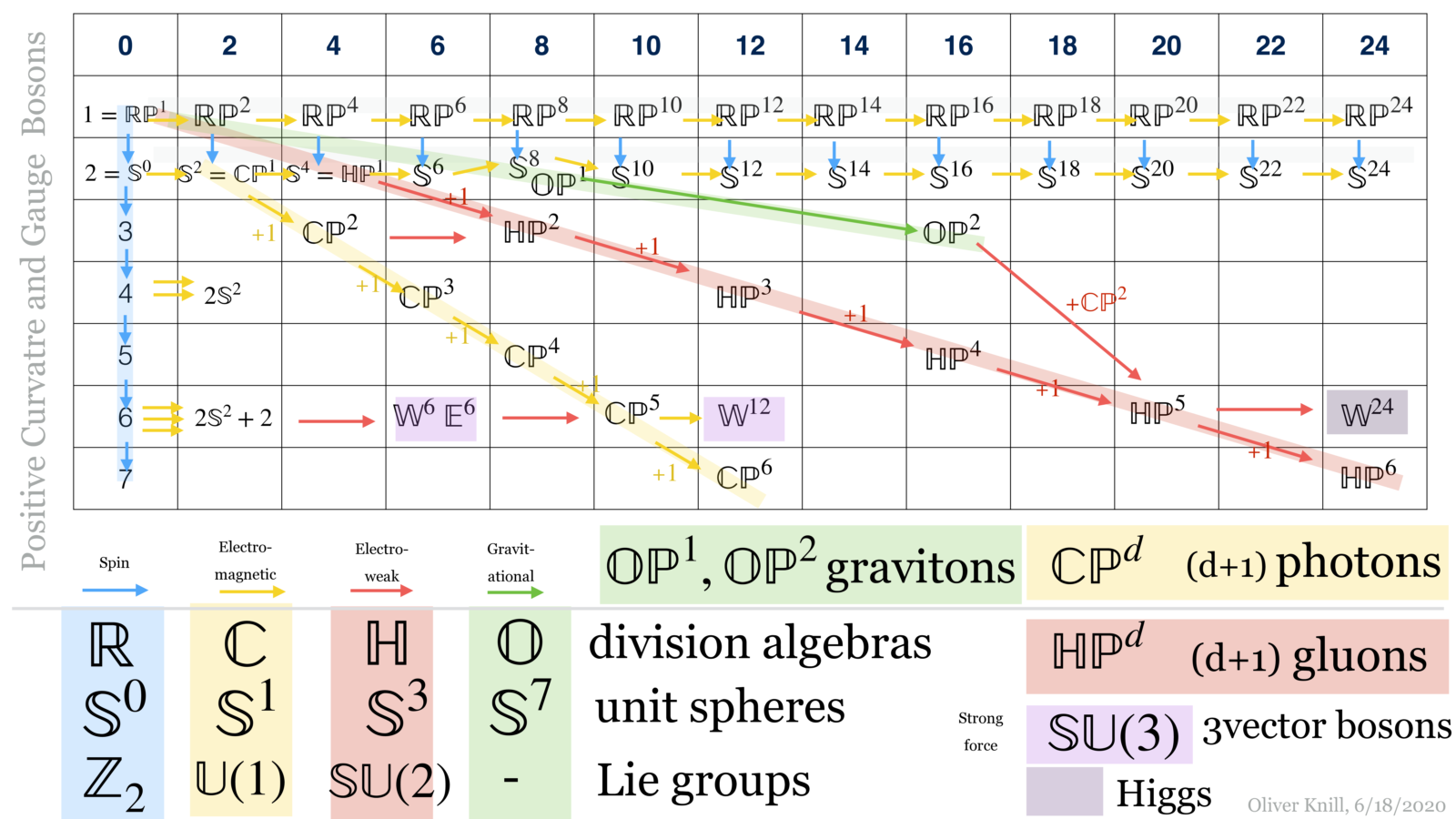
I also mixed in a curious affinity with physics. Relating fundamental forces with division algebras is an old idea but the relation with positive curvature manifolds appears to be new! There is a talk of the late Michael Atiyah still on youtube, where Octonions are mentioned in the context of gravity. The fact that there are only 4 normed division algebras makes the guess very natural. There is at first a bit of a mystery why the gauge group SU(3) appears. But in the positive curvature manifold story, they come up prominently and naturally in the form of flag manifolds (Wallach and Eschenburg manifolds). The octonions are very special, there is no associativity any more preventing further projective spaces beyond the Moufang-Cayley plane which is a 16 dimensional Riemannian manifold. Now, what happens with the Connor-Kobayashi theory is that one can revert it and construct from the fixed point set N the manifold M. The picture is that the possible extensions have to come from spheres which also are Lie groups. This produces restrictions. The octonion case is just special as its unit sphere is not a Lie group any more. But also gravity is special and of a different nature than the other forces. If you look at the video, you see the warning of Kepler who had the Harmonies Mundi picture of associating platonic solids with planets (which was completely invalidated once more planets were found) or Thompsons vortex knot picture of atoms which also did not pan out. More recently one has tried to bridge string theory with physics and it seems that it does not work. Still, in each case, the connection of a mathematical theory with physics motivates the mathematics, whether it is the study of regular or less regular polytopes, whether it is the study of knots or whether it is the study of super symmetry.
Why should there be a relation between positive curvature manifolds and physics? One can joke that Lie groups like to live somewhere, they need a home! They can of course live on linear spaces. One calls this representation theory. But linear spaces are boring places to live. Why not live on more interesting homes like compact manifolds? And if one takes compact manifolds, why not manifolds of positive curvature. One reason why positive curvature is appealing is that one has caustics. They do not exist in the negative curvature case. If a positive curvature manifolds allow for a symmetry, the caustic of any point always lives on the fixed point set which consists again of manifolds of positive curvature. So, there is, like in representation theory, a reduction theory possible. The interesting angle is that when looking at this reduction theory, the fundamental gauge groups appear naturally. If one takes this picture seriously, it makes it likely that the known list of positive curvature manifolds is actually already all there is (at least if one looks at the class of such manifolds with some symmetry).