From the Christmas Theorem to Particle Physics

The Christmas Theorem

Because Pierre de Fermat announced his two square theorem to Marin Mersenne in a letter of December 25, 1640 (today exactly 376 years ago) the theorem

is also called the Christmas theorem. The converse, the fact that a prime p of the form 4k+3 is not the sum of two squares can very easily be seen by looking at p=a²+b² modulo 4. The theorem is also called Fermat’s two square theorem. It turned out to be a bit older even, as it was found already in 1634 by Albert Girard (1595-1632).

Albert Girard	Pierre Fermat	Marin Mersenne

A proof from the Book

The best proof of the theorem is definitely the one of Don Zagier. It is a “proof from the book” in the sense of Erdös as this one-line proof can hardly be shortened any more:

On the discrete region with boundary x²+4yz=p, x ≥ 0, y ≥ 0, z ≥ 0 with integers x,y,z, there are two involutions T and S, where T(x,y,z) = (x,z,y) and S is given by S(x,y,z)=(x+2z,z,y-x-z) if x≤ y-z and S(x,y,z)=(2y-x,y,x-y+z) if y-x≤ x ≤ 2y and
S(x,y,z)=(x-2y,x-y+z,y) if 2y ≤ x. The map S has exactly one fixed point (1,1,k) if p=4k+1. Since the fixed points T and the number of fixed points of S are the same modulo 2, also T must have a fixed point of the form .

Sacret Mathematics?

The reference “proof from the book” has a non-secular origin as the agnostic Paul Erdoes once expressed that one should “believe in the book” and (with tongue in the cheek) accused God to “keep the most elegant mathematical proofs to himself”. Mathematics is a secular activity but it has historically often been driven and influenced by non-secular motivations. The Mesoamerican cultures, Sumerian cultures, the Pythagoreanism in Greece, Magic squares in China etc. The Hindu, Islamic, Buddist, Jewish and Christian religions have influenced mathematics considerably. The motivations were varied:

1. Calendars: Understanding the mathematics to develop calendars was an early motivation and calendars are important for rituals and celebrations.
2. Practical use: There were also political or practical reasons: the development of ciphers by Arabic and Christian mathematicians (Al-Kindi developing the first attack on poly-alphabetic ciphers, the monk Johann Trithemius creating an early version of the Vigenère cipher).
3. Meditative use: Then there is the meditative use of mathematics like the Mandalas in Hinu or Buddhist symbolism, duality in Yin and Yang, Arabic ornaments leading to classifications of tesselations or floor mosaics (the Kepler-Poinsot polyhedron in the St Marks Basilica for example).
4. Entertainment and art: Then there is entertainment value in modern “new age” Sacred geometry cults adoring objects like the flower of life or the Metatron cube.
5. Psychoanalytical value Many of these naive revelations are of artistic or even psychoanalytical value (C.G. Jung).
6. Historical insight: They are not without scientific significance because they have influenced and motivated scientists. They still do so today even so the influence is maybe primarily of historical nature when trying to understand the motivations of our ancestors.

Is Mathematics necessarily elegant?

Even the possibility of the existence of a divine can motivate to find elegant and beautiful structure even if there is no evidence that it might exist. The believe that nature is elegant is a motivator but could be wrong. History is full of examples: one once thought the planets move on circles or epicycles and this belief was shattered by Kepler. Kepler once thought that the planetary motion satisfy a “harmonices mundi” connection with Platonic solids and this was shattered by more evidence. One once thought that one could find a complete axiom system covering all mathematics and this was shattered by Goedel and Cohen; there was the believe that one could solve the quintic and this was shattered by Abel and Galois, one thought that one can justify Euclidean geometry and this was shattered by Gauss, Bolay and Lobachevski; one had once the impression that one can compute anything and this was shattered by Turing, one thought once that one can predict the future using a Laplace demon type device and this was shattered by chaos theory and quantum mechanics. One once thought that there is a simple proof of Fermat and this was destroyed by centuries of failures and by a proof which uses heavy machinery from algebraic geometry. So, naive gut feelings have often been wrong, but they had been inspiration or motivation. We don’t know for example whether the binary Goldbach or the Riemann conjecture hold true but we are driven by the believe that they have proofs we can access. Of course we have learned from history and many attempts have been made to find counter examples. Its like treasure hunting. We believe the treasure is there, but we don’t know. Fortunately, in the past, the failures of finding what has been believed turned out to be even more exciting than a the actual find. The modern theory of celestial mechanics is a thousand times more interesting than Kepler’s Harmonices mundi story which looks today rather infantile. There is chaos, there are collision singularities, there are non-collision singularities there are numerical schemes allowing us to land robots on Mars or photograph Pluto. Any of the above examples show that original naive religious believes about beauty have been vaporized by a firework of even more beautiful structures than anticipated. I personally have no doubt that this will also continue even so this is only a guts feeling. The physicist Lisa Randall once said that there is no mathematical theorem assuring that the laws of nature have to be elegant. While the possibility of a simple structure can drive us, it can be important to keep this in mind in order not to get disappointed. Also, what is “simple” or “elegant” or “beautiful” has changed over time. We believe now that the Newton laws of physics are simple as they are described by a universal n-body differential equation. However, this is not simple at all, as Poincaré has shown. There are simple open problems like the problem of almost everywhere existence of solutions to the n-body problem, which is one of the famous problems in a list of 15 given by Barry Simon. I myself spent a year on this problem and even thought at one point to have a proof using Vlasov dynamics. This turned out to be too naive and requires to look at a BBGKY hierarchy which leads to a technical mess. Even the Vlasov case in the case of potentials with singularity is difficult.

A poetic reinterpretation of the Christmas theorem

The Christmas theorem of Fermat has a poetic interpretation in terms of particle physics: it tells that rational primes of the form 4k+1 are Bosons consisting of an electron-positron pair and that primes of the form 4k+3 are Fermions consisting of neutrini. This leads to allegorical reformulations of quadratic reciprocity: if (p|q) is the Jacobi symbol then (p|q)=-(q|p) if both particles are Fermions. Otherwise, if one is a Boson, then (p|q) = (q|p). What does this mean? Lets explain it with example and take two Bosons 5 and 13. Now (5|13) = -1 because 5 does not appear as a square k² modulo 13 (the list of squares is (1, 4, 9, 3, 12, 10, 10, 12, 3, 9, 4, 1, 0). Also 13 is not a quadratic residue modulo 5 because 3 does not appear in the list (1,4,4,1,0) of squares modulo 5. So, also (13|5)=-1. But lets take two Fermions like 3 and 11. We have (3|11)=1 because 3=5² modulo 11 and (11|3)=-1 because 11 = 2 modulo 3 does not appear in the list of squares (1,1,0) modulo 3. We see that the Fermionic nature of the primes had the effect that switching the two particles changes the sign of the Jacobi symbol (3|11)=-(11|3). What is the value of this allegory? It allows us to remember the quadratic reciprocity theorem in an intuitive way. When I learned the theorem in a number theory course, I had first to memorize the formula by heart. Now, I don’t have to remember that formula any more. I know a story which guides to the theorem. The story still does not reveal why the theorem is true. For seeing this, one has to look at the proof: it uses ideas which are fundamental to physics like the structure of symmetry. The Eisenstein proof for example shows that (p|q) is a “charge operator” as it is (-1)^k where k is the number of lattice points below the diagonal in [0,p] x [0,q]. Now, (q|p) is the number of lattice points above the diagonal. As there are no elements on the diagonal and the sum of the lattice points is (p-1) (q-1)/4, the result (q|p) (p|q) = (-1)^(p-1)(q-1)/4 follows. Now we are happy because we have insight why the particle structure of the rational primes is true.

A Lepton allegory

In “particles and primes”, an allegory between Leptons and primes in the complex plane C as well as Hadrons and primes in the quaternion algebra H was developed. Since the complex and quaternion algebras C and H are the only associative, complete division algebras and already as Euclidean spaces are characterized as the ones for which the unit sphere is a continuous Lie group, these structures are remarkably unique among all categories in mathematics. What other structures given axiomatically by simple rules have the property that it leads to such a confined list of examples? In the complex plane, the rational primes of the form 4k+3 are no more prime in C. They decay into two primes a+ib and a-ib which according to “particles and primes” is an “electron-positron” pair. The remaining odd primes, which are of the form 4k+3 are the “neutrini”. The remaining primes in C have norm 2 and are of the form 1+i, 1-i. They are ramified in the sense that they are gauge equivalent under a unit in C. Like the neutrini, they are uncharged but they are special in many respect, especially in factorization and quadratic reciprocity laws. The neutrini primes are special in that for them, the square root of their norm is prime, not the norm N(a+ib) = a^2+b^2. One can remember this as neutrini are light. The neutrini are also Fermions in the sense that (z|w) = -(w|z) for two Fermions. The rational primes of the form 4k+1 which decay by the Christmas theorem into two Fermions behave as a Fermion pair like a Boson: the quadratic reciprocity tells (z|w)=(w|z) if one or both of the rational primes z,w are a Boson.

A hadron allegory

In order to get an analogue of Hadrons, I had proposed to look at two equivalence relations among primes in the quaternion algebra: a weak and a strong one. Two primes are weakly equivalent if there exists an element in the unit sphere SU(2) of H which maps one into the other. Two primes are strongly equivalent if there exists an element in U(3) (acting on three complex planes hinged together at the real neutrini line), which maps one into the other. It turns out that for odd quaternion primes (which are either Lipschitz or Hurwitz primes) the weak equivalence classes within each strong equivalence class are of two kind: they consist of either 2 or 3 elements. The case with 2 members is a Meson, while the case with 3 members a Baryon. The units in H are the vector Bosons, the units in C are the photos. The gluons are associated to the U(3) symmetry, related to the strong force. They are not individual particles like the photon or gauge Bosons and are confined to members of the equivalence classes which are the quarks. As in the complex case, the primes of norm 2 are Higgs like. The U(3) or SU(3) symmetry is a bit strange in that it acts in a nonlinear way but affects the three complex planes hinging together at the real line. Now this picture is also motivated from a physical observation, the phenomenon of neutrino oscillations. The neutrini, associated to primes in the real axes belong to any of the geometric evolutions defined on the three planes.

Quaternion valued quantum mechanics

“Particles and primes” also suggests to look at quaternion-valued quantum mechanics. First of all, classical quantum mechanics emerges naturally in any geometry as a Noether symmetry: just let the system go in its isospectral set. Even if we start with a real exterior derivative, the deformed derivatives still enjoys the same cohomology. The deformation leaves the Laplacian invariant. But under the hood, a lot of fairy dust is spread out: space expands. The Dirac operator develops a diagonal part which means “dark matter” not visible by the usual quantum mechanics. Space expands inflationary: there is an initial bump. This is not swooped in like in classical cosmology, but it is a mathematical result, which holds universally for any geometry with an exterior derivative. Especially for Riemannian manifolds or graphs. Now, every of the three basic complex planes in H has such an isospectral deformations going on (deforming three commuting exterior derivatives). There is no reason why the time scales in these three planes should be different (throw three rocks into space and they will rotate differently in general). Now, the H-valued evolution features under the hood automatically three different time scales. These are the three particle flavors we see. The three exterior derivative evolutions come together on the real line, where they hinge together. The particles which live there now can fluctuate. These are the neutrini oscillations which are observed.

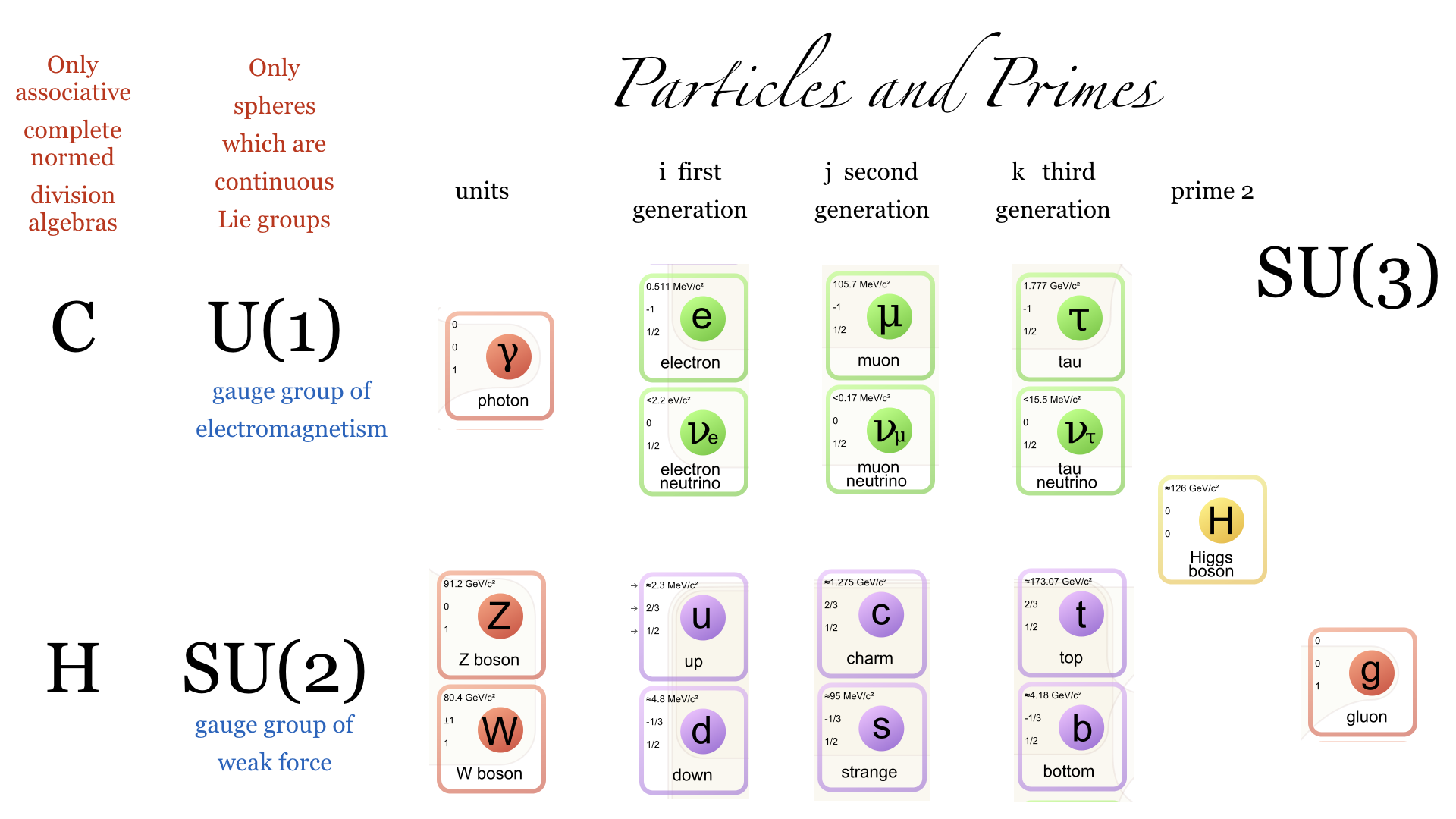Particles and Primes, Comparing the structure of the standard model of particle physics with the structure of the primes in the associative, complete, normed division algebras. The graphic uses blocks of entries in this graphics.

Magic and caution

Its Christmas day, so why not look at some magic? Especially after having drunk some champagne, one is allowed to be a bit exuberant:

• Hurwitz-Frobenius gives the structure of the fundamental forces.
• The Standard model is natural.
• Inflation and expansion of space is a universal feature of symmetry
• Dark matter develops in any geometry through isospectral deformation.
• Neutrini oscillation appear naturally as neutrini appear in all three isospectral deformations.
• Only three particle flavors exist.
• There is no GUT. C and H are special as their unit spheres are the only spheres which are Lie groups.

It is important to remember however that this is just a Christmas story which most likely has little to do with reality. Indeed, it is today often forgotten that:

But even if there should be no match with particle phenomena observed, the just outlined structures lead to natural geometric pursuits and questions. Indeed, many combinatorial questions remain open in the above topics. Whether there are will be applications in physics, remains to be seen.