The unimodularity theorem proof

[Update: January 19, 2018]. Sajal Mukherjee and Sudip Bera from the Visva Bharati University in Bolpur found a new simple proof
of the theorem and sent me a preprint. Their article might appear later, they
have agreed that I mention it here: it is the analysis what happens when one adds a new vertex.
This enlarges the matrix not only by one row and column. But one can analyze the situation
by looking at the partitioned matrix, do some column operations, then do some row operations
and then use induction. I myself had tried to analyze the new permutations obtained when
adding the new rows and columns. ]

The unimodularity theorem

The proof of the unimodularity theorem is written down and submitted to the ArXiv. As it will take a few days until the preprint appears there, here is a local version. The result is now formulated more generally for discrete CW complexes. The most natural set-up however is probably the case of an abstract finite simplicial complex. The connection graph of such a geometry is the finite simple graph where the vertices are the simplices=faces and where two are connected, if they intersect. We prove that if A is the adjacency matrix of such a connection graph, then 1+A is unimodular. Actually, the determinant is the product of the $\prod_x (-1)^{dim(x)}$ over all simplices in the complex. [Compare that with the Euler characteristic which is $\sum_x (-1)^{dim(x)}$ ]. We call the Fredholm determinant the Fredholm characteristic and the product the Fermi characteristic of the geometry.

The proof idea

The proof took more than 9 months to be found but is now quite clear: the key is a multiplicative analogue of the Poincaré-Hopf theorem telling what happens if a cell is added to the complex: we just multiply with the Poincaré-Hopf index which is $1-\chi(S(x))$ , where S(x) is the the unit sphere of the new cell, the boundary of the cell which got attached. Now since spheres always have Euler characteristic 0 or 2 and 2 happens for even dimensional spheres (corresponding to odd dimensional cells), it immediately follows that the Fredholm characteristic is 1 if there is an even number of “Fermion simplices” and -1 if there is an odd number of them. The unimodularity theorem opens a Pandora box of open questions. One of them is to gauge the significance of the Green function: what is the set of matrix entries of the inverse of 1+A? As we measure that it is invariant under Barycentric refinements, there might be more to it and it could be of topological interest. In any way, the result is what one can call a “nice theorem”: a theorem which equates two seemingly unrelated numerical quantitites:

Fredholm characteristic = Fermi characteristic

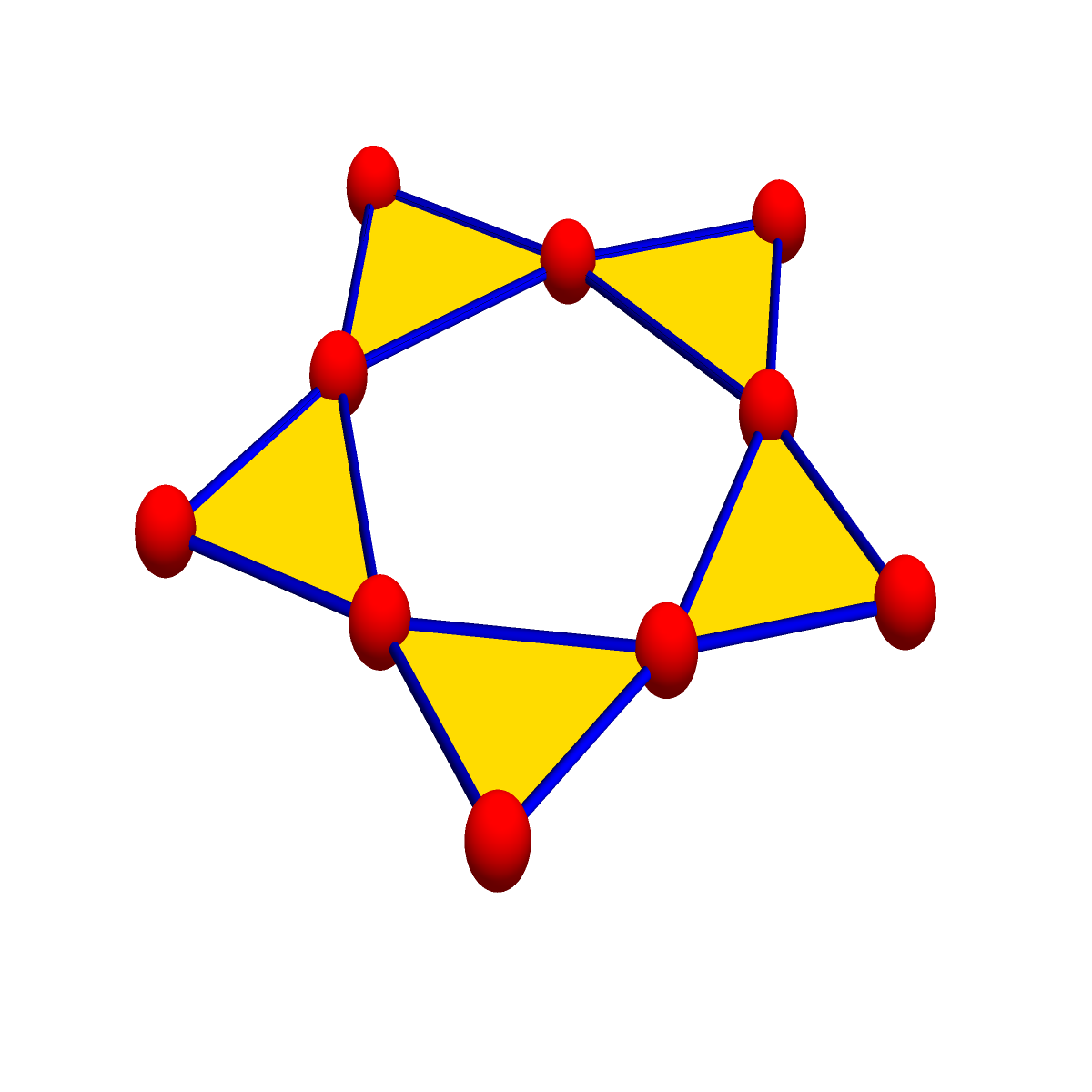
An illustration

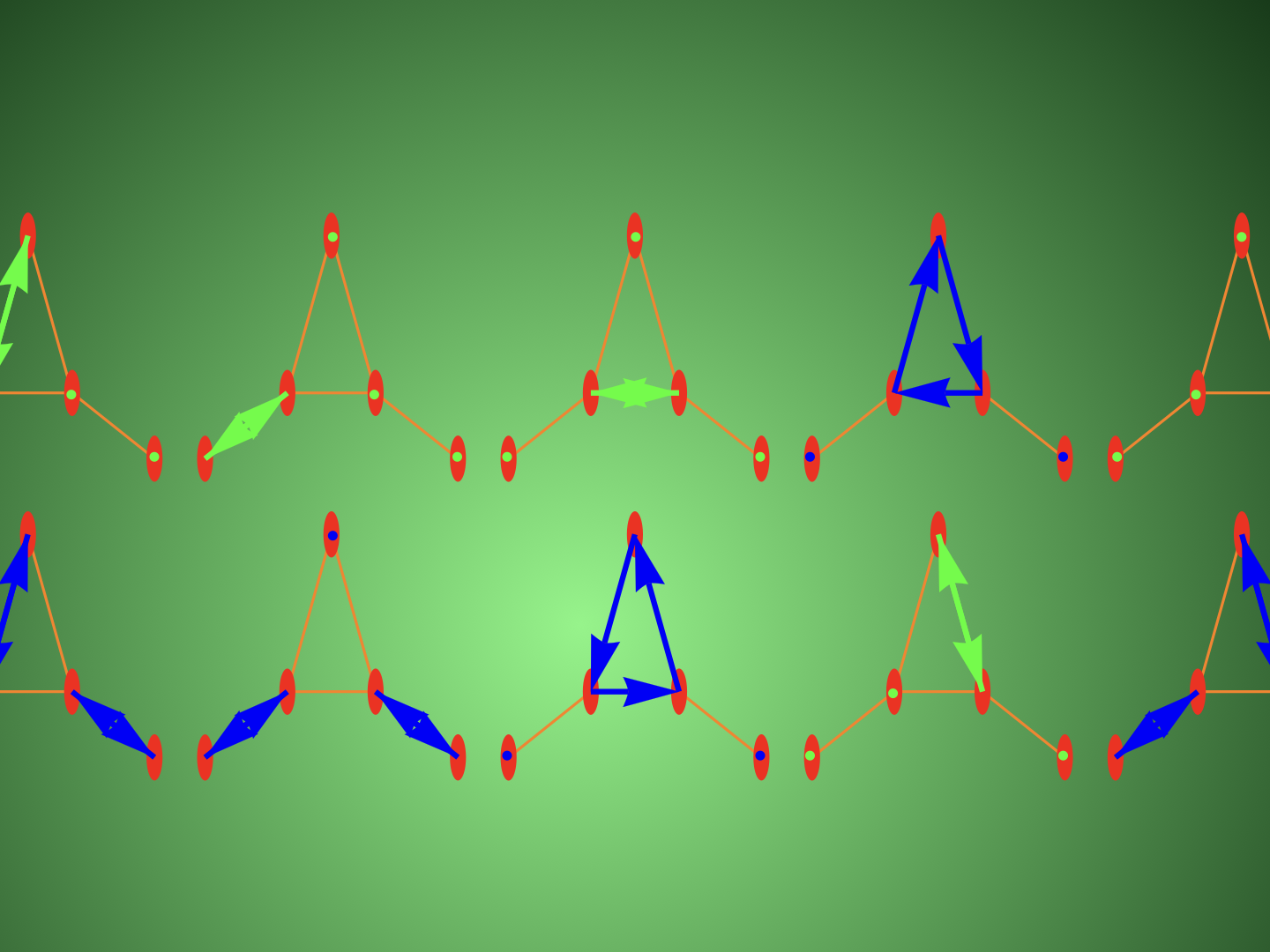
Here is again an illustration. The simplicial complex is the Whitney complex of the cycle graph C₅. As it has 5 odd dimensional faces so that the Fermi characteristic is $(-1)^5=-1$ . There are 318 even permutations and 319 odd permutations in the Leibniz sum of the Fredholm determinant which is 318-319=-1. Again, this might not look impressive but having the odd and even dimensional cases so close together is remarkable. Its not true at all for general graphs, this only holds for connection graphs of CW complexes. As the summands of the Fredholm determinant correspond to one dimensional directed paths, we can draw all possible paths. We see that Fredholm determinants are in some sense much more natural than determinants. For determinants, we only look at cyclic paths in the Leibniz sum. The additional identity matrix added allows the path to consist of “several one dimensional loops”. There can also be vertices which stay fixed or then loops of length 2 which are traditionally not counted as closed paths in graph theory. If one thinks as an undirected edge however as a collection of two directed paths, then this is also a closed loop even so the same edge is traversed twice. In some sense, the Fredholm determinant generates all one-dimensional oriented closed sub-manifolds of the geometry. A string theorist might look at it as the path integral over all possible one dimensional string configurations which are possible in the geometry. The picture left out the vacuum so that it fits better. There are two closed loops of length 10. Can you spot them? There are also two configurations featuring 5 loops of length 2. There is no room yet for 3 loops of length 3 evenso there are 10 vertices in the graph.

The Fredholm matrix 1+A for the connection graph is

$1+A=\left[\begin{array}{cccccccccc}1&0&0&0&0&1&1&0&0&0\\ 0&1&0&0&0&1&0&1&0&0\\ 0&0&1&0&0&0&0&1&1&0\\0&0&0&1&0&0&0&0&1&1\\ 0&0&0&0&1&0&1&0&0&1\\ 1&1&0&0&0&1&1&1&0&0\\1&0&0&0&1&1&1&0&0&1\\ 0&1&1&0&0&1&0&1&1&0\\ 0&0&1&1&0&0&0&1&1&1\\ 0&0&0&1&1&0&1&0&1&1 \end{array}\right]$ .

Its determinant is the Fredholm characteristic. It is -1. And here is a picture of the connection graph:

The unimodularity theorem

The proof idea

An illustration

Author: oliverknill