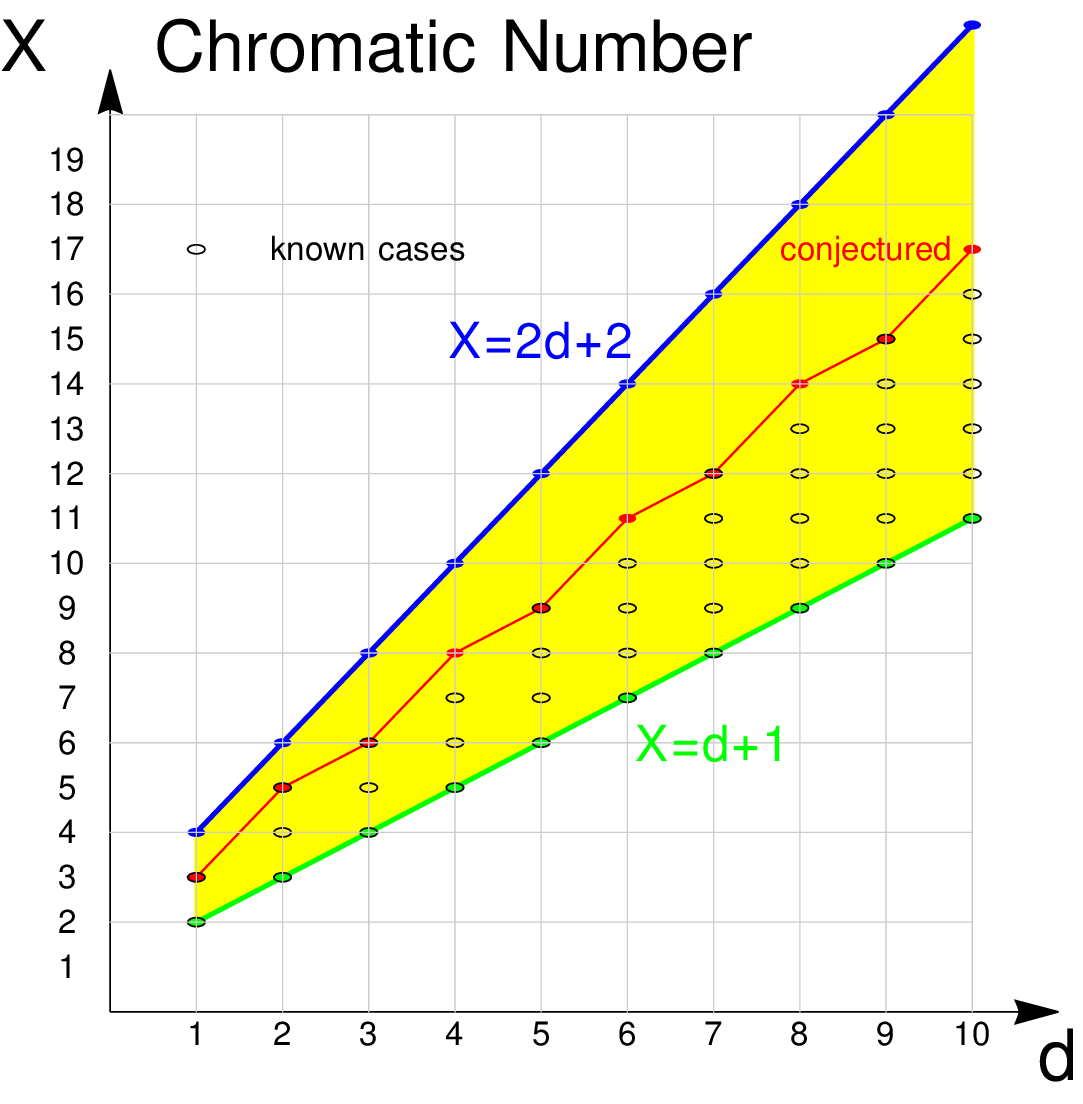
It is now 7 years, since I started to think about coloring discrete manifolds, graphs for which unit spheres are (d-1)-spheres, where d-spheres are d-manifolds which after a removal of a vertex become contractible. The problem has not gained any attention which is a good thing because there are many extremely low hanging fruits to pick here. Here are two ones which I had missed over all these years. The first one is a general bound X on the chromatic number of d-manifolds:
Theorem: for every d-manifold G.
Proof: Let G’ be the dual graph of G. This is the graph in which the vertices are the maximal d-dimensional simplices and two are connected if they intersect in a d-1 dimensional simplex. We show now that we can cover this graph by two different forests, where each tree generates itself within the graph. The simplices with the first tree will be colored by the first batch of (d+1) colors, the simplices of the second tree will be colored with the second batch of d+1 colors. We use that any collection of simplices in the dual graph which are a tree can be colored in a consistent way simply by “unfolding” the colors. Assuming the existence of the two forests which are embedded, we get a coloring with (2d+2) colors. How do we get the forests: start with a point and build the maximal tree which contains this point and is embedded in G. It is important that we insist on having the tree embedded and not that there are two points in the tree connected by an edge in G. All vertices in this tree are labeled to have distance 0 from the initial point x. Now Look at all end points of the tree and make them seeds of trees of the second part, again continuing each until they are maximal and still embedded and not covering anything already covered by the first forest. We call these vertices to have distance 1 from x. Continue like this until the entire graph G is covered. This procedure produces the forests.
The second fact is the construction of spheres of relatively large chromatic numbers
Theorem There are 3 spheres of chromatic number 6, and more generally 2k-1 spheres G with X(G)=3k and (2k)- spheres with X(G)=3k+1.
The chromatic number is an additive functional with respect to the join addition. Now C(5) + C(5) + … + C(5) is a 2k-1 sphere of chromatic number 3k.
Here is a presentation recorded last Saturday. It was prompted by two simple observations which pushed a bit my understanding of coloring manifolds. The movie has been re-uploaded as there had been technical difficulties with processing the movie (stuck for 3 days). Update June 5th. The original version with better 4K resolution finally made it. It is better as the board letters are really small.
Here is a slide presentations from 2014