A 2-manifold with boundary is a finite simple graph for which every unit sphere is a circular graph with 4 or more nodes or a path graph with 3 more nodes. The boundary is the set of vertices for which the unit sphere is a path graph, the interior is the set of vertices for which the unit sphere is a circular graph. The classification of 2-manifolds without boundary into topological types is the same than in the continuum. It is determined by cohomology and in particular by the Betti vector . The
gives the number of connected components. The
determines the genus. And
determines for connected manifolds about orientability. The list of Betti vectors for each connected component determines the type of the surface. For surfaces with boundary we also can reduce the classification to connected surfaces first. Then the Betti vector of the surface as well as of the boundary determines everything: since the boundary is a 1-manifold and so a finite collection of circles, we know the number of holes. Each of these holes now can be filled with either a disk or a Moebius strip to get a manifold without boundary. In the end, it only matters whether we have an even or odd number of Moebius strip glued in and that can be read of from
. The upshot is that the classification of 2-manifold graphs with or without boundary is the same than then 19th century classification for classical manifolds. There is no information at all lost in two dimensions by looking at finite mathematical models. This changes in higher dimensions, where in the classical setup, one has to distinguish PL, smooth or topological manifolds. The topology of PL manifolds is equivalent to the combinatorial frame work, where a d-manifold as a graph for which every unit sphere is a (d-1) sphere, and were we define a d-sphere as a d-manifold which when punctured becomes contractible and where a graph is considered contractible if there exists a vertex such that both S(v) and G-v are contractible. These inductive definitions are constructive and suitable for a finitist as Euclidean space is not involved.
| Type of curvature | 2-Manifold without boundary | 2-manifold with boundary |
| vertex curvature | 1-d(a)/6 | 2/3-d(v)/6 |
| edge curvature | 1/d(a)+1/d(b)-1/3 | 1/d(a)+1/d(b)-2/3 |
| face curvature | 1/d(a)+1/d(b)+1/d(c)-1/2 | 1/d(a)+1/d(b)+1/d(c)-2/3 |
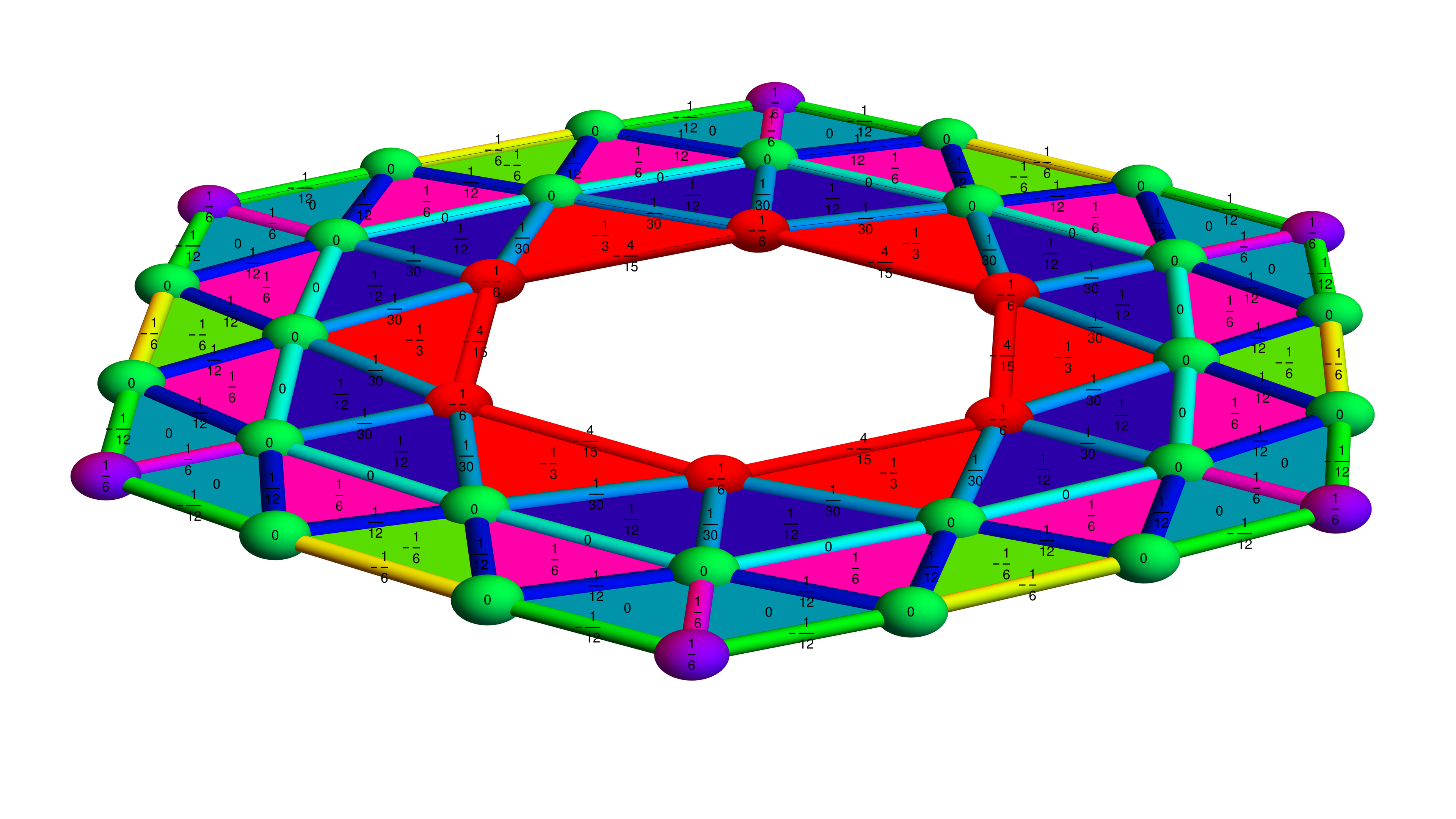
So, while very classical, the differential geometry of 2-manifolds with boundary can lead to new developments. We will look here at something which I’m not aware having been seen already. We first of all give formulas for the edge and face curvatures for 2-manifolds with boundary. We also give a Puiseux type formula for curvature which appears to be new. I started to look at the differential geometry of flat regions in 2009 “A discrete Gauss-Bonnet type theorem”. I got into the topic by accident and still find it fascinating. The starting point is that in the continuum, we have a nice intrinsic formula for curvature found by Pusieux which only involves the lengths or the spheres of radius
and radius
. The formula shows that for surfaces of positive curvature, the arc length of spheres tends to decrease while for surfaces of positive curvature the length of spheres increases more than in the flat case. The prototype is to look at circles near a maximum and circles near a saddle. The Puiseux formula is nice because by definition, this curvature is intrinsic. There is no need for a Theorema Egregium. I felt in 2009 that a Puiseux type formula might be a good curvature notion in the continuum. But in order to show that it is a good formula, we need to prove Gauss-Bonnet! I looked at the formula
in the discrete but could not prove a general Gauss-Bonnet formula with that. Indeed, Gauss-Bonnet in general fails. In my 2009 paper (appeared in 2010), I look at an even more specific case, where the manifold with boundary is part of the flat Euclidean (Hexagonal in the discrete) plane. One has to give quite precise definitions of region types so that the formula works. I also found in that paper that the curvature
in the interior and
on the boundary gives a curvature that works for any two dimensional graph with boundary. The sum of all these curvatures is always equal to 6 times the Euler characteristic of the surface with or without boundary. I then saw in the “Princeton Companion” that these curvatures are known. Later, when looking at graph colorings, the history of these curvatures appears to point as Victor Eberhard having it considered first in the 19th century. I in 2010 looked more into higher dimensions, climbing up dimensions 3,4,5 etc until finding the general formula for curvature in “A graph theoretical Gauss-Bonnet-Chern Theorem” (from 2011). This formula
involves the f-vector of the unit sphere
. A few years later I found that the formula had been known by Norm Levitt already in 1992. I still think that my 2011 paper is interesting as it looks at the manifold cases and discovers for example that the curvatures are constant zero for odd dimensional manifolds (something I could not prove yet then). Index expectation (2012) then did the job and explains why curvature for odd dimensional manifolds is constant zero. Index expectation brings in integral geometry and provides also a natural link from the discrete to the continuum. The reason is that we both have in the discrete and continuum nice Poincare-Hopf theorems and that we can place a discrete space into a higher dimensional space and look at functions induced by linear functions in the ambient space. Both in the discrete as well as in the continuum, one has for almost all directions an induced Morse function on the geometry and that the expectation is a known curvature. It is the Gauss-Bonnet-Chern integrand in the continuum and it is the Levitt curvature in the discrete. That the Levitt curvature is natural can be seen from the fact that it generalizes to a Gauss-Bonnet formula for the generating function
. One has now
. See “Dehn-Sommerville from Gauss-Bonnet” (2019). I used that even in a single variable calculus course! Note that this formula is very general and holds for any graph. It also gives a nice small recursive way to compute the f vectors. I even submitted the following one -line program to a WTC2023 competition. In any way, it shows how natural this curvature is.
f[s_,x_]:=Module[{v=VertexList[s]},n=Length[v];1+Integrate[Sum[w=v[[k]];f[VertexDelete[NeighborhoodGraph[s,w],w],t],{k,n}],{t,0,x}]];As mentioned in the talk, the edge and face curvatures can provide second order curvatures of Puiseux type. What we can do for example is to distribute the edge curvatures obtained to the vertices again By pushing all edge curvatures to both vertices equally, we get then for manifolds without boundary .