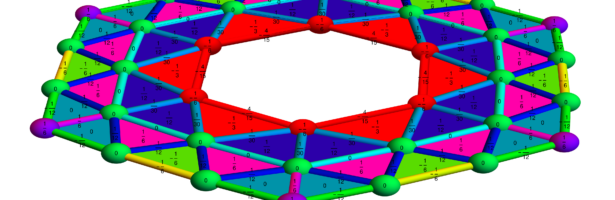
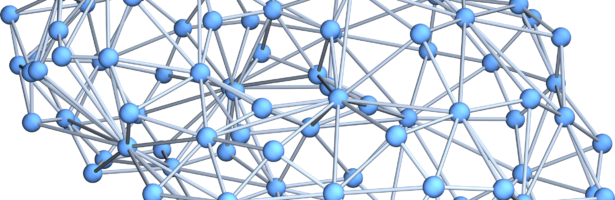
Geodesic Code Cleanup
[Update March 23: a paper draft is up. The ArXiv version contains also more code.] Spring break is a good time for some programming and cleanup. I reorganized our home office, took everything apart and rewired the half a dozen computers new, got rid of about 30 old harddrives, mostly …