A Dirac matrix D =d+d* above is deformed with the QR decomposition of exp(D)=QR to Q*DQ. The Diagonal part is the dark matter stuff. The geometry is a random graph with 15 nodes and 80 edges. It produced a 6 dimensional simplicial complex (Whitney complex). The dark matter lemma assures that we still have a Dirac matrix. But now D’=d’+d’*+m has a dark matter diagonal part in general.
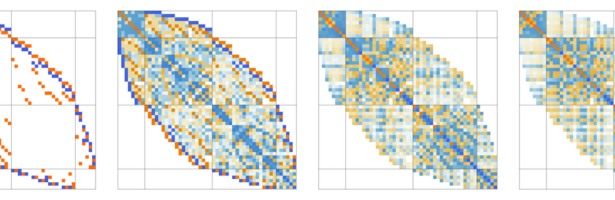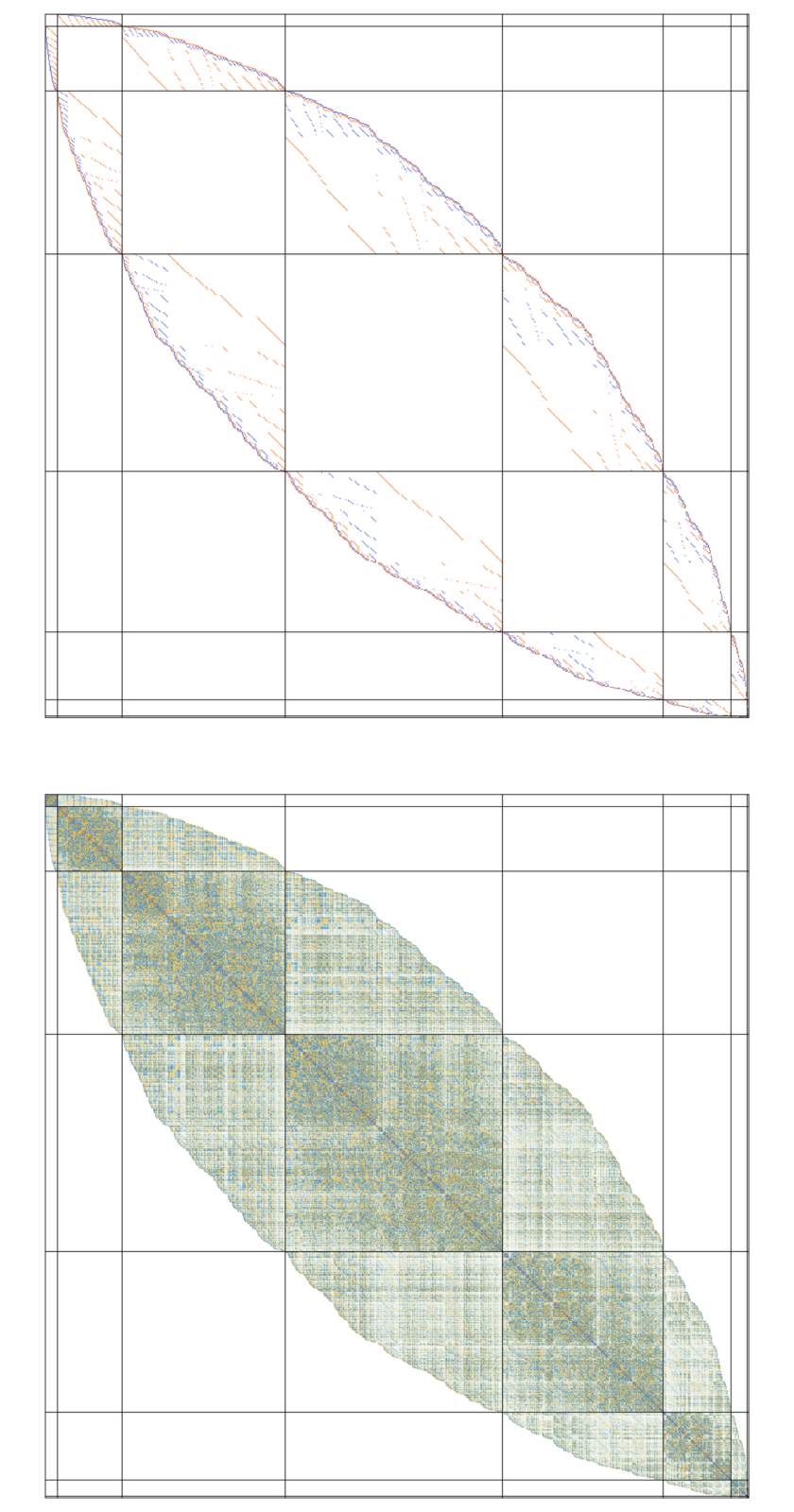
A real symmetric matrix is called a Dirac matrix, if it is a block Jacobi matrix in which the side diagonal entries are nilpotent, meaning . For such a matrix, the square is called the Laplacian. It is block diagonal . If is a continuous function such that is invertible, we can form the QR decomposition of f(D)=QR and a new matrix . Given a Dirac matrix, let be called its Betti numbers, where is the geometric Laplacian. Here is a lemma from linear algebra. In a geometric setting, d is an exterior derivative appearing for example in the Maxwell equations for a given charge-density current j, where the dark matter term m is missing. The name “dark matter” is natural because in cosmology, measurements of galactic motion suggest (Zwicky 1933) that there is matter and energy that is not interacting electro-magnetic but manifests gravitational. The lemma below is pure linear algebra; one is certainly allowed to speculate however that the nature of dark matter is purely geometric: if we let a geometric object move in its symmetry group, the result shows that non-electromagnetic terms m will develop. The diagonal part in general grows while the off diagonal part shrinks. If derivatives d shrink, Connes distance formula implies that space expands. In 2013, we already looked at continuous time deformations of a Dirac matrix. The differential equation were Lax Pairs D’=[B,D], where B=d-d^* in the simplest case. See the June 1, 2013 and June 24, 2013 paper. As pointed out there, one can ask “why this deformation happens?” The answer is that no deformation has probability zero in the symmetry group which is a continuum even if space is a finite set. To repeat a picture from my 2013 paper: If you release a stone in space it will in general move and rotate relative to your fixed coordinate system because the probability of having zero momentum and zero angular momentum is zero. The isospectral symmetry also appears in the continuum like in Riemannian geometry where the smallest blocks of d are called “gradient” and “curl” but the operators deform as pseudo differential operators. Mathematically, the deformation defines a cochain homotopy of the geometry because the cohomologies do not change. The underlying space, like a manifold or a simplicial complex, does not change. But since the measuring stick d changes, distances change by Connes formula: if you would decide to shrink the gradient by a factor 2, then all direcdtional derivatives would shrink by a factor 2, which is equivalent that space is expanded by a factor 2. For the continuum integrable Lax deformations, I showed in 2013 that the expansion rate is inflationary. There is a rapid first expansion which then slows down. The intuition is that in a nonlinear setting, not only m,d but md are a driving forc for the expansion but since this driving force becomes smaller over time, the expansion rate will slow down too. Mathematica code illustrating this can be found for example here from November 19, 2020 . I don’t know why I never looked at the QR (discrete time isospectral deformations) until 2 weeks ago in a coffee shop in Medford. It is surprising because analog problems (both Lax and QR) in random operator settings appear in my thesis (part 1 and part 2 and part 3). That work was primarily about Dirac stuff in one dimension (facoring a Jacobi matrix and random Jacobi matrix as a square of an other Jacobi matrix over a doubled system). I had also looked whether it is possible to isospectrally deform the Laplacian in higher dimensions. There is a classical “no go” theorem showing that this is not possible. In the “on three levels” paper from 1994, a paper written in Les Diablerets, while my wife Ruth was in a conference there (I could have fun climbing, running and skiing in that beautiful area while the conference participants had to listen to lectures!). The upshot that deformations are possible if one can factor. The obstacle is that when doing a factorization, a “dark matter part” m has to be added to the “matter part” d in general. In the continuum this manifests that we have to factor in a space of pseudo differential operators and that the deformation does not produce a Riemannian metric in general (it is known that deformations of a Riemannian metric are in general is not possible preserving the spectrum of the Laplacian).
In any case, here is the lemma:
Dark Matter Lemma: D’ is again a Dirac matrix. Its Betti numbers are the same than the Betti numbers of D.
Dark matter has been suggested by Zwicky in 1933 and 1936 based on observations. Fritz Zwicky was mentioned during the presentation. He is an anti-hero in science because he was kind of a not-so-polite fellow, especially with his fellow scientists (to be more clear: he was considered an arrogant prick. One can still see this today. Very few know about Zwicky). He was an independent thinker however and so a hero of mine (my biography entry in an encyclopedia, a lecture on creativity in math 22b 2022 and an essay and bio from 1998 to the 100th birthday of Zwicky. It started with an essay to a competition, which uses amodified an idea of Zwicky for space travel. Zwicky had suggested to move the entire solar system to a new destination. This could be accomplished by modifying the sun burn. The asymmetric burn and so develops some thrust and moves the entire solar system with it. My essay was mentioned in this maco-engineering book.
As for the proof sketched in the talk: the idea is to define a matrix algebra defined by D, which has the property that if one makes a QR decomposition in it, then Q remains in that algebra. I have still to write this down.
But the idea hatched while proctoring the final exam in math S 21a (see the exam [PDF], I’m especially proud about the TF problem: “any function that simultaneously satisfies the Laplace and wave equation must be linear” because any AI asked so far gives the wrong answer. The Laplace and wave equation of course also appear in the finite and . The sign is because has negative eigenvalues and so is identified with -L. The two equations imply and . In the calculus case, this means from which one can easily get seduced to conclude that u must be linear. But any u = t v with harmonic v works. One can take in the continuum u(t,x) = tx. It satisfied the Laplace and wave equation but is not linear. I gave full credit for that TF problem anyway because I myself got it wrong when writing the problem and because one could interpret “linear” as multi-linear, linear in each of the variables.
