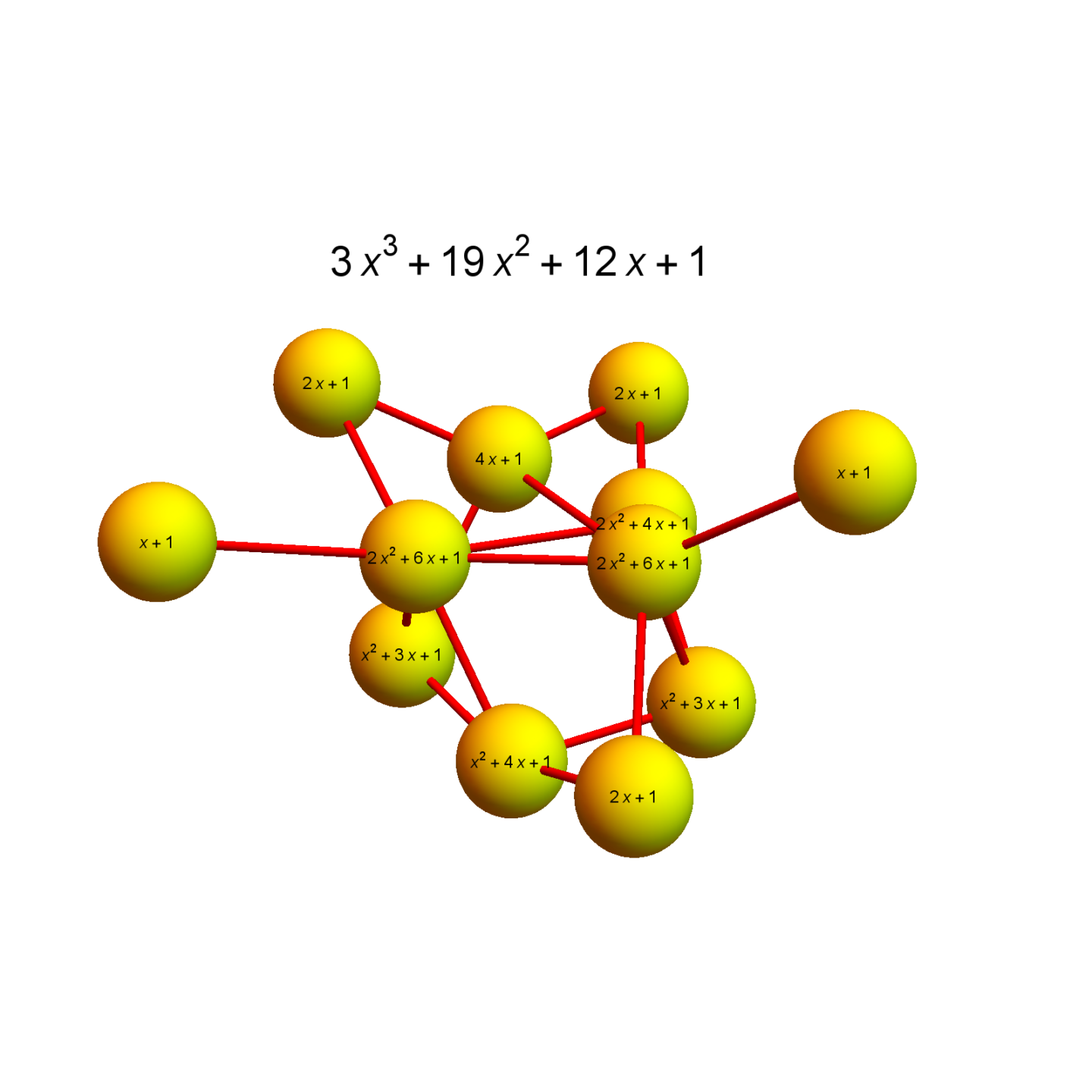
Gauss-Bonnet for the f-function

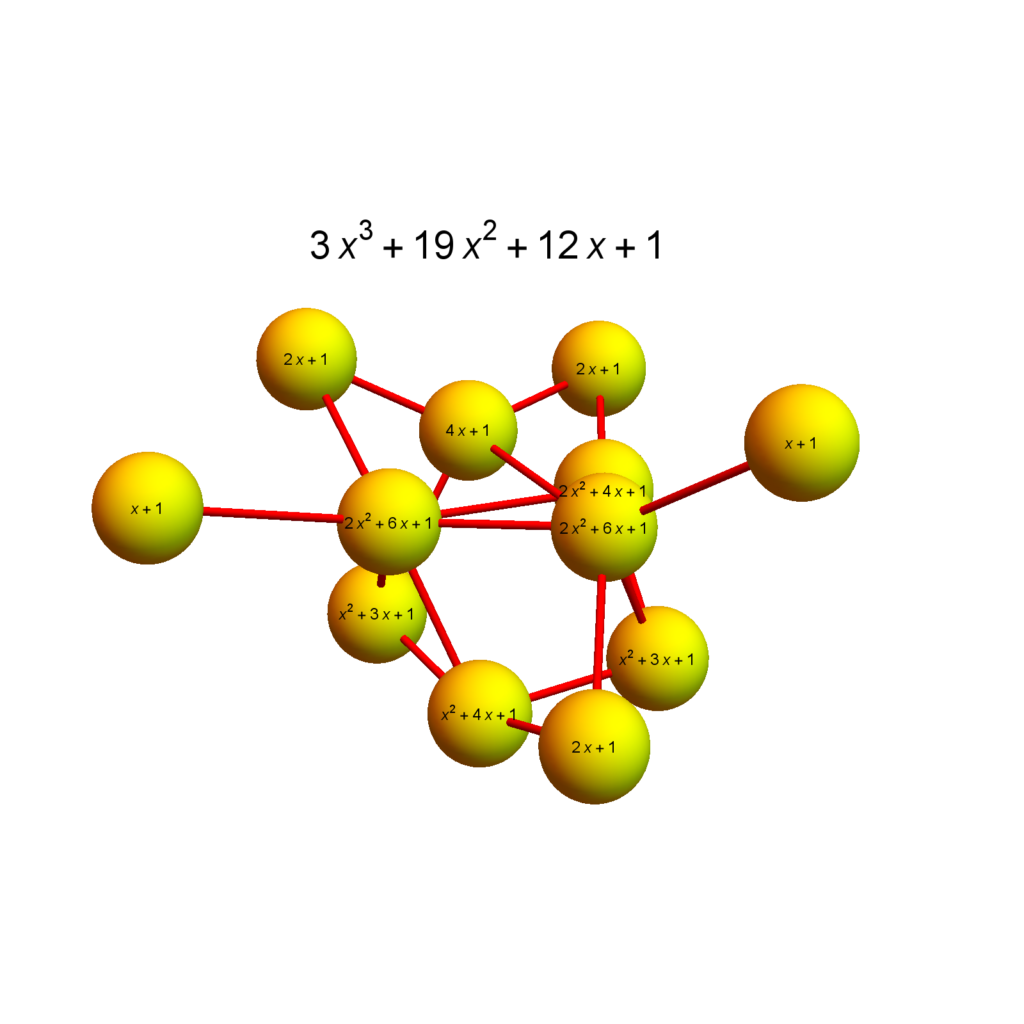
Let G=(V,E) be a finite graph. The f-function $f_G(t)=1+f_0 t + â€¦ + f_d t^{d+1}$ encodes the number $f_k$ of complete subgraphs $K_{k+1}$ of $G$. Let $F_G(t)=\int_0^t f_G(s) ds$ be the anti-derivative of $f_G$. For a vertex $x \in V$, then unit sphere $S(x)$ is the graph generated by the vertices directly attached to $x$. The curvature function at a vertex $x$ is $K_x(t) = F_{S(x)}(t)$.

Theorem: $f_G(t) = 1+\sum_{x \in V(G)} F_{S(x)}(t)$.

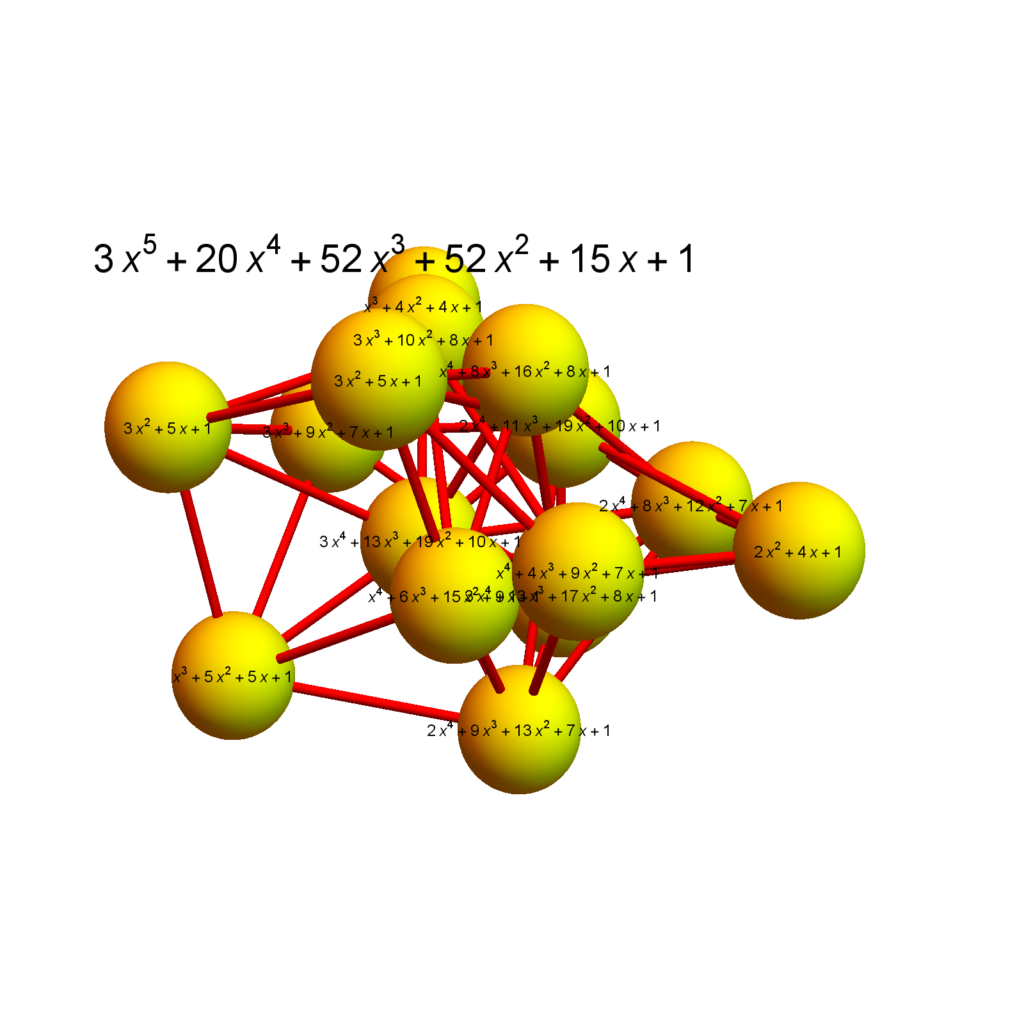Gauss Bonnet for the f-function. The sum of the curvature functions is the f-function.

An other example with maximal dimension 4. Evaluated at x=-1, we get the Euler characteristic

In analogy to the “Theorema Egregium”, this theorem should be called the “Scrumtrilescent Theorem” …..

The following lines of code were attached to the paper: (a bit updated in http://www.math.harvard.edu/~knill/graphgeometry/papers/zeros.pdf).

[Blog update of May 28, 2019, there had been problems with < and > symbols in the Mathematica codeÂ as these signs are interpreted differently in HTML by WordPress. It is now corrected and should work with copy paste.Â WordPress has become more confusing with classic word press editors, new block editors and code editors and then HTML. Each handles things differently. The only thing which actually worked was by editing the HTML.]

By the way, there was a demonstraction project on Gauss-Bonnet already here from 2012 (Dimension and Euler characteristic) and here (Gauss-Bonnet and Poincare Hopf), which both dealt with the theorem where the curvatures were scalars, not functions. Of course, also Poincare-Hopf holds in the function case. We will make use of this elsewhere:

UnitSphere[s_,a_]:=Module[{b=NeighborhoodGraph[s,a]},
  If[Length[VertexList[b]] < 2,Graph[{}],VertexDelete[b,a]]];
UnitSpheres[s_]:=Module[{v=VertexList[s]},
  Table[UnitSphere[s,v[[k]]],{k,Length[v]}]];
ErdoesRenyi[M_,p_]:=Module[{q,e,a},V=Range[M];
  e=EdgeRules[CompleteGraph[M]]; q={};
  Do[If[Random[] < p,q=Append[q,e[[j]]]],{j,Length[e]}];
  UndirectedGraph[Graph[V,q]]];
CliqueNumber[s_]:=Length[First[FindClique[s]]];
ListCliques[s_,k_]:=Module[{n,t,m,u,r,V,W,U,l={},L},L=Length;
  VL=VertexList;EL=EdgeList;V=VL[s];W=EL[s]; m=L[W]; n=L[V];
  r=Subsets[V,{k,k}];U=Table[{W[[j,1]],W[[j,2]]},{j,L[W]}];
  If[k==1,l=V,If[k==2,l=U,Do[t=Subgraph[s,r[[j]]];
  If[L[EL[t]]==k(k-1)/2,l=Append[l,VL[t]]],{j,L[r]}]]];l];
Whitney[s_]:=Module[{F,a,u,v,d,V,LC,L=Length},V=VertexList[s];
  d=If[L[V]==0,-1,CliqueNumber[s]];LC=ListCliques;
  If[d>=0,a[x_]:=Table[{x[[k]]},{k,L[x]}];
  F[t_,l_]:=If[l==1,a[LC[t,1]],If[l==0,{},LC[t,l]]];
  u=Delete[Union[Table[F[s,l],{l,0,d}]],1]; v={};
  Do[Do[v=Append[v,u[[m,l]]],{l,L[u[[m]]]}],{m,L[u]}],v={}];v];
Fvector[s_]:=Delete[BinCounts[Map[Length,Whitney[s]]],1];
Ffunction[s_,x_]:=Module[{f=Fvector[s],n},n=Length[f];
  If[Length[VertexList[s]]==0,1,1+Sum[f[[k]]*x^k,{k,n}]]];
DehnSommerville[s_]:=Module[{f},Clear[x];f=Ffunction[s,x];
   Simplify[f] === Simplify[(f /. x->-1-x)]];
Curvature[s_,x_]:=Module[{g=Ffunction[s,y]},
  Integrate[g,{y,0,x}]];
EulerChi[s_]:=Module[{f=Fvector[s]},
  -Sum[f[[k]](-1)^k,{k,Length[f]}]]
Curvatures[s_,x_]:=Module[{S=UnitSpheres[s]},
   Table[Curvature[S[[k]],x],{k,Length[S]}]];

s=ErdoesRenyi[16,0.4];
{Ffunction[s,x],Curvatures[s,x]}
{Ffunction[s, x], 1+Total[Curvatures[s, x]]}
{EulerChi[s],-Total[Curvatures[s,x]] /. x->-1}

Author: oliverknill