We have seen that for a finite abstract simplicial complex $G$, the connection Laplacian L has an inverse g with integer entries and that $g(x,x) = 1-X(S(x))$, where $S(x)$ is the unit sphere of $x$ in the graph $G_1=(V,E)$, where $V=G$ and where (a,b) in E if and only if $a \subset b$ or $b \subset a$. We have also seen the energy theorem $\sum_{x \in G} \sum_{y \in G} g(x,y) = \chi(G)$ as well as a formula expressing the Euler characteristic as a potential theoretical energy of the spectrum of $L$. What are the other Green function entries g(x,y)? Here is an other piece to the puzzle. A simplex $x \in G$ is called a facet, if it is not contained in a larger simplex. What is special about facets is that the unit sphere is a sphere.
| Theorem: if $x \in G$ is facet in G and $y \in G$ is any simplex contained in x, then $g(x,y) = \omega(y)$. |
This generalizes the already known general formula $g(x,x) = 1-\chi(S(x))$ for the Green function values in the diagonal in the case of facets because if $x$ is a facet, then $S(x) = \delta(x)$ is the boundary, the codimension 1 skeleton of the simplex and $1-\chi(S(x))= \omega(x)$. This allows for an easier proof of the formula ${\rm det}(L(G)) = (1-\chi(S(x))) {\rm det}(L(G \setminus \{x\})$ which is Cramer. We only need to look at the Laplace expansion of the determinant with respect to the new row. The result also gives us a faster proof of the result that the number of positive eigenvalues of $L$ minus the number of negative eigenvalues of $L$ is the Euler characteristic of $G$: this formula follows from a generalized multiplicative Poincaré-Hopf result which was a part in the talk about the energy of a complex, where I had to cut a corner.
Removable simplices
We have seen that every simplicial complex is more generally also a CW complex: it can be built it up $G_{k-1} \to G_{k}$ recursively by adding sets in such a way that every $S(x_k)$ in $G_{k}$ is a sphere. The construct of a discrete CW complex similarly, like $\Delta$ sets or simplicial sets, is a generalization of the concept of an “abstract finite simplicial complex”. While CW complexes are more general, every simplicial complex is a CW complex, there is a CW ordering $x_1, …, x_n$ of the simplices. We mean with this an ordering such that $S_k = x_k \cap \bigcup_{j-1}^{k-1} x_j$ is pure of dimension ${\rm dim}(x_k)-1$. The reason is that in a CW complex G, each unit sphere $S(x_k)$ is even a sphere, which is pure of dimension ${\rm dim}(x_k)-1$.
We have a bijection of simplices with eigenvalues of the complex such that positive eigenvalues correspond to even dimensional simplices and negative eigenvalues correspond to odd dimensional simplices, but this bijection can not be canonical. We need some kind of ordering of the simplices. The complex $K_2$ for example has an obvious $Z_2$ automorphism greoup symmetry, but the eigenvectors of $L= \left[ \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ \end{array} \right]$ do not share this symmetry as the eigenvalues are $1,1-\sqrt{2},1+\sqrt{2}$. We know that there must be two positive eigenvalues as there are two even dimensional simplices $\{ \{1\}, \{2 \} \}$ and one negative eigenvalue as there is one odd dimensional simplex $\{ \{1,2\} \}$. But while the two zero dimensional parts $\{1\},\{2\}$ of the complex can not be distinguished, we can associate one with the eigenvalue $1$ and one with the eigenvalue $1+\sqrt{2}$.
Let us call a simplex x in G “removable” if its unit sphere $S(x)$ (as a set) is a simplicial complex. (Note that in general, we define $S(x)$ as the complex generated by the set unit sphere.) Not all simplices are removable. For example, for $G=K_2 =\{ \{1,2\},\{1\},\{2\} \}$, only $x=\{ 1,2 \}$ is removable. For $x=\{1\}$, the unit sphere is $\{ \{1,2\},\{2\} \}$ but that is not a simplicial complex. Any facet is removable. I guess that more generally, if $x$ is removable, then $g(x,y) = 1-\chi(S(x) \cap y)$. I currently believe that one can generalize the above result to removable simplices and hope that it gives way to find in general an interpretation of the Green function values $g(x,y)$. At the moment, I believe it could be that the Green function values in general have a formula which involves Euler characteristic of subsets of a complex G which are in general not subcomplexes.
Shellability
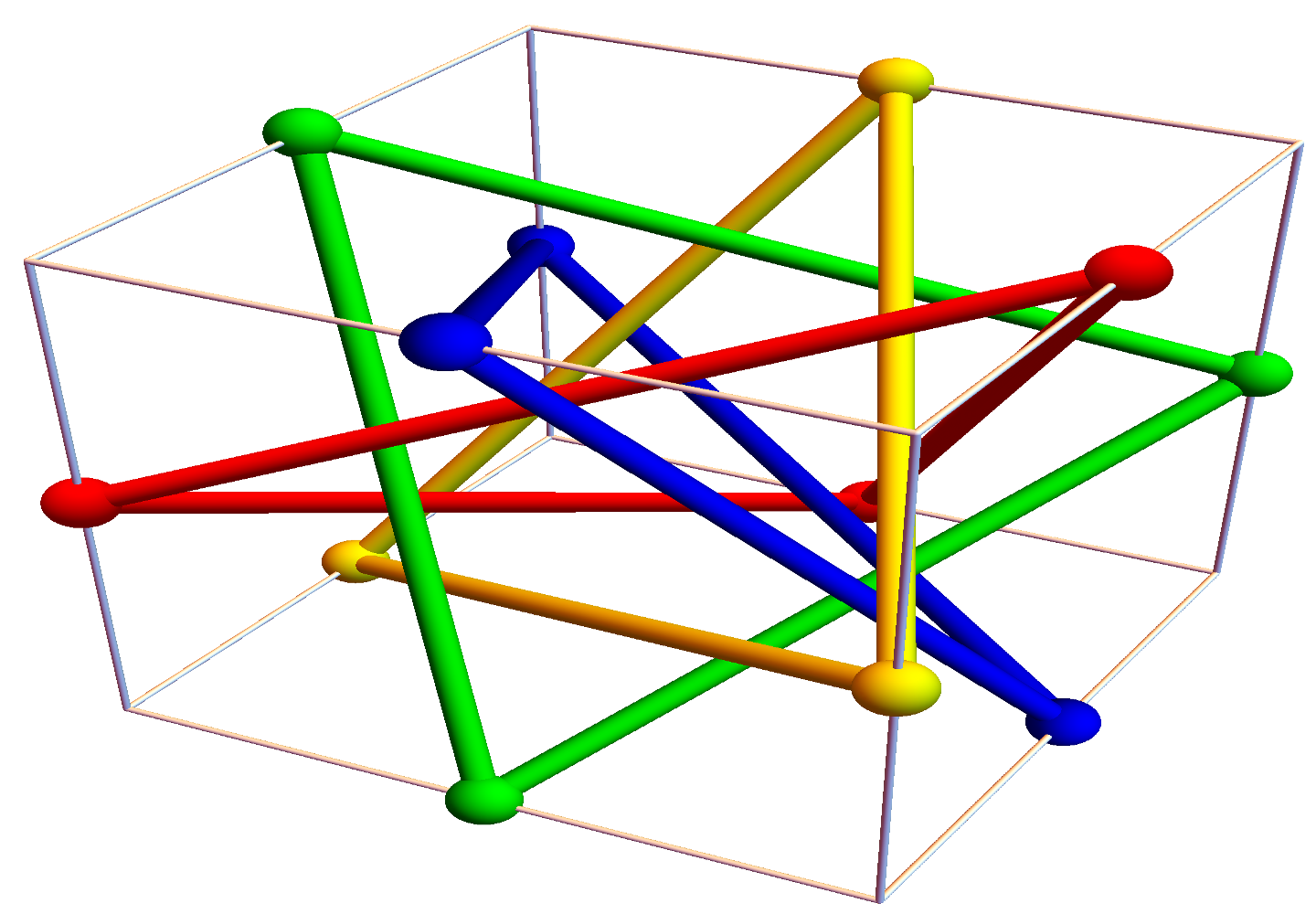
If the facets $f_1,… f_m$, the maximal d-simplices in $G$ can be ordered such that $S_k = f_k \cap \bigcup_{j-1}^{k-1} f_j$ is pure of dimension $d-1$, then $G$ is called shellable. Every simplicial complex is a CW complex but not every $G$ is shellable. The question which complexes are shellable is interesting. Mary-Ellen Rudin (1924-2013) (see photo) showed in 1958 that there are non-shellable triangulations of the tetrahedron. It has 41 smaller tetrahedra and 14 vertices. Guenter Ziegler found an example of a non-shellable 3-ball with 10 vertices and 21 facets. Already in 1924, Furch found an example of a non-shellable 3-ball, the “knotted hole ball”. Felix Frankl constructed in 1931 a tubular neighborhood of the dunce hat. Ziegler in his book constructed triangulations of cubes he calls Danzer cube. Ludwig Danzer (1927-2011) was an expert in polyhedra. Here is a redrawn picture of the Danzer cube as seen in Ziegler’s book:
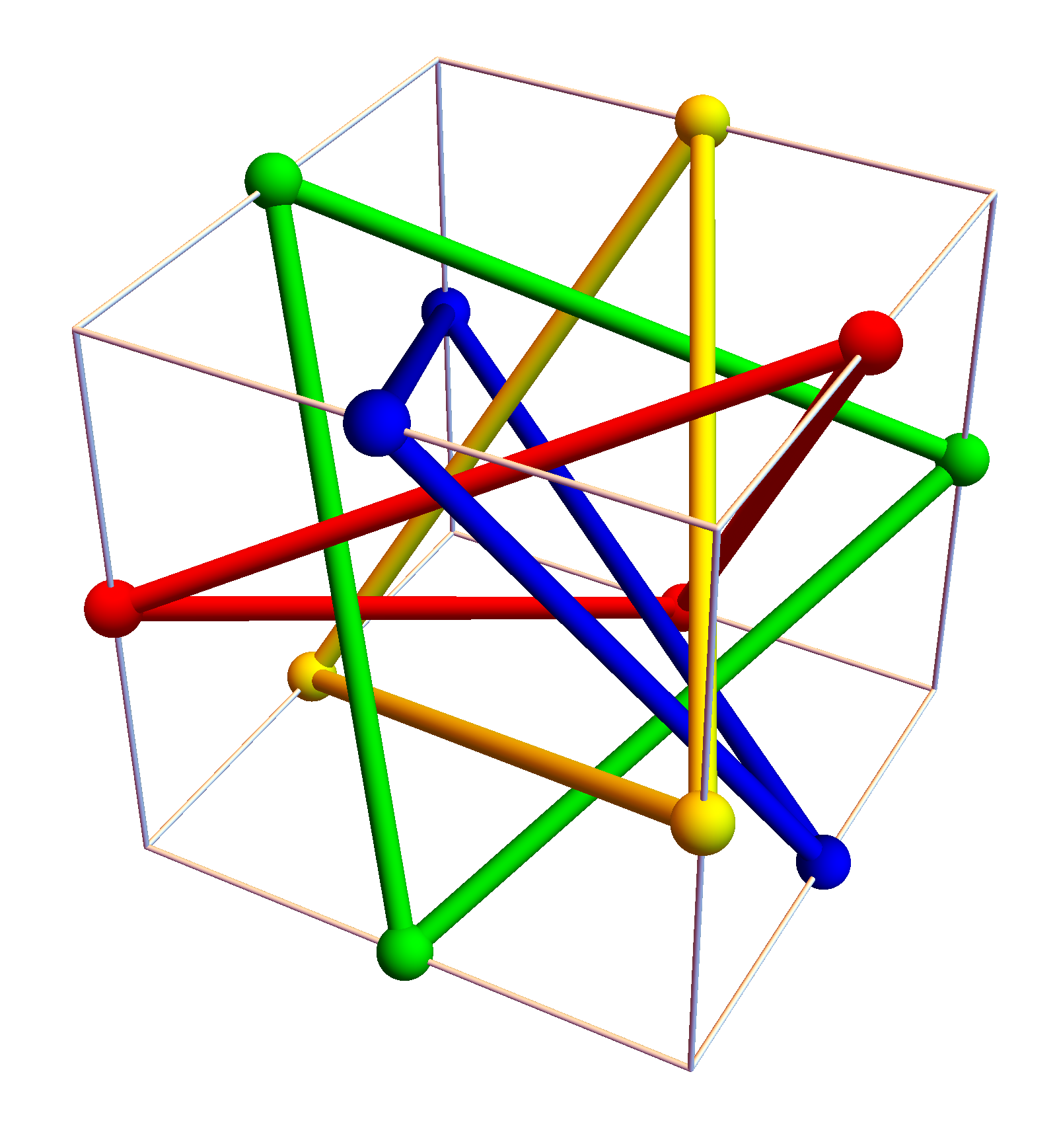
It can be completed with more vertices to be a triangulation of the cube which is not shellable. For us, shellability of a complex does not really matter yet. But it could be that shellability allows to say more about the spectrum of $L$.