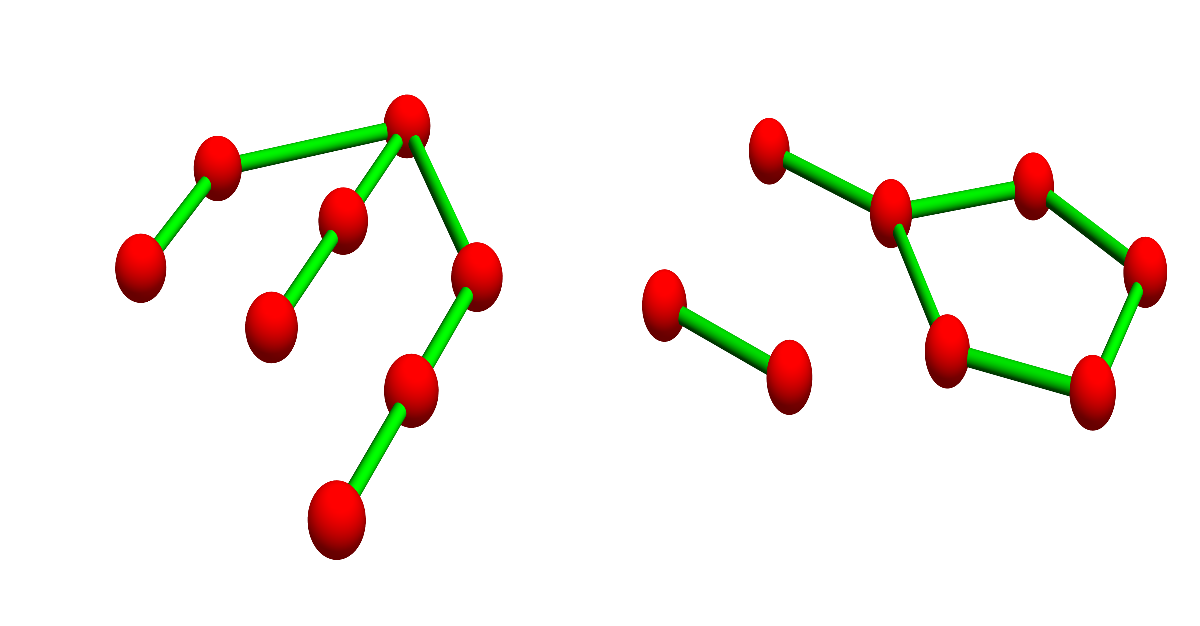
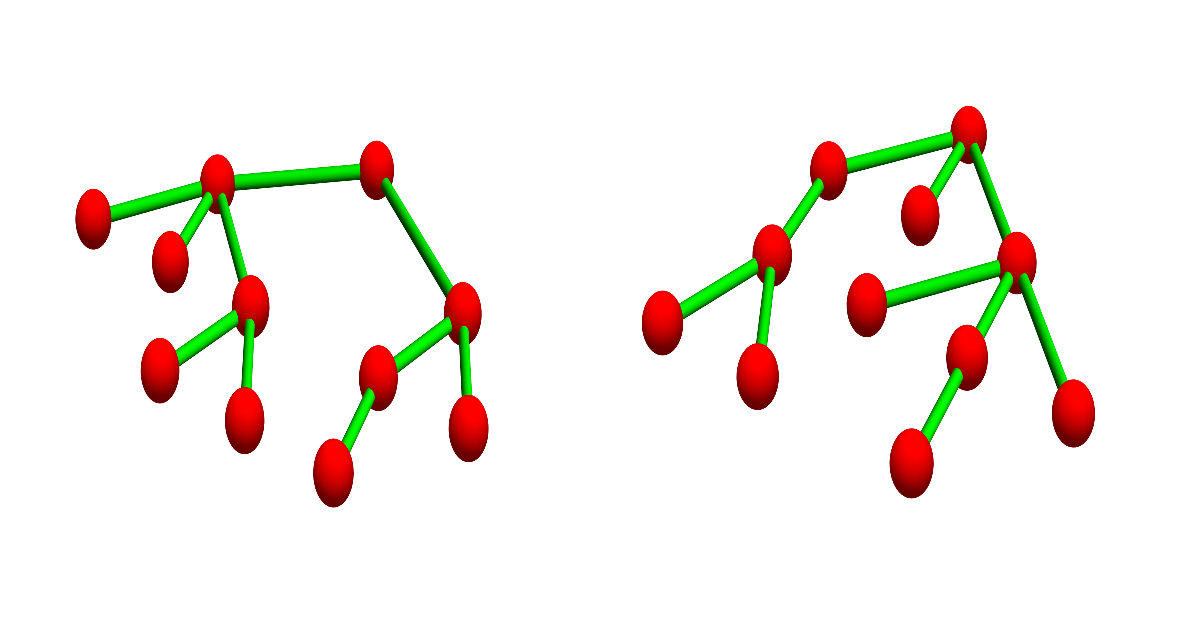
One can not hear a complex!
After some hope that some kind of algebraic miracle allows to recover the complex from the spectrum (for example by looking for the minimal polynomial which an eigenvalue has and expecting that the factorization reflects some order structure in the abstract simplicial complex), I wondered whether there is an argument proving that that there must be isospectral simplicial complexes? One can try to use the Pidgeon hole principle by counting the number of complexes and the number of possible characteristic polynomials. We thought then that there is a simple counting argument to show that there are of isospectral complexes. The counting idea was to compare the number of complexes with a given cardinality (Dedekind number) with the number of possible characteristic polynomials. One can easily see by looking at the connection matrix that the number of complexes with n elements must be bounded by $2^{n^2}$, the number of 0-1 matrices of size nxn. We have to work harder to estimate the number of possible characteristic polynomials. A rough estimate gives $2^{n^2 \log(n)}$ which is larger. One can certainly cut this down a bit by estimating the size of the coefficients of the characteristic polynomial more carefully but it is not obvious whether a simple Pidgeon hole argument proves collisions for the hash function “characteristic polynomial”. The argument did not work out but it gave hope to start a search with a computer. This search was successfull:
|
|
Example 1
The first example is a pair of one-dimensional complexes with characteristic polynomial $-x^{15}+15 x^{14}-84 x^{13}+198$ $x^{12}-71 x^{11}-471 x^{10}+528 x^9$ $+438 x^8-666 x^7-300
x^6+357 x^5+$ $185 x^4-58 x^3-56 x^2-13 x-1$. The left complex is a tree with Betti numbers (1,0,..). It is isospectral to a non-simply connected, not connected complex with Betti numbers (2,1,0,…).
Example 2
The second example is a pair of trees with characteristic polynomial $-x^{21}+21 x^{20}-176 x^{19}+724 x^{18}-1299 x^{17}-417 x^{16}+5179$ $x^{15}-4579 x^{14}-7319 x^{13}+11255 x^{12}+6049 x^{11}-12825 x^{10}-4479$ $x^9+8415 x^8+3483 x^7-2883 x^6-1879 x^5+163 x^4+412 x^3+136 x^2+19 x+1$.
CW complexes
Having examples of non-homotopic complexes (Example 1) and connected examples (Example 2), one could ask about higher dimensional examples. This could be harder to find by brute force computer search but the above counting argument shows that there must be many.
If one works in the larger class of CW complexes where one can take the product of complexes (in the strong ring), then it is now easy to construct higher dimensional examples. If A is isospectral to B and C is isospectral to D, then AxC is isospectral to BxD. One still has to be careful not to get isomorphic examples by accident. For example: if C=B and D=A, then AxC is isomorphic to BxD even if the pairs (A,B) and (C,D) are not isomorphic.
Further questions
November 5, 2017: as the spectrum does not determine the complex, one can ask whether the knowledge of the eigenvectors does. It is a corollary of the spectral formula expressing the Euler characteristic as a logarithmic energy (a consequence of the fact that positive eigenvalues match one to one with even dimensional simplices and that we can uniquely assign an eigenvalue and eigenvecdtor to each simplex), that we can realize every of the n simplices of G as a vector. We can therefore, given an order of the simplices (for example given by a build-up as a CW complex), assign to every simplex a point in the projective space P(n). The next question is now whether this point cloud determines the simplicial complex. In order to do that we have to look at relations between eigenvectors. So far, we don’t see any structure. But the probability that the eigenvector point cloud in the projective space determines the geometry is much larger. There is currently only intuitive support for the believe that the eigenvectors (without any ordering and knowledge of eigenvectors) allow a reconstruction of the complex. This intuition has a physical base: the eigenvectors live in a Hilbert space representing in some sense a quantum mechanical incarnation of the basic building blocks of space. Their structure might determine the geometry.
If we would have also the eigenvalues, then obviously we can reconstruct the Laplacian L from the spectral theorem: just use the eigenvectors to build an orthogonal matrix U, then define the diagonal matrix D with the eigenvectors inside and form $U^* D U = L$.
| The question is whether we can do without the knowledge of the eigenvalues. |
Quantum complexes
An other question we can ask is: how large is the set of unitary nxn matrix U and a diagonal matrix D for which $\log|D|=0$ for which $U D U^*$ has entries which add up to an integer? For the original connection matrix L, the energy theorem assures that the total potential theoretical energy $E = \sum_{x,y} g(x,y)$ is the Euler characteristic $\chi(G)$. The orthogonal matrix U defined by the eigenvectors and the diagonal matrix given by the eigenvalues belongs to the class. But if $L$ is deformed unitarily, then this energy changes and we have an energy E(U) which depends on U. As $E(U)=\chi(G)$ is a hypersurface in the unitary group, it is large dimensional manifold. We can now also look at the subspace for which the eigenvalues agree with the eigenvalues of L. Also this should still be a large dimensional connected space within the unitary group as we have only n conditions. Looking at the geodesic flow in this manifold produces now some kind of quantum mechanics and the motion of a basis in this flow determines a motion of a geometric object generalizing the concept of a simplicial complex. The standard integral theoretic concept of “index averaging” allows now to define a curvature for each of these generalized “quantum complexes”. What is also not clear yet whether such a generalized simplicial complex still has a cohomology. Fantastic of course would be if the isospectral Lax deformation of the exterior derivative would play some role here. But it could be even more interesting if there was a new cohomology generalizing the standard simplicial cohomology of the simplicial complexes and see that this cohomology changes evenso the Euler characteristic does not.
