Mandelstuff - Quantum Calculus

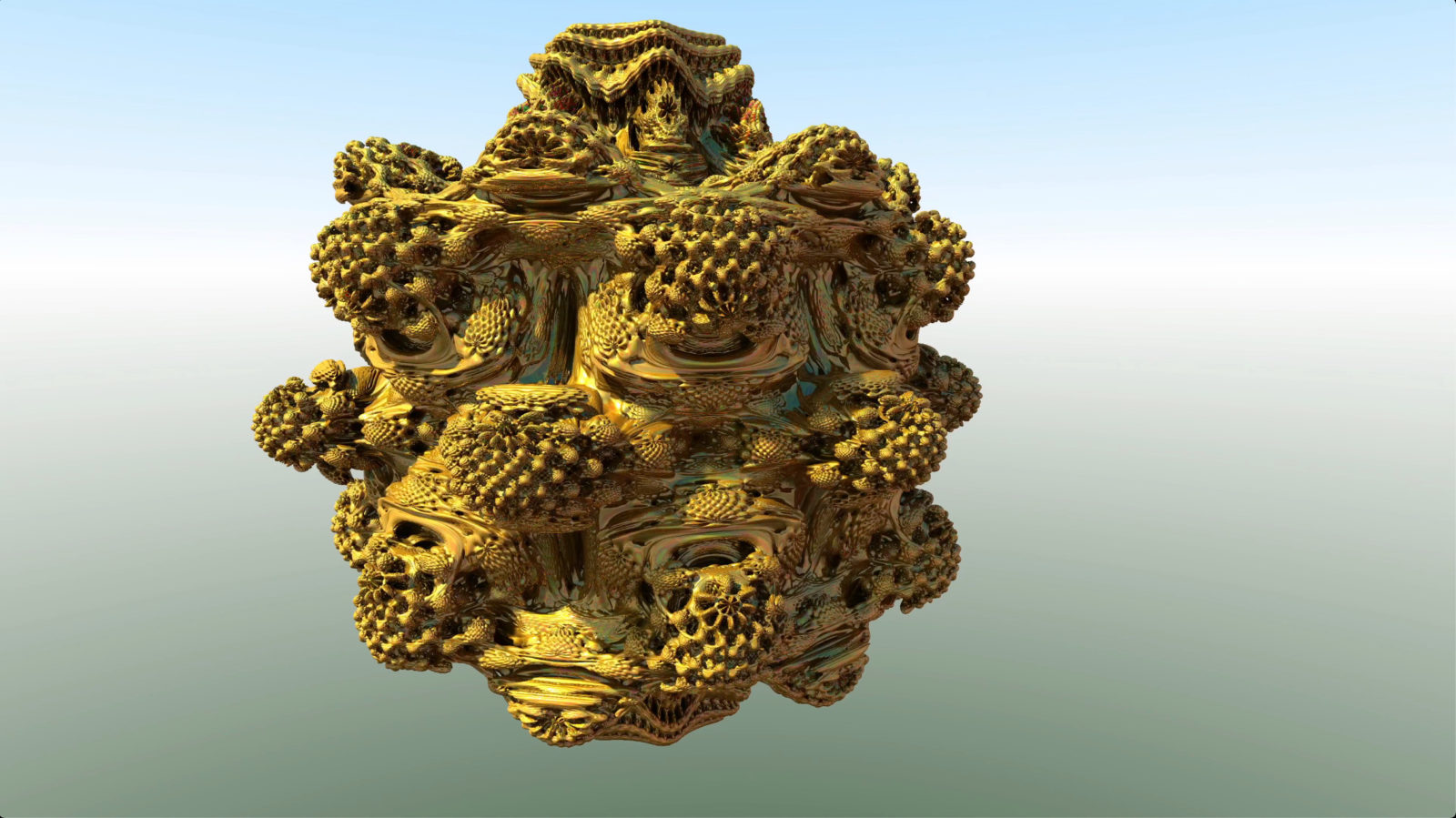
Mandelbrot hyped in 1982/1983. As a first year student, I had spent almost all my free time programming on early Apple computers. At that time, students would work mostly in labs [I still had still a cheap Tandy imitation at home with audio tape backup and Basic programming language] but on the Apple II, we could use floppies (!) and program in Pascal]. I saw the first picture of the Mandelbrot set when one the students in the lab there built a program showing off pictures. Soon after, one could see folks running around with Benoit Mandelbrot‘s “Fractal Geometry of Nature”. In a Moser-Seminar of around 1984/1985, (we had to participate in a couple of such seminars as requirement for the Diplom), Jochen Denzler presented the Douady-Hubbard proof of the connectivity of the Mandelbrot set. I myself got assigned a multi-dimensional complex dynamics linearization result of Rabinowitz, which actually turned out to be really nice. [I was a really arrogant prick at that time: when Moser passed me that paper of his former PhD student Paul Rabinowitz (typed up with a type writer and where Moser wrote in big letters Rabinowitz), I complained to him at first that this topic is “too old fashioned”. Moser was amused, objected and of course he was right: multi-dimensional complex dynamics got really hot later on). I myself really got “sold” on the beauty of fractals with Peitgen and Richter’s book “Beauty of fractals”. In my thesis under the guidance of Oscar Lanford, I worked in one of the chapters on almost periodic operators whose spectra are on Julia sets. It also led to an encounter with p-adic math as the almost periodic operators appearing there are actually defined on the compact topological group of dyadic integers. I would use the proof of of Adrien Douady and John Hubbard (as learned from Denzler) later in the classroom, first at Caltech (1995) and later at Harvard (2005). About 10 years ago, the first pictures of the Mandelbulb appeared and videos started to mesmerize. Strangely, mathematicians did not jump onto it. Maybe because it is too hard? Maybe because the set-up is not so pure (the set depends on the parametrization and so is not coordinate free? Maybe because the origin of the Mandelbulb is rather humble having been created by programmers, hackers, science fiction writers, musicians, artists, engineers, or folks hacking in various such things at once (Rucker, Ruis, White, Nylander). The Mandelbulber allows now everybody to do such movies. In 2012 project of Liz Slavkovsky brought me closer to 3d printing (see a related “From the Sphere to the Mandelbulb” from 2013) for which I had contacted Rudy Rucker and Jules Ruis some early pioneers in that matter. Daniel White and Paul Nylander (unfortunately, I had not been aware of Paul’s work yet in 2013) were finalizing and naming the Mandelbulb definition between 2007 and 2009. The video below is about Mandelstuff triggered by teaching spherical coordinates. It looks like a distraction from Quantum calculus, but not as much: one can define Mandelbrot sets a very general setting: for any family of dynamical systems, a point 0 and an escape set B,one can look at the set of parameters for which 0 does not enter B. This is the Mandelstuff of the system. In a ring, one can take the family $T_c(z) = z^d+c$ , where the degree $d \geq 2$ is an integer parameter. In Euclidean space $\mathbb{R}^m$ , one can look at a parametrization $U(\phi)$ of the unit sphere and write every point $x$ in spherical coordinates as $x= |x| U(\phi)$ and define $x^d = |x|^d U(d \phi)$ which of course is not a power operation in a ring. The Mandelbulb is defined using $U(\phi,\theta) = (\cos(\phi) \cos(\theta), \cos(\phi) \sin(\theta), \sin(\phi))$ . This is the most common White-Nylander Mandelbulb with most popular choice g=8. Some Mandelbulbers use the standard parametrization (where $\cos(\phi))$ and $\sin(\phi)$ are switched) which is also one of the templates in the program. By the way, the Mandelbulber program allows to explore any of those and much more!. In the video, the most obvious statement appears:

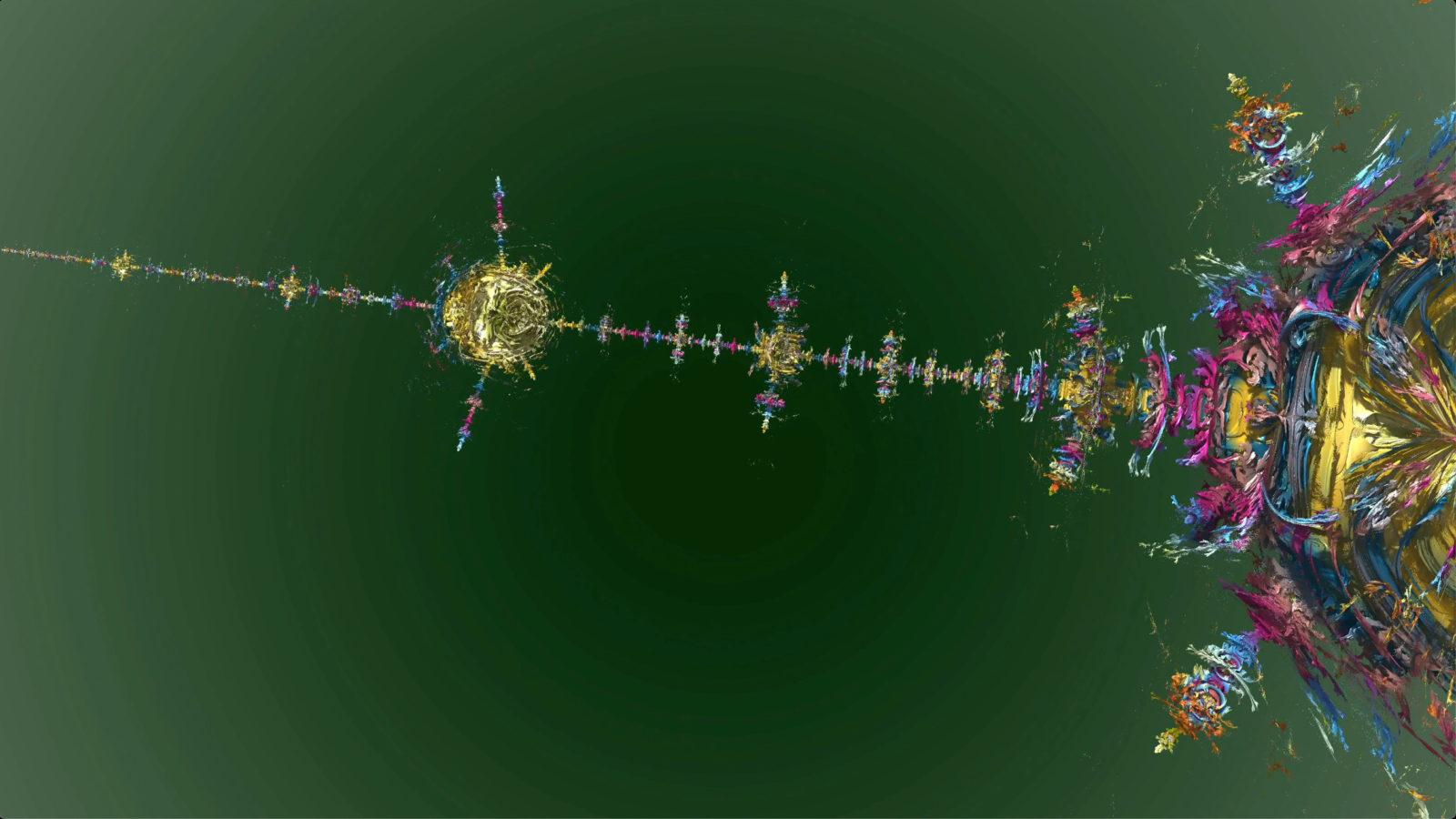
A slice of the degree d White-Nylander Mandelbulb is the degree Mandelbrot set.

It is an open problem whether the Mandelbulbs are connected. Actually now (as of morning of September 13th 2022), I believe that one should be able to prove the connectivity of the Mandelbulb using the Douady and Hubbard result (as of evening September 13, 2022, I still think so but that the proof is much harder than anticipated in the morning), I might look at this a bit next Saturday. It will most likely fail, like 99 percent of all stuff one starts in mathematics. But a bit of naivity can be helpful when doing research. It is also important to know why something is hard. That gives insight, even if one is unable to prove things.

Why posting this in quantum calculus? Because I’m in general interested in how to translate things from the continuum to the discrete. If one can not work with discrete finite mathematics to deal with fractals, then the “finitist approach” to mathematics is doomed. We know that one can do everything also in the finite, simply because the pictures of the Mandelbulb are all done all done on a finite “computer” containing finitely many bits. Most of modern mathematics is is much more adventurous. There are even developments which go far beyond the ZFC axiom system. Already Alexander Grothendieck went beyond ZFC when talking about universes. Current developments in categorical mathematics do not bother, since it is believed to be irrelevant. It probably is.

Still, all mathematics which uses the infinitely axiom is not safe from crashing at some point. I would not be surprised if somebody would prove one day that any axiom system which explicitly postulates infinity and has some minimal content like postulating the integers, must be inconsistent. And as I have pointed out quite a few times on these pages, this would not be a problem. We can work well with finite mathematics. Every computer scientist “feels” that. We are finite creatures, we can process only finitely many thoughts and symbols, measure only finitely many data. Infinity is a language construct which allows us to write some things down more conveniently. The burden of proof of the finitist however is to show that traditional mathematics like the mathematics of the Mandelbulb can be done also within a pure frame work of finite mathematics without using the crux of Euclidean spaces. This has not happened yet in practice. It happens theoretically in radically elementary approaches for example by compactifying a space and using non-standard analysis to deal with it as a finite set (Nelson’s radically elementary approach). But what would be needed is to have a purely combinatorics finite proof of say the Douady-Hubbard result without invoking infinity. This is not so weird: we can approximate the dynamical systems by maps on graphs and also model the parameter domain using a graph. On every approximation level, we would need the parameter domain to be a connected graph. And all should also look natural and not just a numerical scheme. Numerical scheme descriptions are usually ugly. Even books on difference equations are not pretty. Differential equations have much elegance. We are far from getting to this elegance using combinatorics alone.

In any way, here is a picture of the degree 2 Mandelbulb using the parametrization in which the equatorial xy-plane can be identified with the complex plane on which the map induces the quadratic map in $\mathbb{C}$ .

Author: oliverknill