Cool Inverse Problems

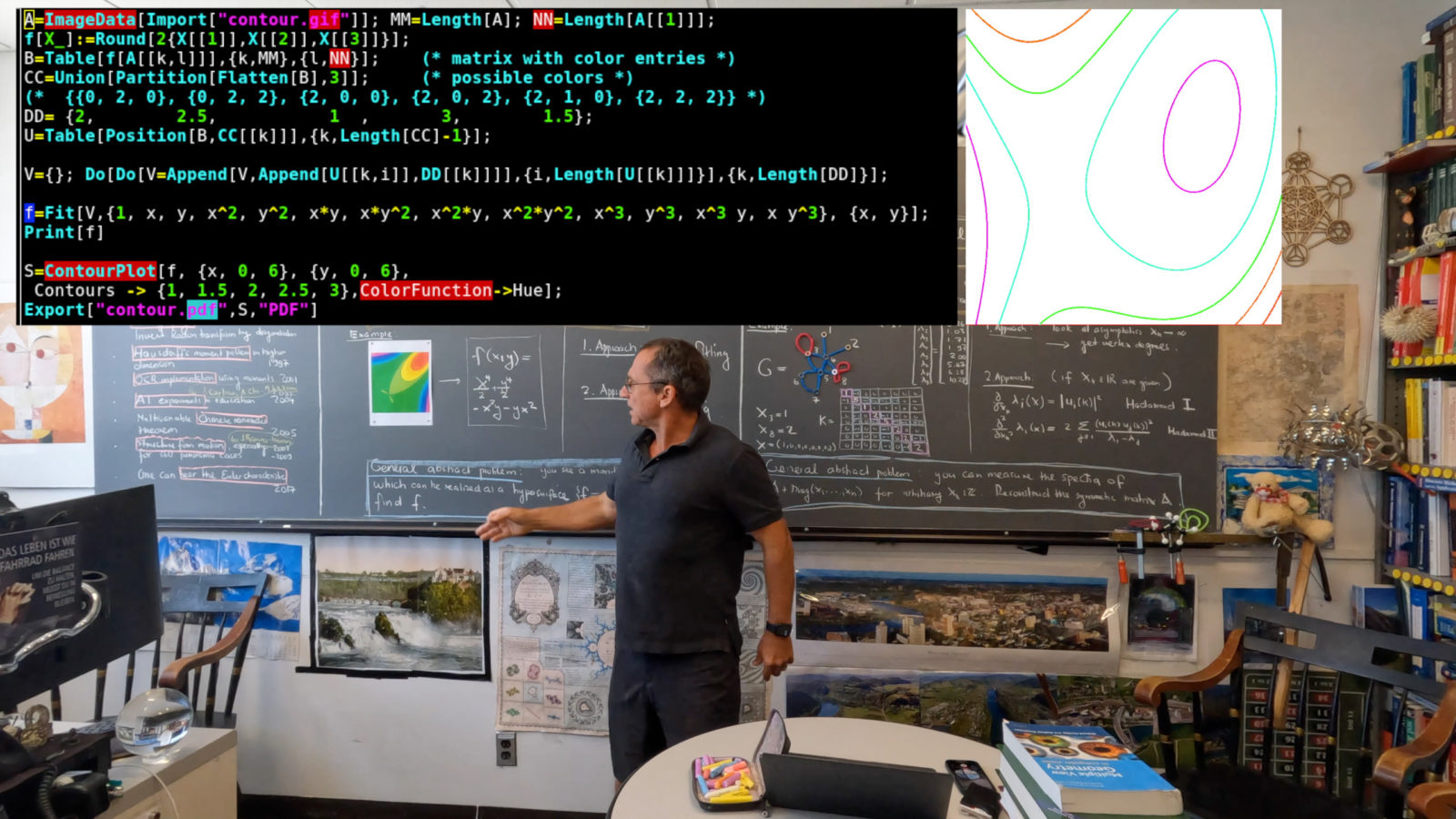
This week, I looked at two inverse problems. The first one emerged while teaching level curves in multi-variable calculus. The question is how to get from a contour plot a function f which produces that plot. The reconstruction can be done via data fitting but there might be better and more stable methods. The task is more elaborate as one might think at first. We need to locate the level curves and associate them with function values. I did this in an example by just manually determining some points, then also let the machine fit already colored level curves. An other think one might try is to build a database of known contour maps and then go from there, zooming in onto the parameter. More sophisticated would be to look at critical points, classify them and then reconstruct polynomials which have these critical points. In the example provided in the video, I used which has an interesting singularity at (0,0).

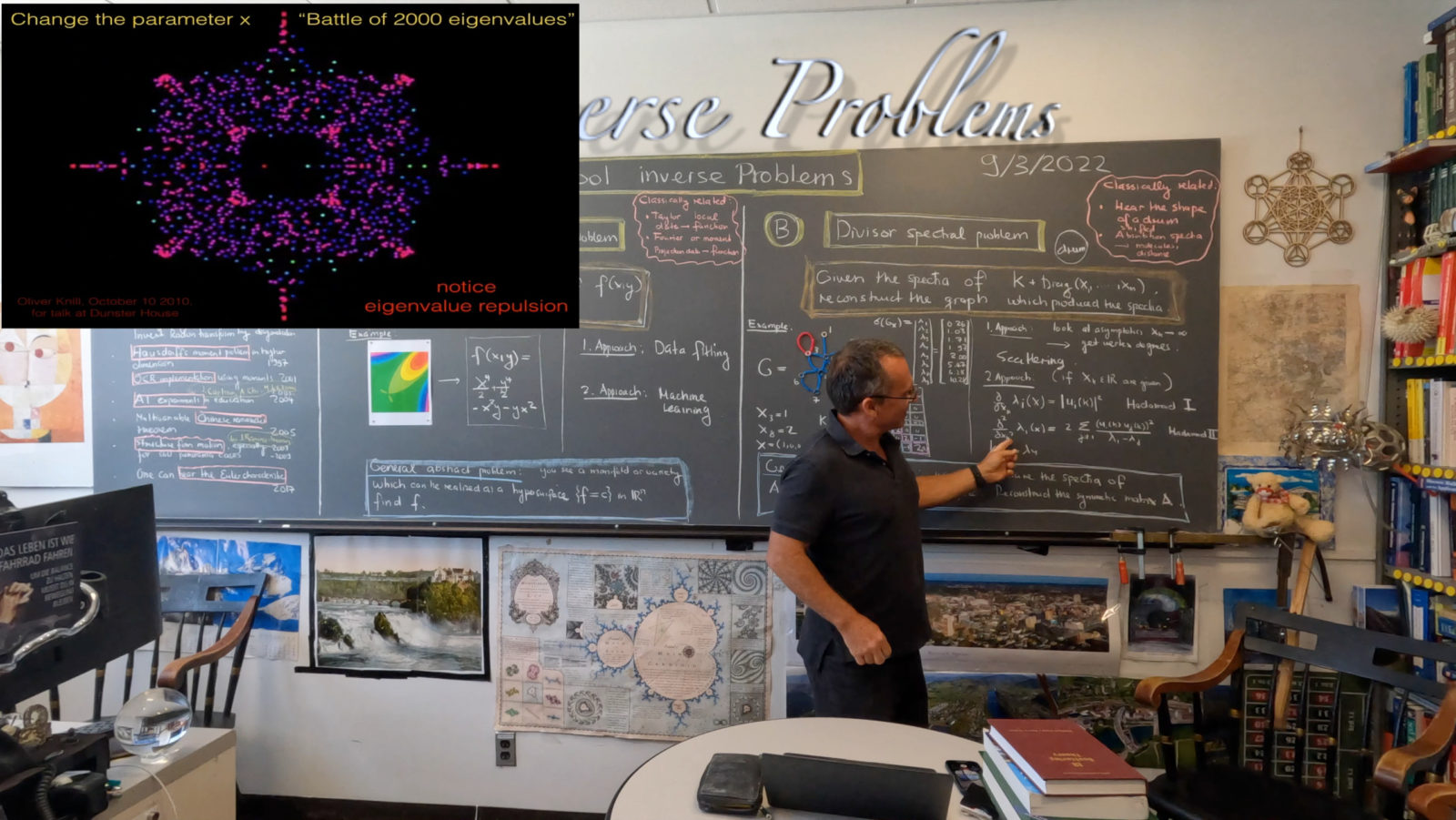
The second problem I was looking at is the task to reconstruct a graph if some quiver spectra are given. We mean with that that we are allowed to attach loops to the graph and measure the spectrum in each case. From these spectra, one should be able to reconstruct the graph. While talking, I did not know yet how to do it. I mentioned that it is possible to get the degree sequence by looking at the asymptotic behavior of the spectral radius if we attach a large number of loops at some node. I only later realized that this allows us then to get the spectrum of the adjacency matrix and from that it is not difficult to find out whether two nodes are connected or not by counting closed paths of length 4 as we have access to . Knowing also the adjacency matrix gives us then the graph. At the moment, I can reconstruct the graph with spectra if is the number of vertices of the graph. It would be nice to know whether one can reconstruct the graph with only O(n) spectra! It is not excluded that we can reconstruct the graph if the spectrum of one single cleverly chosen divisor X is known. We for now only know that we can not reconstruct in general with the zero divisor.

A more general problem asks how we can reconstruct a symmetric integer matrix A from the spectra of various cases of A+X, where X is a diagonal matrix. A quantitative question is: how many times do we have to look up the spectrum of A+X with some integer diagonal matrix X so that we can reconstruct the matrix A. Now this is harder. We can not get even the diagonal entries nicely. I mentioned in the talk an other approach: if we should know X for any diagonal matrix, not only real ones, we can use the Hadamard variational formula to get the absolute values of the eigenvectors. (the second Hadamard variational formula does not provide information on the signs of the eigenvector components). By probing the possible signs and checking whether they produce eigenvectors, we could in principle figure out the matrix.

This question can also be relevant in the famous “Can you hear the shape of a drum” problem which is still unsolved for convex drums G. Drums are convex, and the known counter examples are not convex. But one could try to replace the Dirichlet Laplacian L with which is a finite rank perturbation of the Laplacian. How many such spectra are needed to reconstruct the drum? It is again possible also here that for any domain G (also not convex), some divisor spectrum decides the shape of the drum.