More about the ring of networks

The ring of networks is not a domain

[Update June 13, 2017: after a literature spree, I know now that the ring is already known. The Zykov ring is the dual ring to the strong ring. A bit disappointing of course, but also exciting as we can add an other angle to a ring which has been well studied. So, in particular, while there is no unique prime factorizaton in general, there are classes of graphs known in which there is a unique prime factorization. But what really emerged from this is that the Zykov ring is actually an important ring as it has strong arithmetic (factorization properties), strong topological (compatibility with dimension) and strong algebraic topological properties (compatibility with cohomology). ] [Update June 12, 2017: News flash: I know now that the multiplication in the Zykov ring does NOT feature a unique prime factorization . This might look a bit disappointing, but maybe it is more interesting as it provokes the question whether some kind of ideal theory restores it similarly as in number fields. The story written earlier which follows after the picture will lead to the non-uniqueness (and the analogy to the Grothendieck ring in the continuum had suggested that) but it needs to be written down still. The example of the graph G=A.B=C.D with primes A,B,C,D (which are all pairwise non-graph isomorphic) has maximal dimension 5, has 63 vertices, 1302 edges and f-vector (63, 1302, 11160, 41664, 64512, 32768) and Euler characteristic 1=63-1302+11160-41664+64512-32768. The graph as well as all its prime factors are contractible (homotopic to the one point graph) and especially have Betti vector (1,0,0,…). To the right is a picture.]

Dualization of Zykov multiplication

We have seen in the previous post that the Zykov addition is the dual of the disjoint union operation on the category of finite simple graphs . What happens if we dualize the multiplication?

This is very interesting. The ring of networks has as a dual ring a multplication which is a hybrid of the multiplication in the tensor ring and the Cartesian graph product , two rings which reportedly both have been introduced by Russell and Whitehead. Now, as already pointed out before, both the tensor product as well as the cartesian graph product have defects in that they are incompatible with topological notions like dimension or Euler characteristic or cohomology. For the multiplication in the ring of networks, at least the clique number is a ring homomorphism from the ring to the integers. Now here is the kicker:

Proof. We can produce a homotopy from G x H to the Cartesian product. To do so, first make a Barycentric refinement of G x H, then collapse any refinement of the product of simplices x in G and y in H (which has dimension to a ball of dimension . Here is an illustration, where we have to collapse a three dimensional tetrahedron to a two dimensional disc on every “two dimensional cell”. The right hand side shows the Cartesian product, we have seen in the Kuenneth paper, where the product graph is the Barycentric refinement of a Cartesian product on discrete CW complexes.

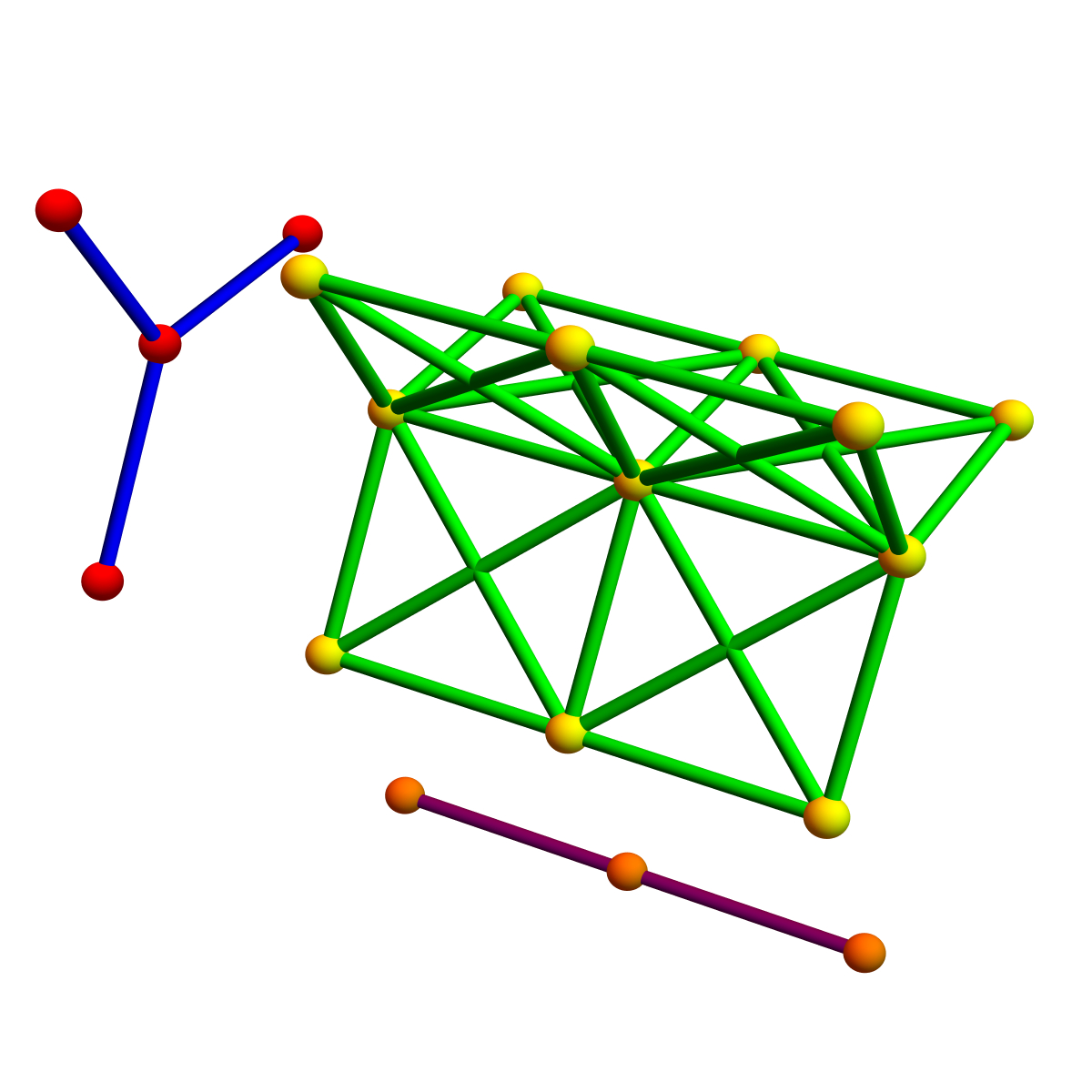
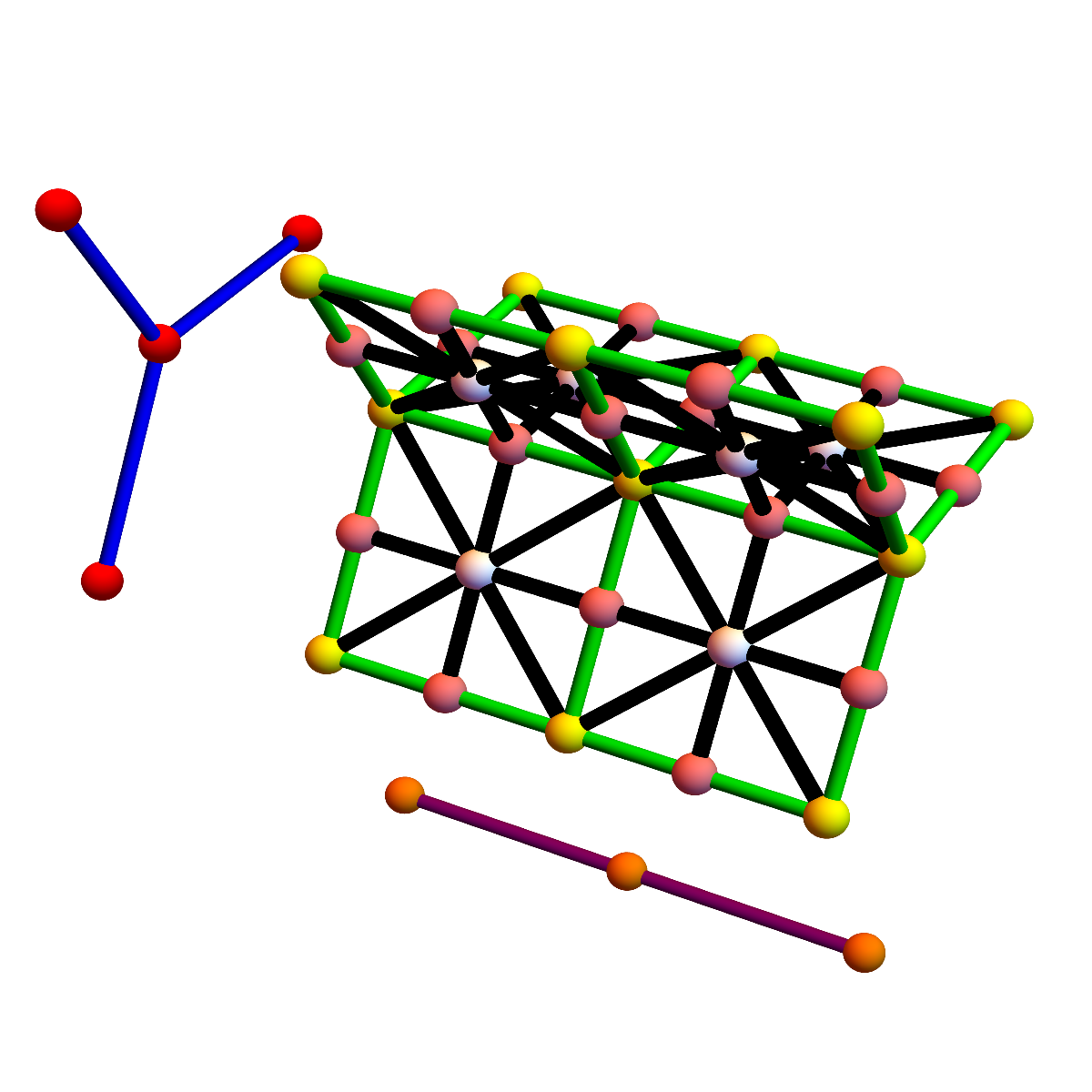
The dual multiplication essentially emulates a Cartesian product which is compatible with Kuenneth and Euler characteristic. But for that multiplication, we had to escape the category of graphs and even simplicial complexes and go to CW complexes. Or then – that is what we did in the Kuenneth paper – make a Barycentric refinement of the product for CW complexes to stay in the category of graphs, but destroying so associativity as already multiplying with K₁, the one element is a Barycentric refinement. Also the multiplication in the dual ring of networks has a defect. It is not compatible with dimension, but its dual twin does that for it! So, we can say:

It is a ring which binds them all, so to speak.

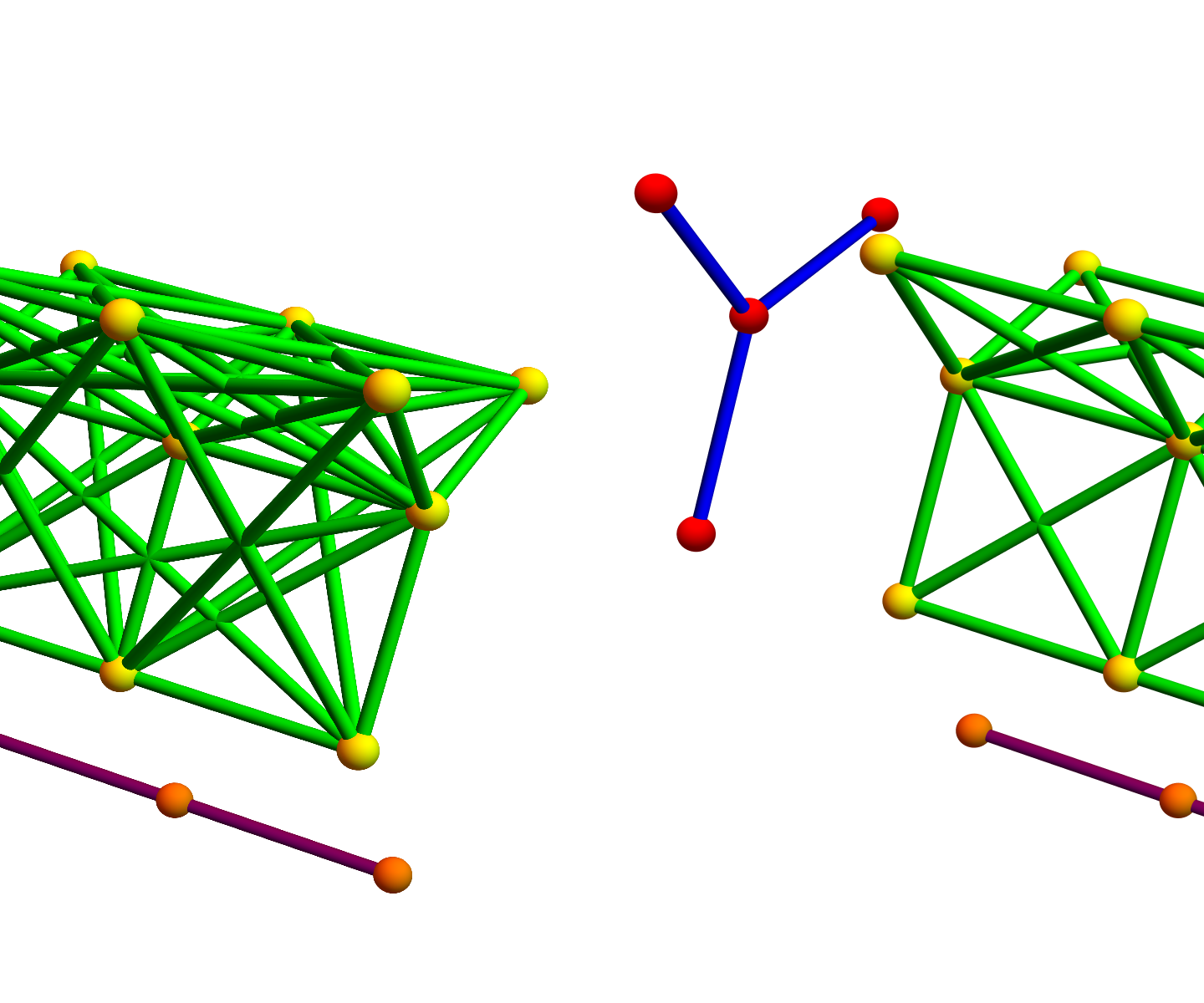
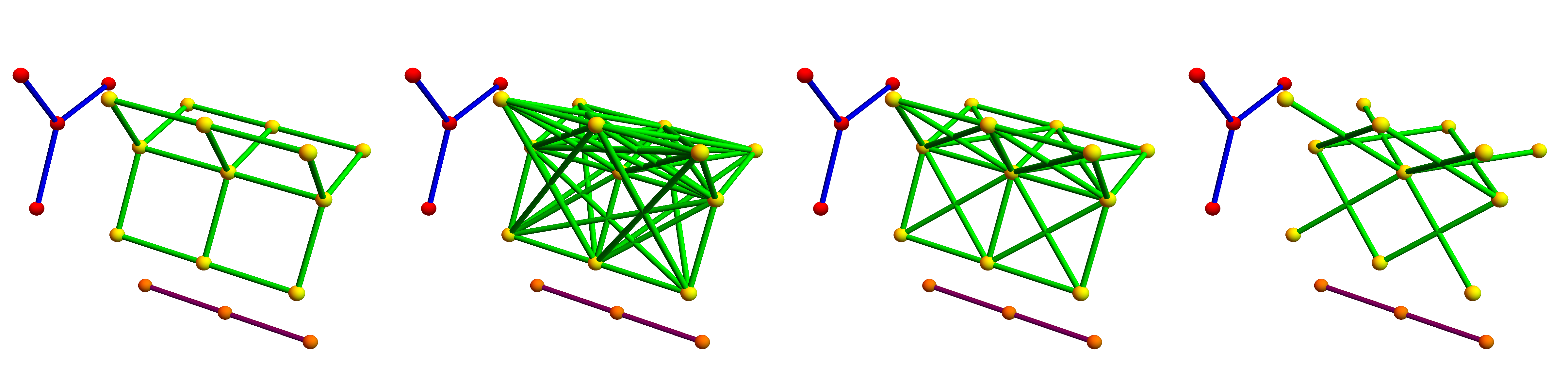
In the next figure, we see an illustration of four products. The first is the Cartesian graph product, the second is the new graph product in the ring of networks. The third is the dual product. The forth is the tensor product. We see that the dual product bakes together the Cartesian graph product and the tensor product (take the union of the edges). In all cases, we take the product of a star graph S(3) (with three rays) with a line graph L(2) (of length two).

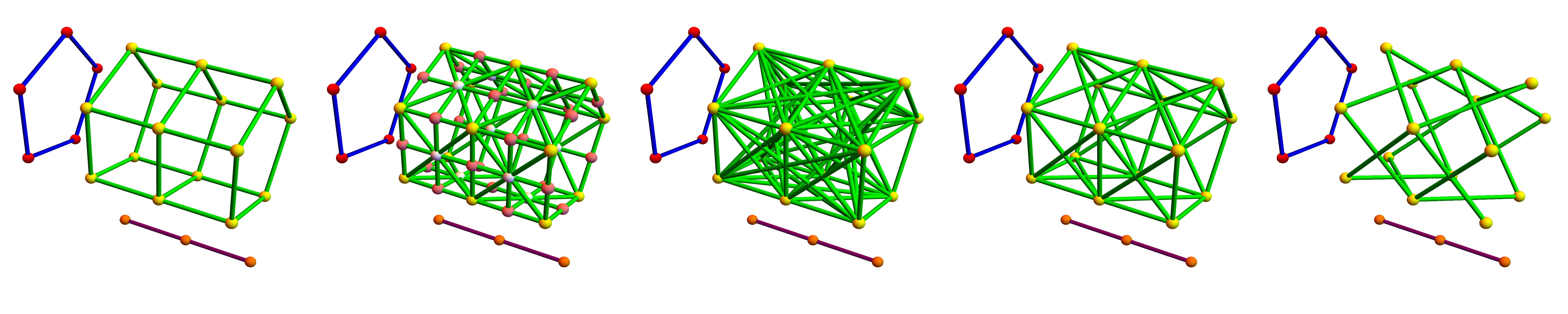
Here is an other example, where we take the product of a linear graph L(2) with a circular graph C(5).

The first product is the Cartesian graph product, the second is the Cartesian product (which by the way corresponds to the product in the Stanley Reisner ring which is also used to compute it. See the Kuenneth paper). Then comes the Zykov product compatible with the Zykov join addition. Then we see the dual of that product. We see it fills the holes of the Cartesian product with tetrahedra. The last product is the tensor product. The union of the edges in the Cartesian and Tensor product produce the dual product to the Zykov product. The second and fourth graphs (the Cartesian product and the dual Zykov product) are homotopic. This is the reason that while the dual Zykov product is a three dimensional complex, its cohomology and Euler characteristic is the one of the cylinder. One can see very well the defects of the graph cartesian product (the first one) and the tensor product (the last one). The fundamental group of the graph Cartesian product is already large (the Euler characteristic is V-E=15-25=-10 which can be seen that 10 holes were punched into the cylinder). The tensor product is not even connected. From a topological point of view, the product basded on simplices (the second one) is the best. Its dimenion is 2, and its cohomology is the one of the cylinder. We have seen that fixing the arithmetic properties (associativity), we have to go to the larger category of CW complexes.

Now duality also produces two new graph multiplications compatible with the Zykov addition: these are the dual operations to the Cartesian product and the Tensor product. As duality reverses inclusion, these multiplications are even fatter and have no compatibility with cohomology, dimension or Euler characteristic.

The big question is of course which of the rings have a multiplicative unique prime factorization. We are especially interested in the ring of networks. Of course, if this ring turns out to have a unique prime factorization, then also its dual has this property (and vice versa). It seems that the dual multiplication could be easier to analyze.

Now this dampens a bit the hope for the property to hold as the Grothendieck ring (for varieties at least) has no unique prime factorization. One also knows that the graph Cartesian product fails to have unique prime factorization.

Still we are in a combinatorial finite setup, where some combinatorial rigidity could hold which is not present in the continuum.