Unique prime factorization for Zykov addition
Graph theory

Unique prime factorization for Zykov addition

Unique prime factorization

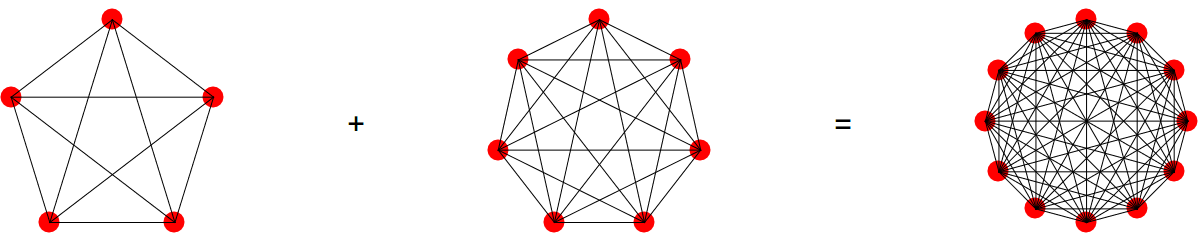
Let {{\cal G}} = \{ (G,V) \} the category of finite simple graphs. The Zykov join (V,E) + (W,F) = (V \cup G, E \cup F \cup VW) where VW is the set of all edges connecting vertices from V with vertices in W defines a monoid structure on {{\cal G}}. We have seen that there is a compatible multiplication \cdot which allows to get a commutative ring ({{\cal G}},+,\cdot). We have wondered about unique prime factorization of the ring. We know that this holds now and will give two proofs. Tutte, a MathReview reviewer claimed that Zykov already proved this in his paper (which is in Russian). The Harvard libraries could provide me with the article but probably due to language reasons, I could not find the statement there. Anyway, already the first proof is simple. The second proof will make it completely obvious.

The additive Zykov monoid satisfies unique prime factorization.

Proof. As the fundamental theorem of arithmetic illustrates, it is only really necessary to prove a Euclid type lemma. (While Euclid did not provide a full proof of the fundamental theorem of arithmetic, the rest follows by induction from that lemma. That Euclid did not have yet the fundamental theorem of arithmetic is a bit subtle and had only been realized by Andre Weyl). So, we only have to show that if A is prime and if A+B = C +D, then A=D or A=D. If this is not the case, then AD= A \cap D and AC=A \cap C are both not empty. But now, since every vertex in C is by definition connected to any vertex in D, we have A=AC + AD, where AC and AD are both not the zero graph. This contradicts the assumption that A was prime.

Here are some exapmles of additions.

Representing additive group elements

This proof does not tell us what the structure of the Zykov primes are. Before we give the second proof, which involves a concept which escaped us for months, let us state the important corollary:

In the group generated by the Zykov monoid, we can write every element uniquely as G = A-B, where A,B are both graphs.

Note that a priori, without the prime factorization, we don’t even know about the so called cancellation property which tells that if A+K=B+K, then A=B. Now, to compare this with the additive group of integers, we can always write an element as n or -n. This is no more true here. For example, if G,H are primes, then the group element G-H can not be simplified further. Concrete examples are G=C5 and G=C7. They both have prime volume and are therefore prime.

The reason why this was not an issue in the additive group of integers is that in that monoid the only prime is 1 and the prime factorization of an integer is 1+1+….+1. For networks, the addition is much more interesting. I had wondered in the spring in a blog entry here whether the prime factorization would be of any use for cryptology. We will just see in a moment that the answer is NO. We can very quickly verify whether a graph G is prime or not and also the prime factorization in the ring of networks is easy.

A dual group

The following idea was hidden for long. I’m happy however to have found the argument alone as this would be an instance, where, if pointed out by somebody else, one feels embarrassed after having thought about it for a long time.

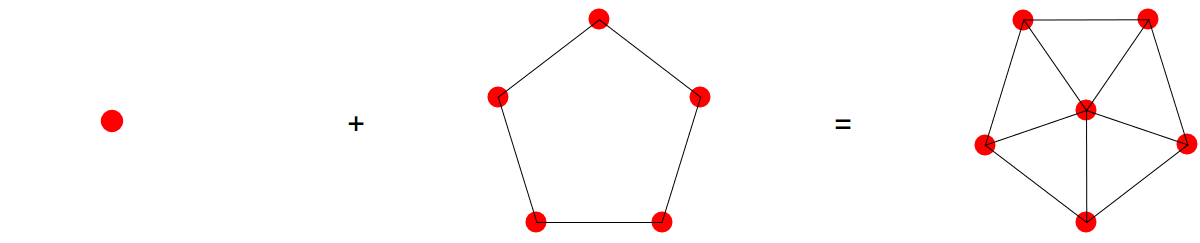
There is natural involution on the category of graphs. It is given by the process of taking the complementary graph. The complement of a graph G=(V,E) has the same vertex set V like G but we take the missing edges \overline{E} in the complete graph over V as vertex set of \overline{G}. The complement of the point graph Pn (a graph with n vertices and no edges). is the complete graph Kn. Here is the important lemma

The disjoint union operation \cup is conjugated to the join operation +. The conjugating map is the complement operation.

Proof. We have just to verify G + H =\overline{ \overline{G} \cup \overline{H}}. There are three type of edges in G + H. Edges in G, edges in H and edges connecting vertices from G and H. In each case, we can verify that it appears on the other side. Take e in E(G) for example. Then it e is not in \overline{G} and so also not in \overline{G} \cup \overline{H}. But then it is in \overline{ \overline{G} \cup \overline{H}}. The second case where \in H, is similar. The third case is, where the edge e connects a vertex a \in V with a vertex b \in W. This is on the right side because such an edge is not in \overline{G} \cup \overline{H}. The opposite direction works the same: start with an edge on the right hand side and verify that it is in G + H. QED.

It follows:

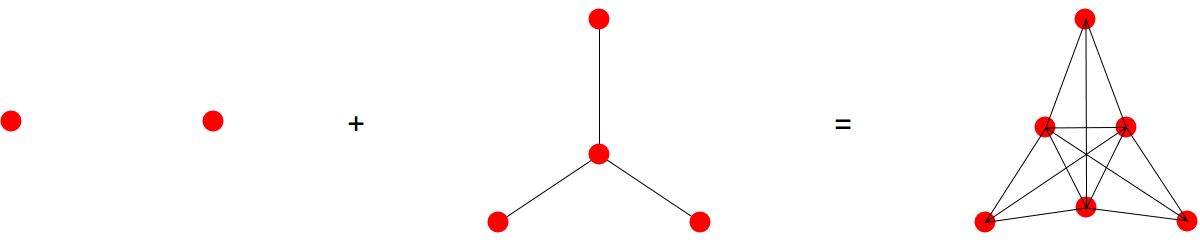
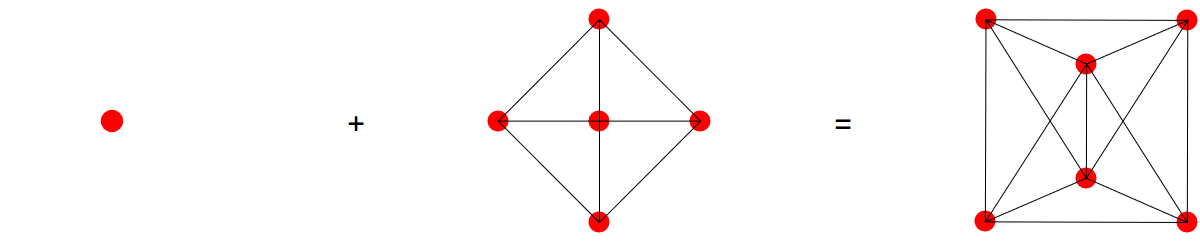
The primes in the additive Zykov monoid are the graphs G for which \overline{G} is connected. The prime factors are the duals of the connected components in \overline{G}.

Example.
The wheel graph W(4) with 4 spikes is a cone extension of C(4) so that W(4) = P(1) + C(4). Now, since C(4)=P(2) + P(2), the prime factorization is P(1) + P(2) + P(2). There are three prime factors. Now, if we would not have known about the prime factors, how could we have found it? We could have looked at the complement graph which is K(2) \cup K(2) \cup K_1.