Natural Metric Groups

What is a natural arithmetic?

In 2008, I experimented with the following definition: a metric space (X,d) is natural if there exists a unique group structure (X,+,0) on X such that all group translations and are isometries of (X,d). A group is natural, if comes from a natural metric space. It is then a natural metric group (X,d,+,0). It had been a bit of a shock to me to see that the integers are not natural but that the dihedral integers (the half integers) are. Could it be that the famous Kronecker quote “The good lord created the integers, everything else is human made” has to be adapted to “half integers”? Does this mean that there an additive arithmetic that is more fundamental than the arithmetic of pebbles which has been developed since 10’000 years starting with counting sticks? We have seen with multiplication that non-commutative multiplication is much more fundamental than commutative one. But that insight only dawned to us with the emergence of operator algebras, quantum mechanics and non-commutative geometries. Nobody so far has questioned that the additive structure on integers is the most important one. Once defined on the natural numbers where it forms a monoid, one group-completes it to an operation on , then localizes to build the rational numbers, the completes in a topological way to build the dyadic numbers or real numbers (this is by the way a place where metric spaces and arithmetic come together already), then completes algebraically to get the complex numbers, forms various algebras or rings beyond it like for example operator algebras. In parallel, one has also used finite structures like finite fields and extended this using various ideas like field extensions to produce number theory which goes far beyond the number theory of integers. We also have experimented with the Shannon ring and its completion. This went beyond the usual mathematics we deal with. It was is still based on pebble mathematics in the zero dimensional case. It also had been a commutative ring in a classical sense. Mathematics has built up a huge collection of structures but the arithmetic of the integers. As Leopold Kronecker famously pointed out was hardly ever questioned as the most fundamental of all constructs. This is also historically and pedagogically rooted, and what we do in school when learning mathematics is paralleled very closely to how humans have developed mathematics. Historically, humans have first started counting, then built number systems, linked it to geometry due to practical reasons. Addition and subtraction for example naturally comes up when trading stuff. Multiplication naturally comes up when computing areas or volumes. But similarly as we only learned that multiplication of quantities like position and momentum do not satisfy the law p q – q p = 0, it could be that fundamentally, there is something much deeper than integers available, something which does not satisfy p+q = q+p. So, here is a video which argues that there could be something more fundamental than the integer arithmetic which Kronecker thought about. Mentioning this was triggered recently by the need to look at half integers when looking at ultra-finite calculus notions. Also the half integer discrete complex plane is natural in this sense.

Statistics of life

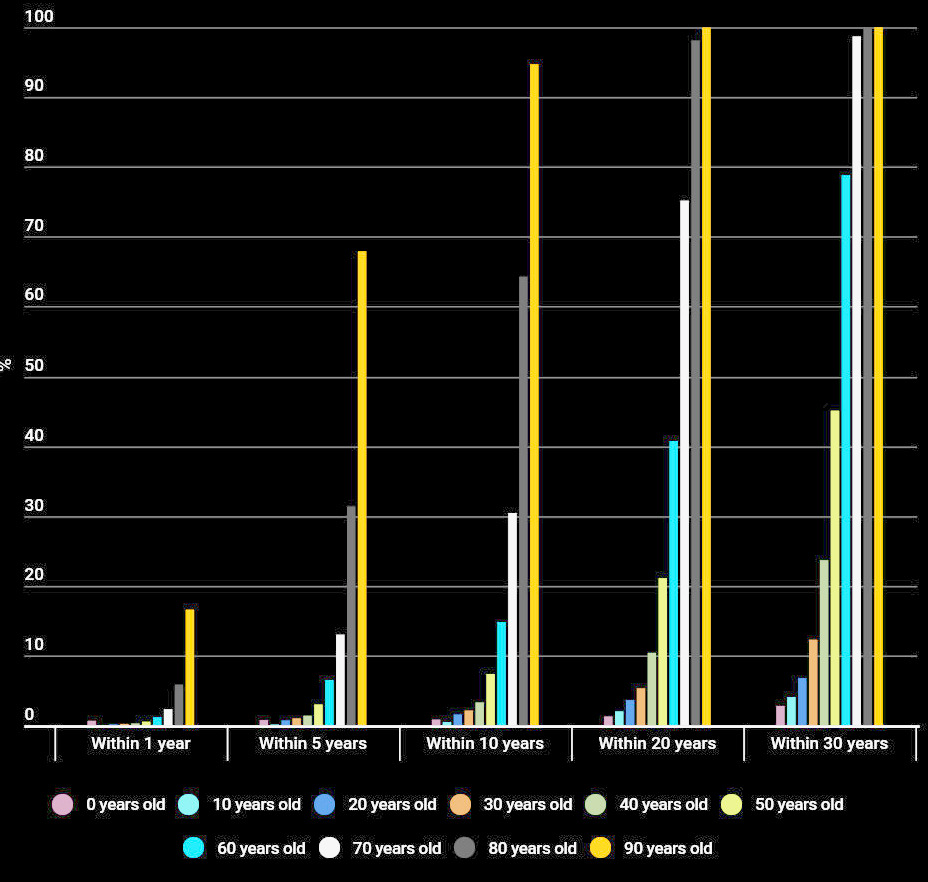
Here is an explanation why posting this. I count about 700 latex files in my research folder and have little idea what most is about any more. It would be a horror to see (from after life of course, as a junior research assistant to the all mighty), to have all my original ideas gone, whipped out and seeing from after life how some kid uses the recycled SSD hard drive to play games, having overwritten all my files. I’m a data person and like statistics. Actuaries publish life expectancy numbers regularly. The data from 2019 indicate that I soon will have a 10 percent chance of dying within the next 10 years. I’m not worried, ran about 5000 km last year and feel better than ever; but one never knows. It could be over tomorrow , there is a lot of probability involved. So, this video at least brings to live one of the ideas of mine which never saw the light. The idea of a “natural metric group” has originally been more ambitious. I wanted to look for metric groups such that the group determines the metric and the metric determines the group. The former is harder to do. Look at the real numbers for example. One can arrange the number line on a helix in 3-dimensional space and take the induced metric. This metric is clearly translation invariant but it is not the usual metric |x-y|. There are lots of metrics which are not equivalent and which are group invariant. If one insists that the metric is a Riemannian metric, yes, then one has essentially uniqueness up to a scalar multiple and all metrics must be of the form c|x-y| where c is a positive constant. So, there was quite a bit of thought and experimentation going into the definition. I mentioned in the movie that at that time, we had been interested in inquiry based learning techniques. It was also a bit an experiment with creativity. How do you come up with new notions in mathematics? This construct is definitely something new.