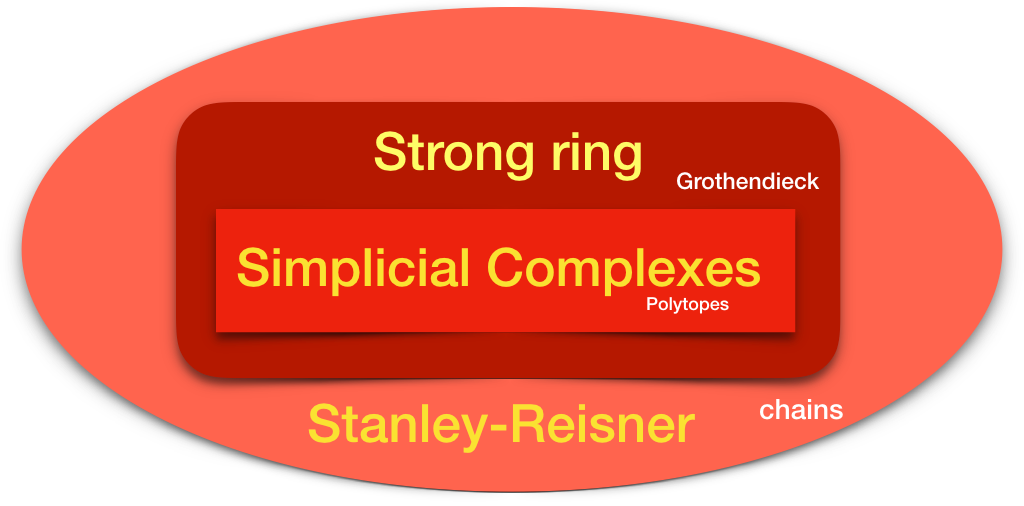
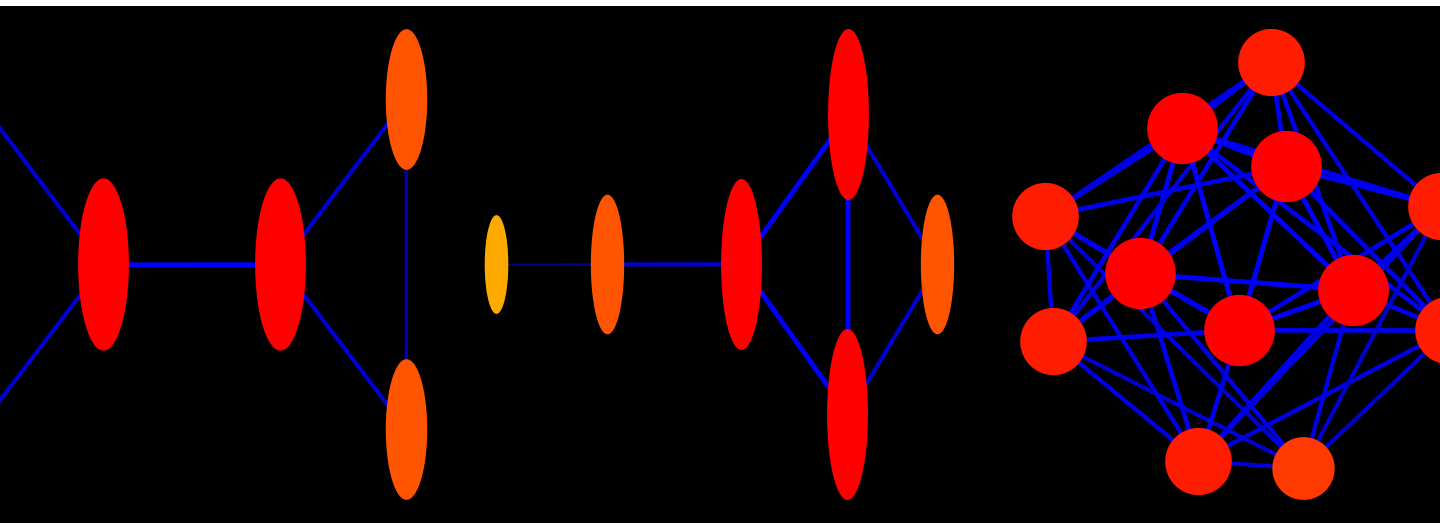
From Numbers to Particles
A nice thing about mathematics is that it has no dogmas, statements which have to be taken on good faith. Axioms come closest, but by nature also, they come with an honest warning that one can either accept them or not. Already Euclid fought with the parallel axiom. Today it …