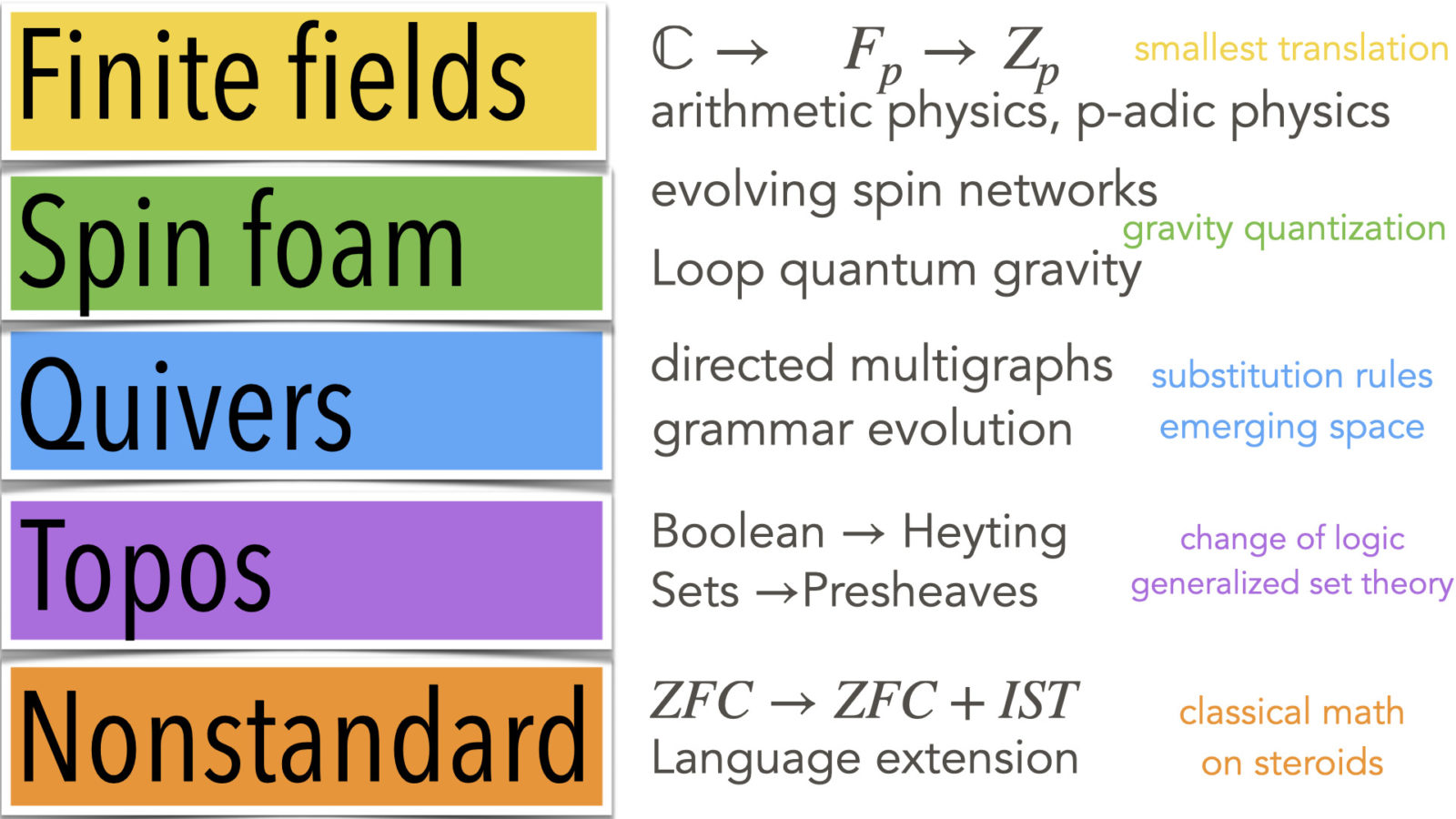
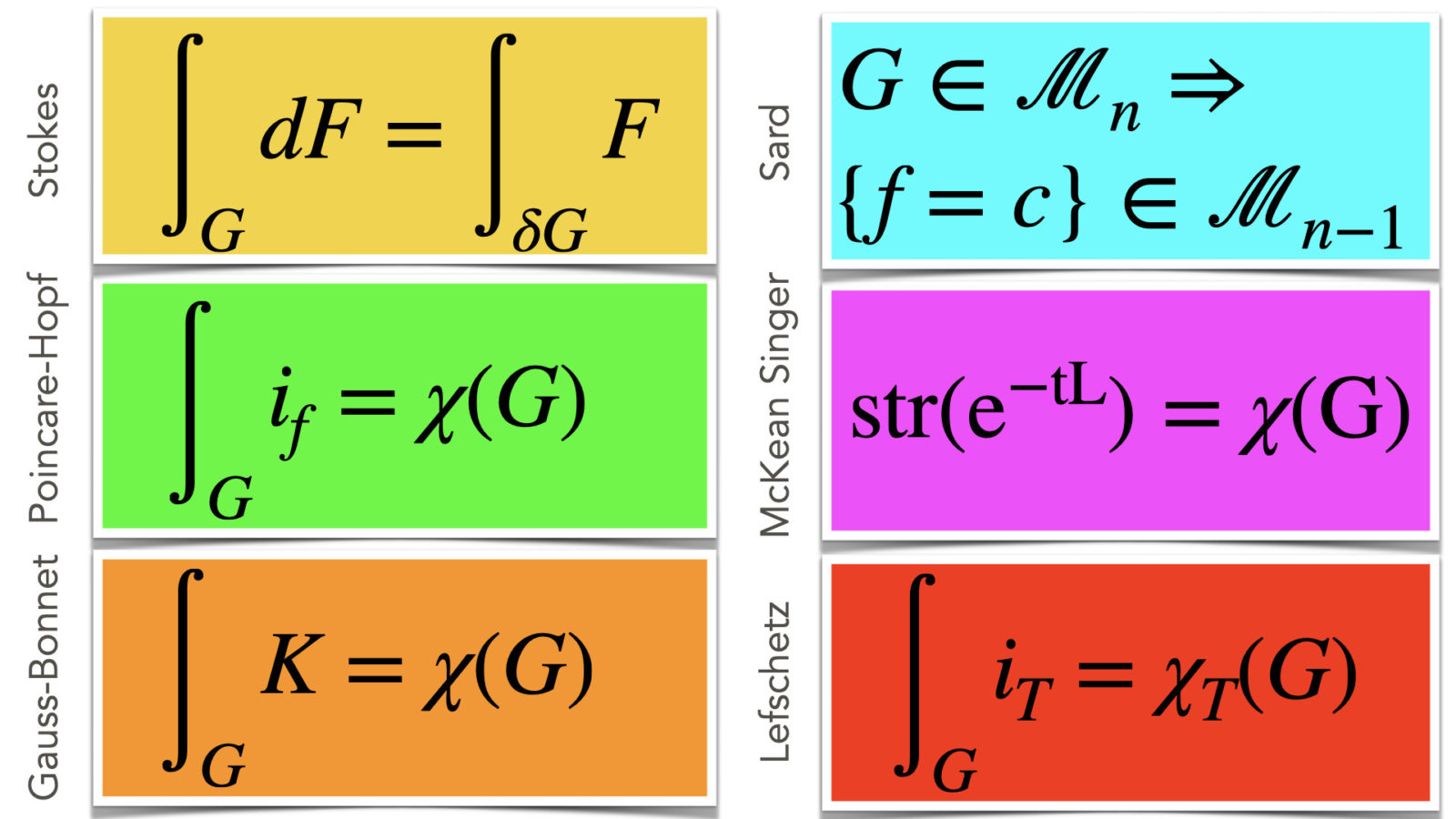
Here are a few slides presented on March 10, 2022 at a Wolfram physics seminar. I tried to explain a bit what I understand under quantum calculus.
[Update: 3/17/2022: A) summary videos about theorems: 10 theorems in graph theory, 10 more theorems in graph theory, 10 theorems about discrete manifolds.B) Related to Poincare-Hopf: my favorite version is for digraphs: “If G is a finite simple digraph with no triangular cycles then , where and is the graph generated by all neighbors of x pointing towards x. “ The notion of vector field enters in this formulation through the direction of the edges. C) During the talk the question came up why not formulate things over a lattice. The lattice is attractive in numerical schemes like in Lattice gauge theory. For me, the problem of computing determinants of the random lattice gauge field came up in spectral questions about Schroedinger operators. In 1D, the determinant encodes Lyapunov exponents, one of the enigmas in ergodic theory. Here is something about critical points of a quartic Lagrangian. ( PDF of the article). But assuming a lattice is already taking for granted to have a locally Euclidean structure of space. I like about the Wolfram physics project is that there are no a priori assumptions about the structure of space. Most theories assume the existence of an underlying Euclidean space. The quartic Lagrangian is next best approximation for the determinant. Determinants as a space time structure has difficulties because the corresponding Lagrange equations do not feature finite propagation speed and so no dynamics we can simulate. The quartic Wilson Lagrangian has critical points produce nonlinear wave equations which can be computed and evolve. On a space with 1 element, it is a cubic Henon map, on a finite graph it is a coupled map lattice. The Wolfram physics project still needs to single out a dynamics which can then produce data that compare to data from the real world. Having models which produce data inconsistent with physics is not a problem. It is just an object in the larger field of mathematics and not in the more narrow field of physics. It looks like String theory belong there. In the presentation, I quipped about Arnold’s “Math is the part of Physics where experiments are cheap” by reformulating it as “Physics is part of Math where experiments are expensive”. This is actually not a joke: as a mathematician you can create worlds which can not be observed, maybe because it is not rich enough like in flatland or then too hostile like in 4 dimensional space, the Newtonian Kepler problem is unstable and stars collapse. It is no problem however to simulate such worlds. Newtonian dynamics already singles out 3 dimensional space among Euclidean spaces. But why is space Euclidean? Why is it a manifold? Why is it not a variety or a scheme, an exotic topological space or a site, or a combinatorial object defined over a finite field? This is Kustaanheimo’s approach from the 1950ies. A mathematician is a game designer who can create worlds and games without having to worry that the game makes sense or can be sold. A physicist only deals with games which sell. And that can be expensive …. Billions and Billions of dollars, to bend a catch phrase of Carl Sagan. ]
P.S here is the Mathematica code tweeted a while ago and shown in the first part of the talk
The “Nature poem” of Emily Dickinson looks extremely naive but it addresses the basic question: what is nature, (or in modern terms: what is science?) Is it what we can see? Nay! It is more than that. Is it what we can hear? Nay! It is more than that. The answers are not bound to our senses. It is what we know. We have no art to ever explore it entirely as our wisdom is impotent to the actual simplicity. Still, the definite answer to the question is not limited to actual physical measurements but what we can explore theoretically using knowledge. My own take on this is (which is of course an interpretation from an other time and perspective) is that a mathematician can build worlds using knowledge alone without seeing nor hearing them. Even so most of these models are not visible nor audible (*), they are thinkable.
(*) Of course, for everything we think, we can also try to make it visible (by visualizing it or writing it on paper) or audible (by talking about it) even so it is not directly observed in nature. We have perfectly consistent and quite well understood theories about p-adic worlds or worlds built from hyper-reals for example even so nature might not have chosen them as basic building blocks (we don’t know of course and might never know because the scales at which they become relevant might not be accessible to us ever). But the mathematics is real and yes would exist also if nobody would have build the theories, similarly as the bumble bee or the bobolink would exist without humans observing them (Plato). In this talk however, I stressed also that it might be intellectually more honest to stick to finite mathematics (not accepting the infinity axiom) because everything we do, think, compute or measure is always finite. Then again, this choice, sticking to a Brouwer’ish simplicity might just be an idealization again and only exist as a thought construct. The question then of course is how could we ever prove that space is a continuum, if it were? What if we would establish up to a scale of ,(way beyond the Planck length scale ) that space is a continuum. Would it prove that it is so? — Nay, Yet we have no art to say. So impotent our Wisdom is! — Discreteness could kick in on a much smaller scale only. But we have to stay pragmatic also. The track record of combinatorics like Kustaanheimo’s finite field approach to explain things like the Newtonian motion used to navigate satellites or computing the eigenvalues of the hydrogen operator to explain the periodic system of elements or the differential geometric notions to use to explain gravitational wave patterns (quantitively!), is poor. I myself am just mesmerized how continuum theorems become so much easier in the discrete. I see the continuum just as an idealization or link to the actual physics which we will in the end be able to bypass. We are far from this however. There is no graph theoretical simple computation of the eigenvalues of the Hydrogen operator for example (even so I tried)!
