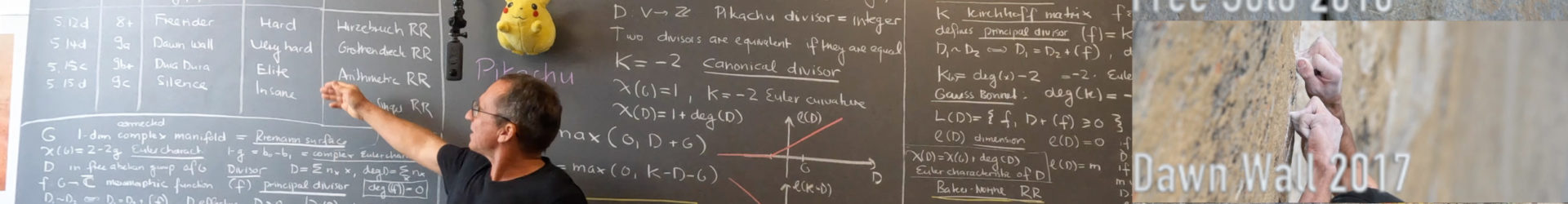About the video
Quantum calculus is a finite approach to mathematics. This can include geometry and even all of mathematics if one takes it seriously. The background question is very general: What one can do in mathematics without the infinity axiom? Why would we want to probe this? First of all because axiom systems which use infinity could be doomed in a very fundamental way in that they could be inconsistent. By Goedel, we can for sufficiently strong axiom systems not prove their consistency within the system itself. Most mathematicians are not concerned about this (including me) and pretend that we have a consistent system unless proven otherwise. So, we usually just ignore the question. But one of the things we can try to do is to replace given theorems in mathematics with finitist versions. This works beautifully in the case of Gauss-Bonnet, Poincare-Hopf, Euler-Poincare, Brouwer-Lefschertz, Riemann-Hurwitz or McKean Singer and in some sense already in Riemann-Roch. I talk here a bit about the Baker-Norine Riemann Roch but mostly about the most elementary case of Riemann-Roch, the case, when the space G is just a point. In this case, a divisor is just an integer and Riemann-Roch expresses the Euler characteristic of the divisor in terms of distances to the geometric object. It is good to think also in this way for the classical Riemann-Roch theorem.
About Pikachu
Having inherited a Pikachu doll recently when my wife Ruth moved her business office and needed to get rid of stuff, I dedicated this version of Riemann Roch to Pikachu. There is a long tradition of mathematicians to dismiss simple things as Mikey Mouse mathematics. One can see this as arrogance but it is also a bit justified, because mastering some serious mathematical topics needs years of dedication, study, learning, thinking. Some mathematicians work for many years on a rather special problem. Others gain fame by taking something rather well known and post it on youtube. It can be frustrating if you work thousands of hours on something and get a few dozen views while somebody takes a topic like the Euler formula, dresses it up nicely and gets a few million views. There is a reason, most folks can relate to simpler parts simply because it can be understood. Understanding something is the most exciting part of math. I’m not afraid of modern math but I have actually very little understanding of some of the modern notions, even so I learn mathematics for over 40 years and constantly make efforts to learn new things. There are some parts I can simply not understand yet like condensed mathematics. I guess that I’m probably not the only one who thinks that some of the modern mathematics is rather inaccessible. And the consequences are actually quite severe for the pure mathematics business: computer science, statistics and applied math eats away more and more from the more accessible mathematics. This is serious because it is related to funding. I have the maybe old fashioned believe that good mathematical structures should be poetry rather than a manual and that it should be possible to explain a definition in a few minutes. Poetry and Math like any art needs to remain accessible, otherwise it is doomed to be forgotten or ignored. To be fair, one must say that historically, much of the new mathematics that has been considered too abstract at first or inaccessible like set theory or point set topology or the notion of manifold or scheme but some have eventually sunk in. It is maybe like in any evolutionary system, the good stuff will survive, the less good will be forgotten. One does not have to worry too much about it.
About climbing
I compare that theorem to a Matterhorn climb, while modern versions of Riemann Roch are tough climbing problems like Dura Dura first explored by Chris Sharma and then climbed first by Adam Ondra. I like the analogy between climbing and mathematical topics because like Dura-Dura, there are topics of mathematics which appear completely inaccessible. But it is worth watching the documentary about that challenge. It needs complete dedication, many years of preparation, attempts, failings, support by others, collaboration to finally conquer the task. I like the analogy also from a pedagogical level as one can see also that solving such a problem is not possible without having the entire route memorized, every move, every grip, every little feature has to be completely inside the memory. The analogy is of course not really accurate. There are climbing routes like Dura Dura which would physically just be impossible for me due to smaller size body (there are many, many other limitations of course like lack of technique, mental state, strength etc which however to some degree can be trained). In mathematics, we do not know of basic physical limitations. The memory, number of neurons etc are pretty much the same for all humans for example. Apropos climbing: here is a spoof about the Dawn Wall. And here is a letter to the class of 2021, which addresses the question of risk and has two clips from the Dawn Wall and Free Solo movies.
About infinity
There is an other reason, why we want to get rid of infinity: it is academically honest to work with finite structures because we are finite creatures: we can measure, process and write down only finitely many data entries. A simplistic model of our brain treats it as a computer with finitely many possible states. This is maybe even true on a fundamental level if we look at quantum mechanics and the fact that energies are limited. Demokritus has speculated that matter is built up in atoms. I myself believe that he was just lucky. It could have come differently. There had been no evidence at that time (or wrong evidencew) that matter is composed of atoms. Ancient philosophers have also contemplated about the nature of space. Euclid wrote that a point is something which has no parts nor magnitude. All experiments we have done so far indicate that space is a continuum but this is just because we can not probe distances smaller than say 
The Planck limit
It is like working with real numbers on a computer in which the floating point arithmetic accuracy is 
