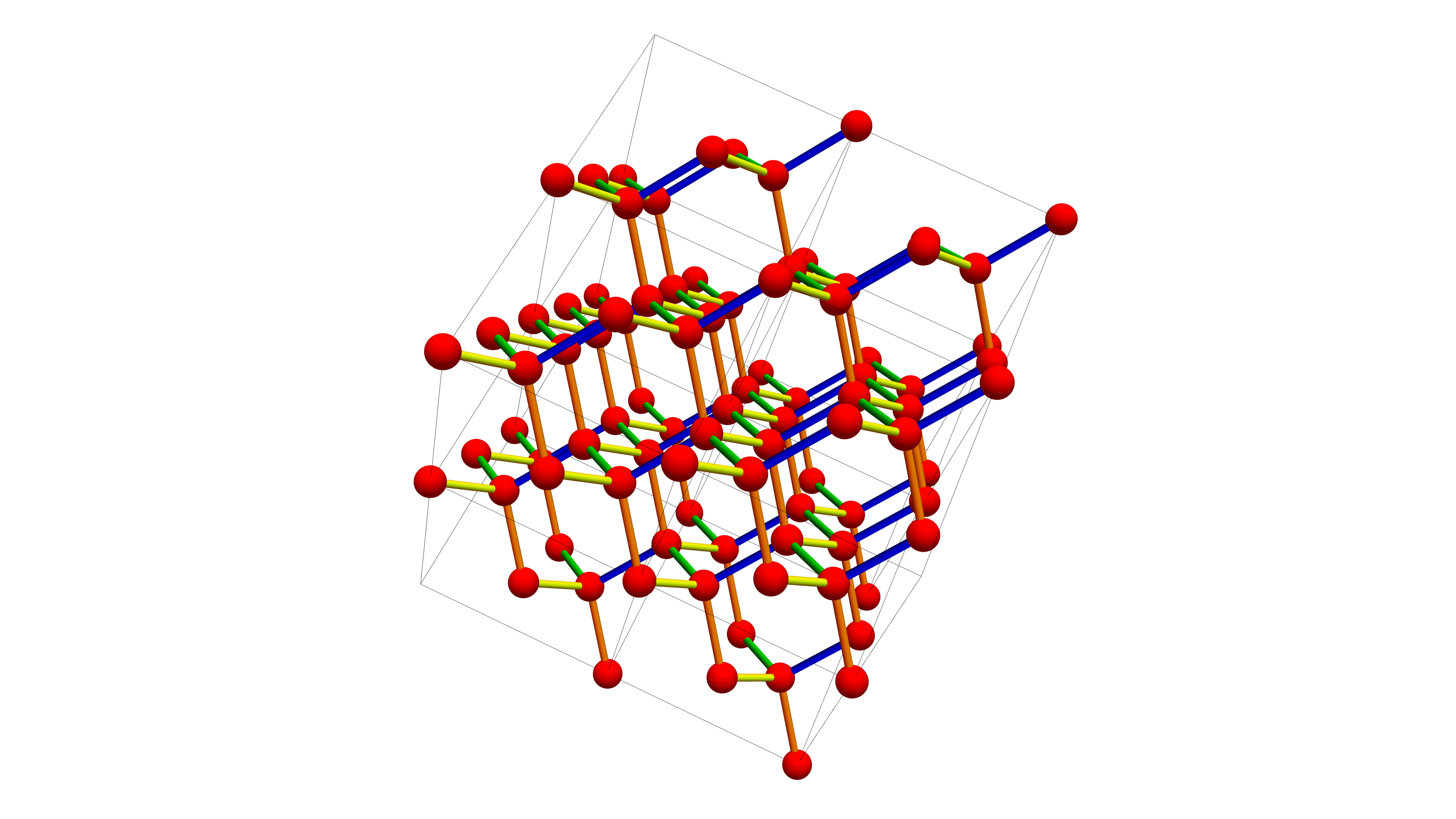
Here is the start of the novel “Schild’s ladder” by Greg Egan from 2004. It has sometimes been called the hardest SciFi Novel. Indeed, you can already be stuck in the first paragraph. The text describes the diamond lattice (there is a Wolfram demonstration file here by Sandor Kabai from 2008). I used that code to produce the graphics to the right, mimicring the picture shown in Egan’s novel on the first page of the novel. The diamond lattice is the dual graph to the simplest tesselation of three dimensional space. I was working last week on two dimensional tilings, when tiling the floor of our bathroom (of course I chose hexagonal tiles, which is a 3-valent graph, the dual of a flat triangulation of the two dimensional space. The hexagonal tringular lattice is dear to me because it was somehow the start of my interest in graph theory. It must have been around 2008-2009, when I started to be interested in discrete Umlauf satz on this lattice. It eventually became this paper from 2012 which deals with a discrete Puiseux type curvature. But here finally is the start of Egan’s novel:

“In the beginning was a graph, more like diamond than graphite. Every node in this graph was tetravalent: connected by four edges to four other nodes. By a count of edges, the shortest path from any node back to itself was a loop six edges long. Every node belonged to twenty-four such loops, as well as forty-eight loops eight edges long, and four hundred and eighty that were ten edges long. The edges had no length or shape, the nodes no position; the graph consisted only of the fact that some nodes were connected to others. This pattern of connections, repeated endlessly, was all there was. In the beginning? Waking more fully, Cass corrected herself: that was the version she remembered from childhood, but these days she preferred to be more cautious. The Sarumpaet rules let you trace the history of the universe back to the vicinity of the Diamond Graph, and everything you could ask for in a Big Bang was there: low entropy, particle creation, rapidly expanding space. Whether it made sense to follow these sign-posts all the way back, though, was another question. Cass let the graph’s honeycomb pattern linger in the darkness of her skull. Having relinquished her child’s-eye view of the world, she was unable to decide which epoch of her life she actually inhabited. It was one of the minor perils of longevity: waking could be like to trying to find your way home on a street with ten thousand houses, all of which had once been your own. That the clues on the other side of her eyelids might be more enlightening was beside the point; she had to follow the internal logic of her memories back into the present before she could jolt herself awake. The Sarumpaet rules assigned a quantum amplitude to the possibility of any one graph being followed by another. Among other things, the rules predicted that if a graph contained a loop consisting of three trivalent nodes alternating with three penta-valent ones, its most likely successors would share the same pattern, but it would be shifted to an adjoining set of nodes. A loop like this was known as a photon. The rules predicted that the photon would move. (Which way? All directions were equally likely. To aim the photon took more work, superimposing a swarm of different versions that would interfere and cancel each other out when they traveled in all but one favored direction.) Other patterns could propagate in a similar fashion, and their symmetries and interactions matched up perfectly with the known fundamental particles. Every graph was still just a graph, a collection of nodes and their mutual connections, but the flaws in the diamond took on a life of their own. The current state of the universe was a long way from the Diamond Graph. Even a patch of near-vacuum in the middle of interstellar space owed its near-Euclidean geometry to the fact that it was an elaborate superposition of a multitude of graphs, each one riddled with virtual particles. And while an ideal vacuum, in all its complexity, was a known quantity, most real space departed from that ideal in an uncontrollable manner: shot through with cosmic radiation, molecular contaminants, neutrinos, and the endless faint ripple of gravitational waves.”
It has been called the hardest SciFi novel ever written. I only can confirm that I never finished the novel. Indeed, you can already be stuck in the first paragraph. I don’t remember how I got to it, maybe from the name as Schild’s ladder is an algorithm to compute geodesics in differential geometry. I had used the method when writing down and illustrating the lectures “Selected topics in the theory of calculus of variations” of Moser around 1999. I talked a bit about a discrete Schild’s ladder idea in this movie. And here are 4 slides shown during a presentation in Math 136 (Differential geometry) from Fall 2024. (Click to see it large).



Now, there is something important in the set-up of that novel in that it stresses that the works is imagined to be discrete and not just embedded in a continuum (as topological graph theorists do). Even in algebraic topology one most of the time looks at discrete structures as embedded in “real” realizations. They imagine an existing Euclidean space. It is much safer (when considering the dangers of using ZFC which we do not know and will never know to be consistent) to stay in the finite. It is not only the philosophical concerns but also that staying in the finite forces to think differently. When using geometric realizations one essentally just does numerical analysis which is usually just not nice. It is very hard to write computer code for PDE’s for example in which the difference equations actually work and are stable.
[Even in the simplest cases of one dimensional PDE’s this is tough. When I was still a grad student and Randall LeVeque had been at ETH (he gave a course on Numerical methods for conservation laws which I did not attend but where I got the book for my wife Ruth who was at that time computing numerically with PDE’s in astronomical situations like “radiative transport” and “supernovae”) and other astropphysical fluid flows. I got so interested also in PDEs ,especially integrable ones as a graduate student and worked on discrete versions like Toda systems. ]



