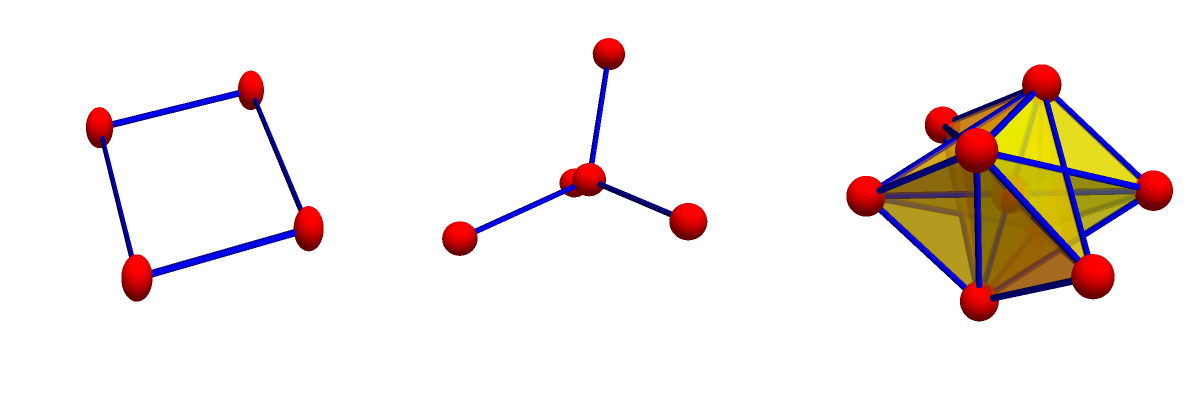
Spectra of Sums of Networks

What happens with the spectrum of the Laplacian $L$ if we add some graphs or simplicial complexes? (I owe this question to An Huang). Here is an example, where we sum a circular graph G=C₄ and a star graph H=S₄. The Laplace spectrum of G is {4,2,2,0}, the spectrum of H is {5,1,1,1,0}. The spectrum of G+H is {9, 9, 9, 7, 7, 5, 5, 5, 0}.

The largest eigenvalue

In this post just three remarks about the spectrum of sums. The first one deals with the maximal eigenvalue. In some sense, when we look at sums of graphs, we are in an extreme situation, where the maximal eigenvalue is as large as it can be. This is a bit surprising as we would expect that in general the maximal eigenvalue is smaller. But as we see, if the maximal eigenvalue is smaller, then we have an additive prime graph.

If $G=H+K$ then there is an eigenvalue $|V(H)| + |V(K)|$ of the scalar Laplacian $L$ . Consequently, any graph $G$ for which there is no eigenvalue $v_0(G)$ for $L$ is an additive prime.

Proof: If $m=|V(H)|$ and $n=|V(K)|$ , then the vector which is constant $n$ on $H$ and constant $m$ on $K$ is an eigenvector to the Laplacian $L$ with eigenvalue $n+m$ . The eigenvector is perpendicular to the constant.

Here is a corollary, which can be seen as a result in the ring of graphs as
n G is K_n . G is a multiple of a graph.

The graph $n G= G+G+ \cdots + G$ has the eigenvalue $n |V(G)|$ with multiplicity at least $n-1$ .

Proof:
The multiplicity follows because we can write the sum in $n-1$ different ways as a sum of two graphs $A+B$ . The proof above determine then the eigenvector.

The example $K_n=K_1+K_1+ \dots K_1$ , where $n$ appears with multiplicity $n-1$ is an extreme case. An other case is the $(n-1)$ -dimensional cross polytop $n P_2 = P_2 + \cdots + P_2$ which has the eigenvalue $2n$ with multiplicity $n-1$ .

I’m confident that there are more relations in general between the spectral of H.K and the spectra of H and K.

The second eigenvalue

Graphs always have the constant eigenvector to the eigenvalue 0. The first interest is the second eigenvalue which has been studied much, both in graph theory as well as differential geometry. It is somehow the ground state as we don’t want to count the zero eigenstate as something interesting. What is interesting is the first eigenvalue gap, which in the case of graphs is measured by the smallest non-zero eigenvalue $\lambda_2$ of the Laplacian.

$\lambda_2(G+H) = {\rm min}(|V(H)|,|V(K)|) + {\rm min}(\lambda_2(G),\lambda_2(H)$ .

Proof: The Courant-Fischer formula tells $\lambda_2 = {\rm inf}_{v \cdot 1 = 0} (v,Lv)/(v,v)$ . Let $v_2(H)$ be the eigenvector of $L(H)$ with eigenvalue $\lambda_2(H)$ and $v_2(G)$ the eigenvector of $L(H)$ with eigenvalue $\lambda_2(G)$ . Assume they are normalized. Extend $v_2(G)$ and $v_2(H)$ onto $G+H$ by putting $0$ on the other part. They still have norm $1$ on the product space. They are also perpendicular to the constant vector. Now $(v_2(H),L v_2(H))=\lambda_2(H)+m$ and $(v_2(G),L v_2(G)) = \lambda_2(G) + n$ . This shows $\lambda_2(G+H) \leq {\rm min}(|V(H)|,|V(K)|) + {\rm min}(\lambda_2(G),\lambda_2(H) \; .$ On the other hand, since $G+H$ can be obtained from the disjoint union of $G$ and $P_n$ (the graph without edges), by adding edges, we have $\lambda_i(G) + n \leq \lambda_i(G+H)$ . Similarly $\lambda_i(H) + m \leq \lambda_i(G+H)$ .

Here we see as an example a sequence of graphs H,H+H,H+H+H, H+H+H+H with H=P₂. These are 0,1,2,3 – dimensional spheres (cross polytopes) The eigenvalues are {0,0},{4,2,2,0},{6,6,4,4,4,0},{8,8,8,6,6,6,6,0}. Since H+H=C₄ we can also write the last 3-sphere as C₄+C₄ = K₂ . C₄ = 4 P₂.

The volume Laplacian

Here is an other spectral result. It deals with the highest form Laplacian. (See this document for some background.) Let $D=d+d^*$ be the Dirac operator of a simplicial complex. The form Laplacian $L=(d+d^*)^2$ splits into blocks called form Laplacians $L_k$ . The nullity of $L_k$ is the $k$ ‘th Betti number $b_k$ see. We have already seen that if we have two graphs $G,H$ , then the volume of $G+H$ is the product of the volumes of $G$ and volumes of $H$ . Lets write $L_v(G)$ for $L_{{\rm dim}(G)}(G)$ for the volume Laplacian, the Laplacian belonging to the largest dimension. Now if $G$ has volume $m$ and $H$ has volume $n$ then we can look at the volume eigenvalues $\lambda_1, \dots, \lambda_n$ of $L_v(G)$ and the volume eigenvalues $\mu_1, \dots , \mu_m$ of $L_v(H)$ . What are the volume eigenvalues of $H+G$ ?

For two arbitrary networks, the volume eigenvalues of $H+G$ are given by $\lambda+\mu$ , where $\lambda$ runs over the volume eigenvalues of $H$ and $\mu$ runs over the volume eigenvalues of $G$ .

Proof: If $U$ is the volume Laplacian of $G$ and $K$ is the volume Laplacian of $H$ . Given $U v = \lambda v$ and $V w = \mu w$ . The volume Laplacian $W$ of $G+H$ is a $(nm) \times (nm)$ matrix as the volumes of $G$ and $K$ have multiplied. Define on the facet $xy$ of $G+H$ joining the facets $x$ and $y$ of $G$ and $H$ the value $f_{xy} = v_x w_y$ . Now $W f = \lambda f + \mu f$ .

The largest eigenvalue

The second eigenvalue

The volume Laplacian

Author: oliverknill

Leave a Reply Cancel reply