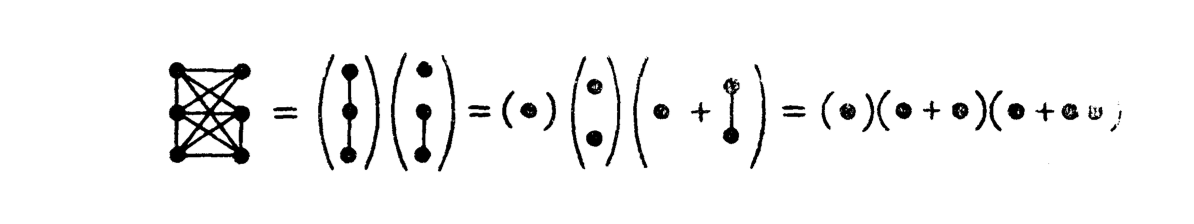A ring of networks

We explore here a ring of networks which naturally extends the ring of integers. It might allow to use of commutative algebra to be used in graph theory. Since algebraic geometry notions have naturally been extended to commutative rings, one gets now a huge playground to investigate. What is the number theory of primes, how hard is prime factorization, what is the spectrum in that ring? What are the topological properties of the spectrum etc. But at first it is much more primitive. We can explore a “number system” similarly as the first mathematicians explored the number system of integers or in parallel, what kids explore when learning numbers. What are the negative numbers, what are fractions, what are the prime numbers? Is there a natural field containing this ring? Can this field be completed so that one can do analysis on it (the real and complex numbers)? Can one do cryptology with this ring? But like a kid exploring numbers, we can explore here a number system which has not been considered yet. It is a proud result of fraction lab.

In an older post, the problem of unique prime factorization in the monoid (finite simple graphs, join *) has been raised. After having tried in vain for two weeks to find an addition which is both natural and renders the networks into a ring and * the multiplication (this is suggested by the fact that the join is very much related to the Cartesian product and because it can be implemented nicely algebraically as a multiplication in a Stanley-Reisner ring), it appears better to let the join be the addition in a ring. The Grothendieck construction (which parallels the Egyptian invention of fractions) renders the monoid into an Abelian group. But what is the multiplication? I think to have found one. Since K_n * K_m = K _n+m why not look at a multiplication which has the property that K_n x K_m = K _{n m} and which satisfies the distributive property Gx(A*B) = GxA * GxB. There is such an operation. As the number of vertices now should multiply. After checking through a few candidates of multiplications and and checking the distributivity property on random graphs, a multiplication in which the vertex set is the Cartesian product appeared.

So, I will write here the join operation with a plus sign +. Remember, the join of two graphs takes the disjoint union of the vertex sets, leave the old connections and then connect any pair belonging to different graphs. We will look at the problem to get a natural representation of the negative graphs later. The 0 element is the empty graph. The monoid (graphs, +, 0) has still an interesting prime factorization problem. Graphs play the role of integers and an additive prime is a graph G which can not be written as H+K, with two non-zero graphs. In integer arithmetic, we have only one additive prime, it is 1. All other integers can be factored like 5=1+1+1+1+1. The additive prime factorization problem is trivial in numbers. We have seen it to be interesting for networks.

What is the product x? Once we explore this with experiments, starting with the fact that 2xG = G+G, etc, it is actually straight forward:

Just take as vertex set the Cartesian product of the vertex sets of the two graphs, the connect any two pairs, if one or both of the projections onto the first or second graph is an edge.

I don’t know whether this product corresponds to any topological construction in the continuum (the tensor product comes close in the case of linear spaces). It would be a product of topological spaces in which the quantity c(G) = (dimension(G)+1) is multiplicative. This product has nice properties. It has the one-point-graph K₁ as one element 1, the multiplication is commutative and distributive. It extends the usual arithmetic of integers. How do we think about negative numbers like -3? It is the complete graph with three vertices coming with a negative sign. Let X be the smallest set of objects generated by complete graphs which is closed under both addition and multiplication. This object X now plays the role of the ring of integers.

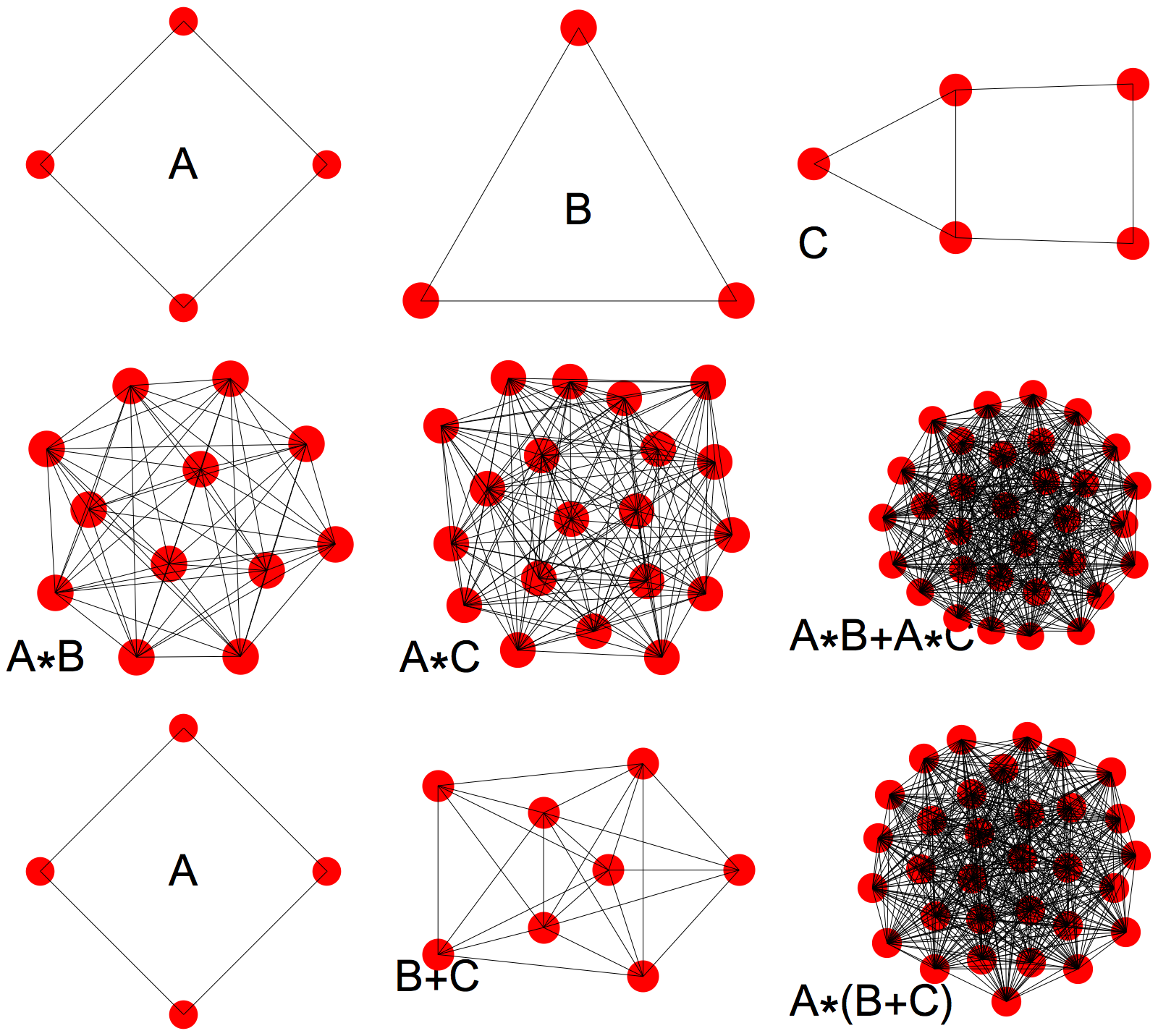
The algebraic structure (X, +,0,x,1) is a commutative ring. It contains the bi-monoid (graphs,+,0,x,1) of graphs. It contains the sub ring of all complete graphs (together with negative complete graphs) which is isomorphic to the usual ring of integers (Z,+,0,x,1). On that subring, the ring isomorphism is given by the clique number c(G)=dim(G)+1 as c(Kn) = n and c(Kn + Km) = n+m and c(Kn x Km) = n m.

Proof. We have to check the axioms of a ring. Both the addition and multiplication are associative and commutative. For the associativity of the multiplication we note that GxHxK is the graph for which the vertices are the cartesian product of the vertex sets of the individual factors and where two triples are connected, if at least one of the projections is connected. The neutral elements zero as the empty graph and one as the one-point graph are clear. The existence of an inverse is by construction (even so with little intuition about negative graphs so far). The distributivity is the only thing which really needs to be checked. Like in the case of the ring of integers, spacial geometric insight can help by placing the graphs H,K and H+K into one coordinate axes and G onto the other. Now both GxH + GxK and Gx(H+K) have as the vertex set the product sets of the vertices. As connections in a sum H+K consist of three types, connections within H, connections within K and any possible connection between H and K, two points (a,b), (c,d) are connected if either (a,c) is an edge in H, or (b,d) is an edge in K
or then if either a,c or b,d are in different graphs. We can also partition GxH + GxK into three sets, connections ((a,b),(c,d)) within GxH
or connections ((a,b),(c,d)) within GxK or then connections between any pairs ((a,b),(c,d)) for which (a,b) and (c,d) belong to different graphs GxH or GxK.

So, here we see the addition and multiplication of complete graphs:

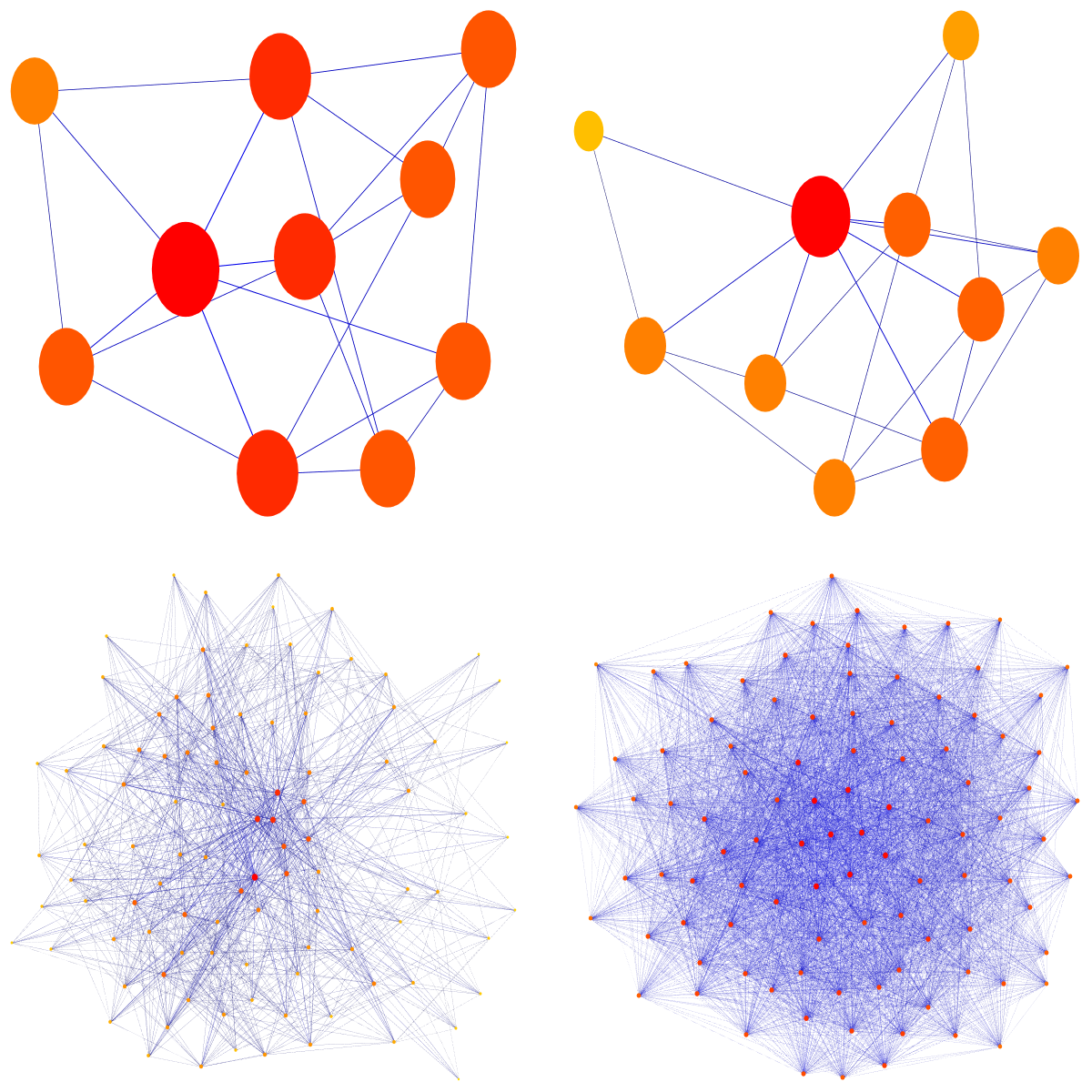
Here we see the addition and multiplication of two random graphs:

All the questions about prime factorization etc can be asked before. The existence of primes and prime factorization (Euclid’s lemma) is straightforward

There are infinitely many multiplicative primes. Every graph with a prime number of vertices is prime. There is a prime factorization.

The question about 3unique prime factorization is also still open. So, we have now two unique prime factorization problems. One for addition and one for multiplication.

The arithmetic of networks is more interesting. In any case, we don’t even have scratched the surface even for “school arithmetic” since we want to represent general elements in the graph nicely. The Grothendieck representation as an equivalence class of pairs definitely does not cut it but we might have to represent elements as pairs of graphs. Is there a way to do it with one graph, possibly by putting some positive and negative marks? Is there a way to see when such a representation is reduced? This is similar to see whether a fraction 35/14 is reduced or not. How do we spot multiplicative factors which can be factored out? While we consider that problem trivial for integers, it is already not: is 23536481273/445751025857 reduced? We already need a computer to answer this as there is a prime factor 104729. We know the integer factorization problem is hard in integers and having the ring of integers contained in the ring of networks, we definitely also know:

The network factorization problem in the ring of networks is at least as hard as the integer factorization problem.

It could be much harder although as we need also to figure out the connection parts in the factors. The brutal brute force attack is to factor the vertex cardinality then write the vertex set as a Cartesian product of two sets with that cardinality, then figure out the connections.
Here is a product graph P*Q with p*q = 5*7 vertices. The network P has 5 vertices, network Q has 7 vertices. The product PxQ has 35 vertices. Can we find the factors easily?

Here are the factors. The first one is the rabbit graph, the second, the mouse graph

One could try whether values of some functionals allow to get insight into the factorization. But so far, none has been found. The Euler characteristic of the factors are 1,0. The Euler characteristic of the product is 12 in this case. The vertex degrees are (2, 4, 1, 1, 2) and (4, 3, 2,2,3,3,3). The product has the vertex degrees (26, 23, 20, 20, 23, 23, 23, 26, 23, 20, 20, 23, 23, 23, 32, 31, 30, 30, 31, 31, 31, 23, 19, 15, 15, 19, 19, 19, 23, 19, 15, 15, 19, 19, 19). But there would be a lot more to look at, like the topology of unit spheres, curvatures etc.

It looks as if also an other enigma, the problem to find a modular arithmetic in networks can be reasonable, as we have a ring. We can take a multiplicative prime like P= K₃ and look at all networks modulo this prime. In other words, two networks G,H are the same modulo P, if G = H + KxP for some other network K. In order to have this to work, we need the Euclidean algorithm to work which asks for the ring to be an Euclidean domain.

This is not obvious at all or could be false. The Euclidean function one can shoot for the clique number or number of vertices of a graph. The question is now that if G is a ring element and P is given, can we find K such that the clique number of G-K*P is smaller than the clique number of P. Can this K be made unique by minimizing the clique number or maybe even by minimizing the number of vertices.
But first we need to play more with the arithmetic.

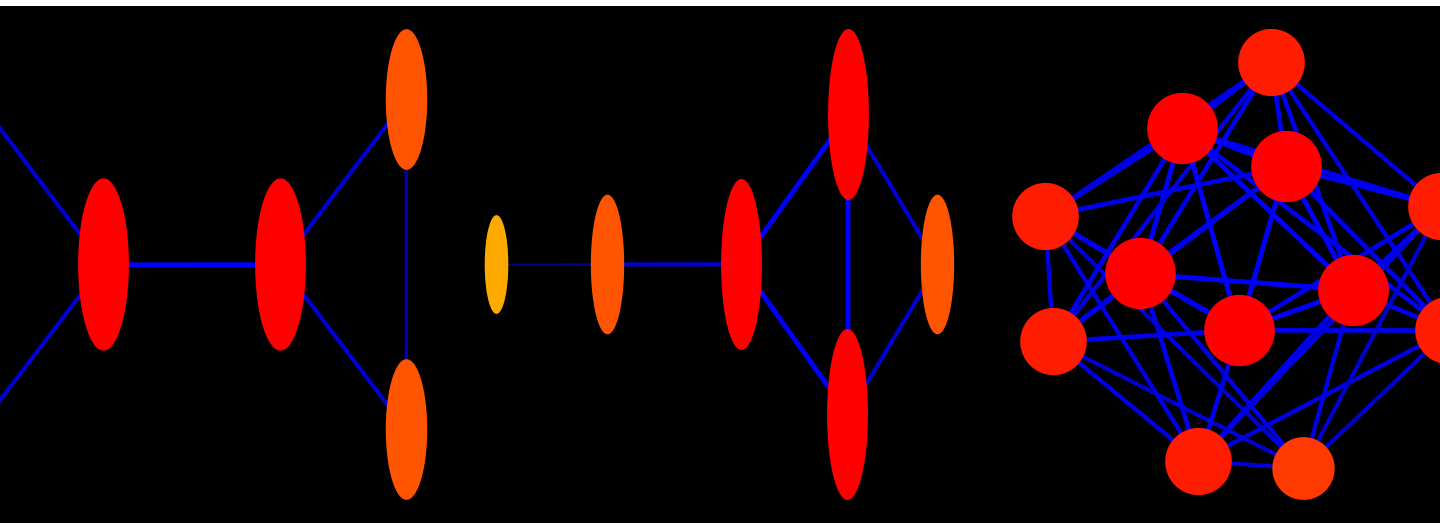
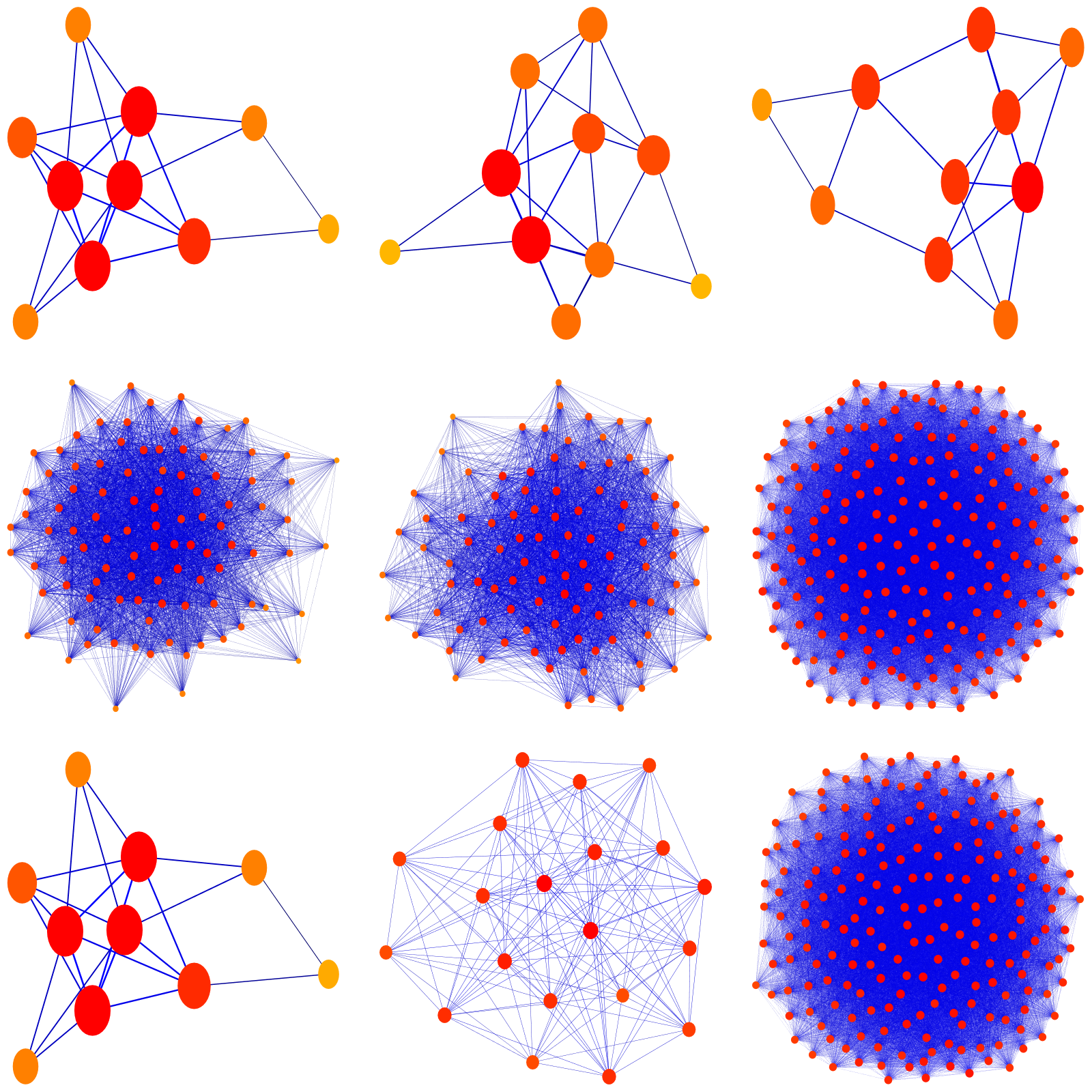
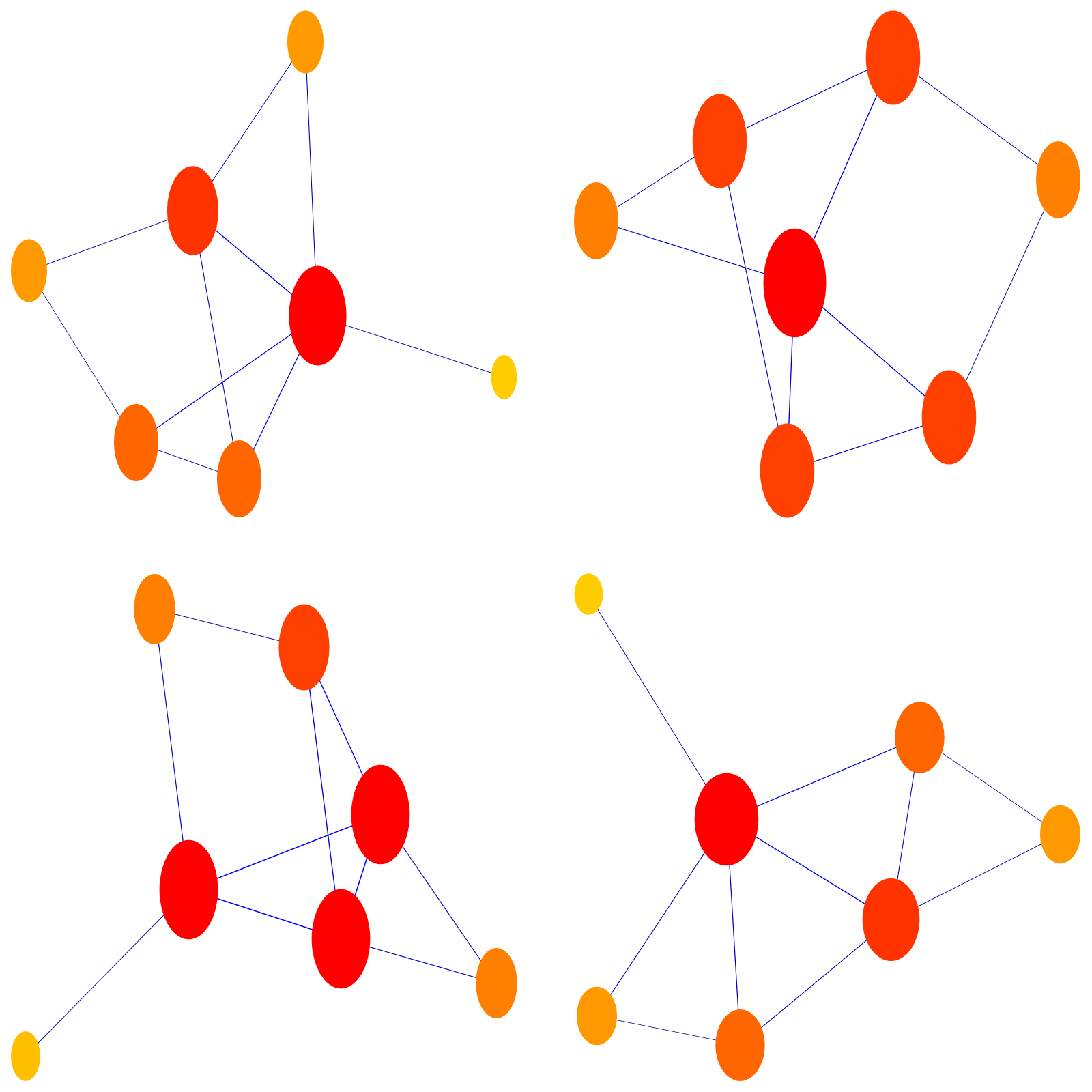
Here is an illustration of the distributivity law G x (H+K) = G x H + G x K: we take 3 random graphs G,H,K (and display them in the first row). In the second row, we see the graphs G x H, G x K and G x H + G x K. In the third row, we see G and (H+K), and then G x (H + K). You notice that the two graphs G x (H+K) and GxH + G x K look different as they were constructed differently. But they are isomorphic (as we can check in Mathematica with IsomorphicGraphQ):

[By the way, the tensor product of graphs mentioned earlier when comparing different products is different from the just described product. Thats why it is probably not a good idea to call it tensor product. I call it just the “product in the ring of networks”. Here is a picture which shows the comparison between the standard tensor product of graphs and the new product x we have introduced here: we take two random graphs. To the left below we see the tensor product, to the right the ring product. You can readily check with examples that the tensor product does not play well together with the join. Distributivity fails! We have distributivity however for the new product.

]

An observation about symmetry:

If A is the automorphism group of the graph G and B is the automorphism group of the graph H, then the automorphism group of G x H contains the product group A x B.

An obvious question is whether the automorphism group can be larger. It definitely can, like if G=H, then there is also an involution switching the two networks.

Here are some examples of arithmetic. We write for the graph with n vertices and no edge, the cyclic graph with $n$ vertices, the wheel graph (n spikes) with n+1 vertices and the star graph with vertices (n rays). First some things we have already mentioned.

a) b) c) d) cone over G e) wheel graph f) suspension g) octahedron graph Oct h) utility graph i) complete bipartite graph j) star graph k) windmill graph

We see so that for a cone graph G, the graph G-1 is again a graph. There is no graph representing -1. The reason is that the cone over such a graph would be a non-empty graph but -1 + 1 = 0. Here some identities which first surprise:

A) three sphere B) is an 7-dimensional sphere

However, it becomes clear if we write . More generally, we see

If $G$ is a n-dimensional sphere, then the product is a ((n+1) m-1)-dimensional sphere. Linear combinations of spheres with integer a,b are spheres.

When computing in the field of rational networks, we need to represent the elements as (A-B)/(C-D). For example, the number -3/7 is represented by (-K₃|0)/(0|K₇). But there are of course much more general elements (A-B)/(C-D) like:

One of the challenges will be to be able to reduce such an expression. A silly example is (C₄ | O)/(K₅|K₃) which simplifies to P₂/K₂. A completely open question for me is to complete the field, that is to find a metric or valuation which allows to take such limits then take equivalence classes of Cauchy sequences. Like in the case of extending the rational number to the reals, it is important to have that since we want to define things like exp(G) or zeta(s) defined by the primes in the ring.

[ January 29: One can suspect that the arithmetic of networks has to do with the arithmetic of Surreal numbers but the later is totally ordered. Also, the addition and multiplication looks different. For the extension of “games”, there is more chance as Games only form a partial order and there could be some overlap. I don’t see any resemblance however yet. ]

Here is a graphical illustration of the computation 1/3 + 1/2=5/6

And here is a computation with some other “network numbers”, which are fractions but do no more correspond to rational fractions:

Just seeing how complicated even small products can become, it becomes unlikely that even computations involving factors of a few dozen entries
can be done reasonably by hand. Maybe that is just what can make the ring attractive for cryptology. However, for being useful as such, one would need a modular arithmetic in the ring of networks so that one can deal with a finite group, similarly as with arithmetic on elliptic curves over some prime.

A concrete question is to find G mod K₂, as K₂ is one of the smallest multiplicative prime graphs in the ring of integers,
or G modulo the prime P₂, which is the zero dimensional sphere and even smaller than K₂? While the graph K₂ x G is equal to G + G, the join of G with itself, the graph P₂ x G consists of just two copies of G without any connections between the two parts. But what does it mean to take a graph modulo P₂? They are equivalence classes where two A,B are equivalent, if A=B+G x P₂ for some G. It is questionable whether there are finitely many equivalence classes. An other thing to explore is whether to fix a host graph G and both when adding or multiplying networks reuse old vertices. This would seriously change the arithmetic. The elements of the finite group would be the sub graphs of G but already addition is questionable. One could try the symmetric difference of vertices but what about the connections? Just deleting the connections to the intersections? And then the multiplication. On the ring of sets, the intersection is the multiplication. But this has little to do with the multiplication defined above. Even if we wanted to extend the Boolean ring on the vertex set to networks, this does not work. Graphs form only a Boolean lattice, not a Boolean ring. It appears that a modular arithmetic based on a host graph is not obvious. Especially if we want to have it relate to the entire ring of networks.

[Added May 17, 2017: finally could get hold of the Zykov article. Here is a picture from that article:

Obviously, the addition is the disjoint union and the multiplication what we here use as the Zykov addition. But the addition and multiplication are not compatible as (A+B)*C = A*C + B*C would imply with that interpretation that we have on the right hand side something disconnected and on the left hand side a connected graph. Any way, here is an other picture illustrating that with the Zykov addition and our new multiplication, we have distributivity:

In our case, the cardinalities of the graphs follow the usual arithmetic.
End addition].