Over the weekend, I gave a glimpse on some code which allows to compute the cohomology of an open or closed set in a simplicial complex. Here are 5 lines for cohomology. We see how elegant this can all be. Simplicity, Clarity and Generality. This code could in principle compute the cohomology of any simplicial complex. Of course, the machine has to be able to handle the matrices.

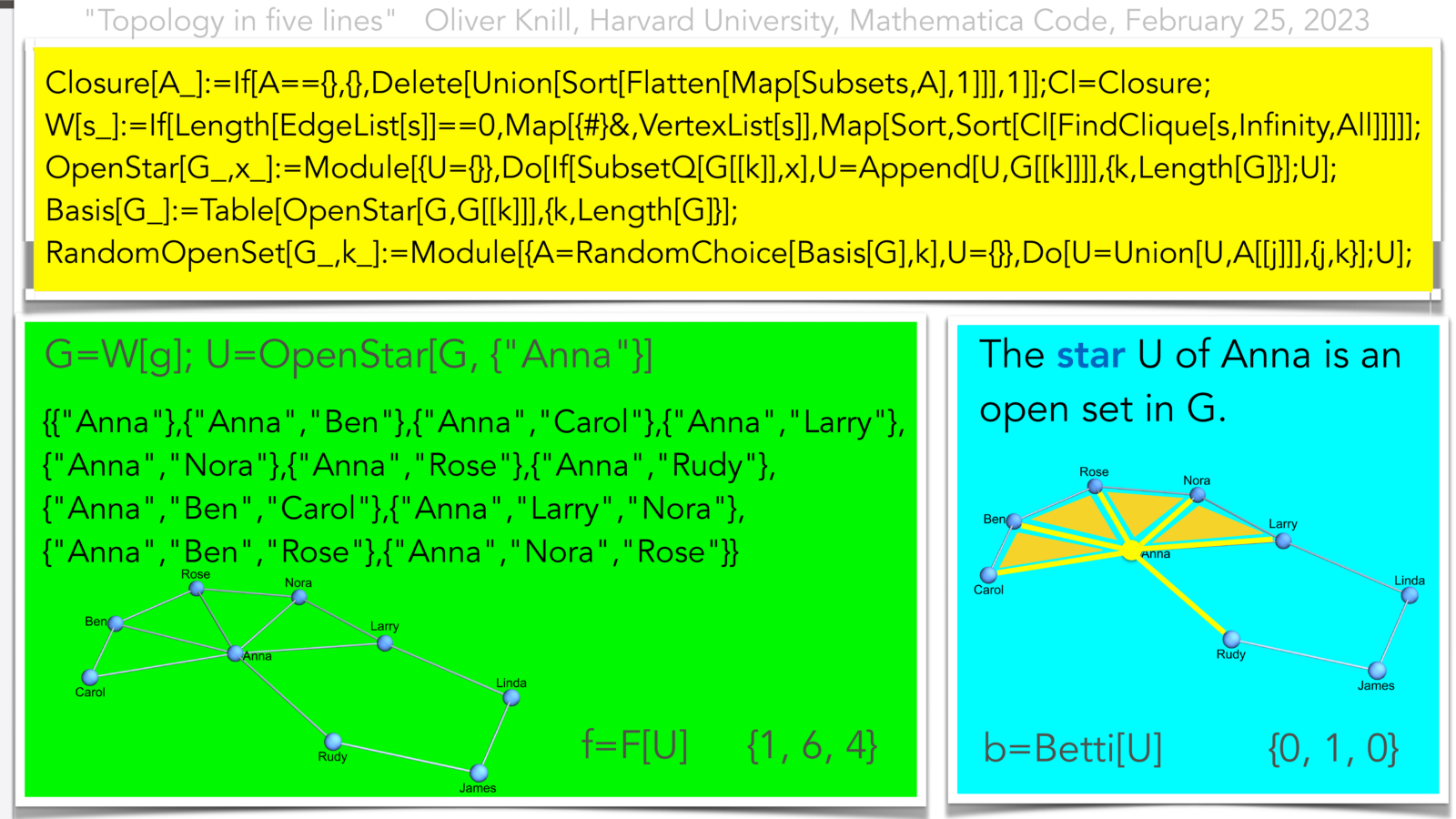
And here are 5 lines allowing to compute a random open set in a simplicial complex. As an example, I take the friendship graph complex, a finite abstract simplicial complex with 11 elements. The cohomology is given by the Betti vector (1,1,0) which is clear also because the complex is homotopic to a circle. The star of Anna has cohomology b(U) = (0,1,0). There is one connectivity component and one loop. The unit sphere S of Anna is the union of a line graph and single point {Rudy}. Its Betti vector is b(S) = (2,0,0). The Unit ball B of Anna, a simplicial complex again is contractible with Betti vector u(B) = (1,0,0). The fusion rule is (b(U) + b(S) = b(B) + b(I), where b(I) = (1,1,0) is the interaction cohomology.
(* Show me the code presentation of February 26, 2023, Oliver Knill *)
(* 5 lines for Cohomology, Oliver Knill, Harvard University, Mathematica Code February 24, 2023 *)
F[G_]:=Module[{l=Map[Length,G]},If[G=={},{},Table[Sum[If[l[[j]]==k,1,0],{j,Length[l]}],{k,Max[l]}]]];
s[x_]:=Signature[x];L=Length;s[x_,y_]:=If[SubsetQ[x,y]&&(L[x]==L[y]+1),s[Prepend[y,Complement[x,y][[1]]]]*s[x],0];
Dirac[G_]:=Module[{f=F[G],b,d,n=Length[G]},b=Prepend[Table[Sum[f[[l]],{l,k}],{k,Length[f]}],0];
d=Table[s[G[[i]],G[[j]]],{i,n},{j,n}]; {d+Transpose[d],b}];
Hodge[G_]:=Module[{Q,b,H},{Q,b}=Dirac[G];H=Q.Q;Table[Table[H[[b[[k]]+i,b[[k]]+j]],{i,b[[k+1]]-b[[k]]},
{j,b[[k+1]]-b[[k]]}],{k,Length[b]-1}]]; nu[A_]:=If[A=={},0,Length[NullSpace[A]]];Betti[G_]:=Map[nu,Hodge[G]];
(* 5 lines for Topology, Oliver Knill, Harvard University, Mathematica Code February 24, 2023 *)
Closure[A_]:=If[A=={},{},Delete[Union[Sort[Flatten[Map[Subsets,A],1]]],1]];Cl=Closure;
W[s_]:=If[Length[EdgeList[s]]==0,Map[{#}&,VertexList[s]],Map[Sort,Sort[Cl[FindClique[s,Infinity,All]]]]];
OpenStar[G_,x_]:=Module[{U={}},Do[If[SubsetQ[G[[k]],x],U=Append[U,G[[k]]]],{k,Length[G]}];U];
Basis[G_]:=Table[OpenStar[G,G[[k]]],{k,Length[G]}]; Stars=Basis; EulerChi[A_]:=Total[Map[w,A]];
RandomOpenSet[G_,k_]:=Module[{A=RandomChoice[Basis[G],k],U={}},Do[U=Union[U,A[[j]]],{j,k}];U];
(* first slide for https://www.youtube.com/watch?v=GRzqwghVqYg *)
g=ExampleData[{"NetworkGraph","Friendship"}]; G=W[g];
f=F[G]
b=Betti[G]
Q=First[Dirac[G]]; MatrixPlot[Q]
H=Q.Q; MatrixPlot[H]
(* second slide https://www.youtube.com/watch?v=GRzqwghVqYg *)
U=OpenStar[G,{"Anna"}]; f=F[U]
B=Closure[U]; S=Complement[B,U];
{bU,bS,bB}=PadRight[{Betti[U],Betti[S],Betti[B]}]; bI=bU+bS-bB;
{bU,bS,bB,bI}

