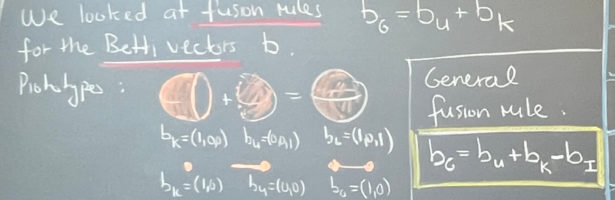Over the winter break I started to look at Mayer-Vietoris type rules when looking at cohomology of subsets of a simplicial complex. See January 28, 2023 (Youtube) , and February 4th 2023 (Youtube) and most recently on February 19, 2023 (Youtube). Classically, cohomology is considered for simplicial complexes and especially for closed sets. If a cohomology is considered for open sets, then this is classically done by exhaustion. We do something different. The cohomology of an open set in the simplicial complex
for example has Betti vector
matching that the super sum of it is the Euler characteristic -1 of U. When fusing this open set with a closed interval like G, we get a circle with Betti vector (1,1). The cohomology adds simply up like Euler characteristic. In a combinatorial frame work, one has much more freedom and one can ask for the cohomology of an arbitrary set of sets (sometimes called multi-graph). But that is too large. For arbitrary set of sets, cohomology simply does not work in general. If G is an arbitrary set of sets one has the Euler characteristic
, where
, but there is no reasonable non-trivial exterior derivative satisfying
in general. It was a bit of a surprise for us that there is a cohomology for open sets U in a simplicial complex G and even a bit more surprising that nobody seems have looked at it before. But finite topological spaces are usually only considered in enumerative combinatorics, a subject which has separated even within combinatorics in the 1960ies to become its own field. In quantum calculus frame works of course, finite topologies are the bread and butter. We do not believe here in the continuum. We do not believe here in infinity.
I talked a lot about finite topology on simplicial complexes G recently. It is something which is extremely interesting because there has very little in common with the topology of geometric realizations. The topology is generated by stars in the complex and is not Hausdorff for example. But the cohomology for these open sets works beautifully. Open sets are more “free” because we can realize any Betti vector and similarly also realize any f-vector (this is not possible for closed set and the theorem of Kruskal-Katona gives the answer which are possible). As we are in a strictly finite frame work, there is no “limit” involved anywhere. The usual definition of the exterior derivative works, the computation of the cohomology is just the computation of the nullity of the matrices (Hodge blocks) as in the case of closed sets. As reported in the videos and mentioned in my seed paper (ArXiv), there are quite a bit of surprises (the biggest of course is that very few attention has historically been given to finite topologies. There is an interesting episode between Hausdorff, the main father of set theoretical topology and Alexandroff. Hausdorff felt that metric spaces are good enough and focused on those maybe also for pedagogical reasons. Alexandroff would have preferred the more general set-up. But non-metric spaces are so much richer and also appear naturally when looking at simplicial complexes). One also sees often that the Betti vector b(K) of a closed set K and the Betti vector b(U) of its complement adds up to the Betti vector of b(G). But is is not always the sum. There is an interface cohomology. To see that this the case, I checked first experimentally that
is always a non-negative vector if G is an arbitrary simplicial complex and
is an open-closed pair in the complex. This is not obvious and needs to be proven. I call it the remaining Betti vector the interface cohomology because it is the cohomology of the interaction between the open and closed set (even so they have no common intersection, they interact as the derivative reaches out from one set to the other).

Screen shot from the youtube movie from February 19th 2023, where I’m already sure that the interface cohomology Betti vector b(I) is non-negative. In many manifold cases, the interface cohomology turned out to be trivial. An example is if we glue orientable manifolds with connected sum constructions along spheres. There is already a non-trivial interface cohomology when gluing an open disk to a closed Moebius strip. In that case , b(I)=(0,1,1). There is a harmonic 2 form on the open disk but this does not survive the transition to the projective plane as this is a manifold which is not orientable and so does not carry a volume form. In the prototype example, where we glue a closed disk to an open disk, things work (1,0,0) + (0,0,1) = (1,0,1) gives the cohomology of the 2-sphere.
I made now much more experiments and I’m sure that there is a general fusion formula true for all simplicial complexes G and all open subsets U om G with complement K in the complex. Again, this is not obvious. In principle, the remaining cohomology vector b(I) could become negative. Of course, Euler-Poincare holds for the cohomology of closed sets (as Poincare already knew). It also holds for open sets (one can see this very elegantly using McKean Singer which of course works in any elementary cohomology frame work where one has a Dirac operator
). From Euler-Poincare and the fact that the Euler characteristic of U and K add to the Euler characteristic of G (because K,U are the disjoint union in G filling out G) one has that the super sum of
must be zero. It represents the empty set sitting between U and K. But this interface is not inactive. It produces an “interaction between cohomology classes of U and H which fuse to cohomologies in G. In the process, collision particles are obtained. I really like to think about these things like a physics person. Harmonic forms are some sort of “particles”.
Already in my January 28, 2023 (Youtube) , I mentioned that the fusion should be “easy to prove” using the heat flow. (P.S. It might be difficult of course, but it is always good to assume at first that a problem is easy. At the moment I do not know how hard things really are.) Indeed, the heat flow is not only intuitive , it is also a practical way to generate cohomology classes: start with an arbitrary function on the simplicial complex G and apply the heat flow , where
is the Hodge Laplacian. We end up with a cohomology class. In order to show that b(I) is non-negative, one has to verify that every cohomology class f in G can be obtained from merging a cohomology class g on U and a cohomology class h on K. Practically this means that we can find g and h such that the heat flow applied to g+H leads to the harmonic f. I call this fusing but it is something which appears in Mayer-Vietoris. Here it is very natural. Take a harmonic function on U and a harmonic function on K (both represent of course cohomology classes in their cohomologies). This defines now a function on G simply because U and K are just complements in a finite set. Now apply the heat flow. This produces a cohomology class on G. What happens is (of course this needs to be proven) that we can reach like that any cohomology in G. This is usually expressed in fancy words like “short exact sequence” but it is simply that the dimension of the image is the dimension of the kernel of L_G, the Laplacian on G. The key is to reach every cohomology class because now we have just a linear map from
to
. The kernel of this map is
. That the dimension of the kernel and the dimension of the image add up is the rank-nullity theorem (which we just taught last week in linear algebra).
So far things look good. The statement that has been confirmed to be true in all cases considered (I take a random simplicial complex a random open set and check). I also applied the heat flow to fuse cohomology classes
and computed the rank of this projection map onto H(G) obtained by applying the heat flow on the fused function. This linear map is surjective in the cases checked. This then allows to conclude that
with vectors which are all non-negative. This is just the vector form of the rank-nulity theorem. Note that restricting the projection or heat flow onto k-forms produces a flow on k-forms, but again, it is so much easier to avoid the language of chain complexes and use the Dirac and Hodge frame work as it brings the hole story into something which can be taught in a first semester linear algebra courses. At the moment, I do not expect it to be difficult to show that that the heat flow from the fused harmonic forms on U and K reaches all the harmonic forms on G. But as for now, I do not have the proof yet. It would be super if given a harmonic f, we could just write down a harmonic g of U and a harmonic h of K such that the heat flow applied to g+h produces f.
In the presentation last Saturday, I did not have much to say about this yet. So, I added a bit of Q and A about “Nothing” with Chat GPT. The concept of empty set is actually very important here. When looking at open sets, then we naturally do not have all vector spaces of k-forms filled. These vector spaces can be trivial and the Hodge block is the 0x0 matrix. I also ranted a bit about the confusion one has in the math literature about the empty set. Considering the empty set a simplex is not a good idea. The empty set is a simplical complex itself, the (-1) dimensional sphere. A simplicial complex should not contain the empty set. There are frame works which include the empty set (and especially in Matroid theory one has always the empty set included) but that needs also adaptations which are simply awkward when looking at the situation with the eyes of a topologist.