This is a bit of an update on the problem to find the limiting law in the Barycentric central limit theorem. (See some older slides.) The distribution has first experimentally been found in the PeKeNePaPeTe paper in 2012. I proved universality in 2015 using a modification of the Lidski theorem by Last.
That general theorem tells that the difference between the eigenvalue sequence of two symmetric matrices is bounded above by the
difference of the matrices:
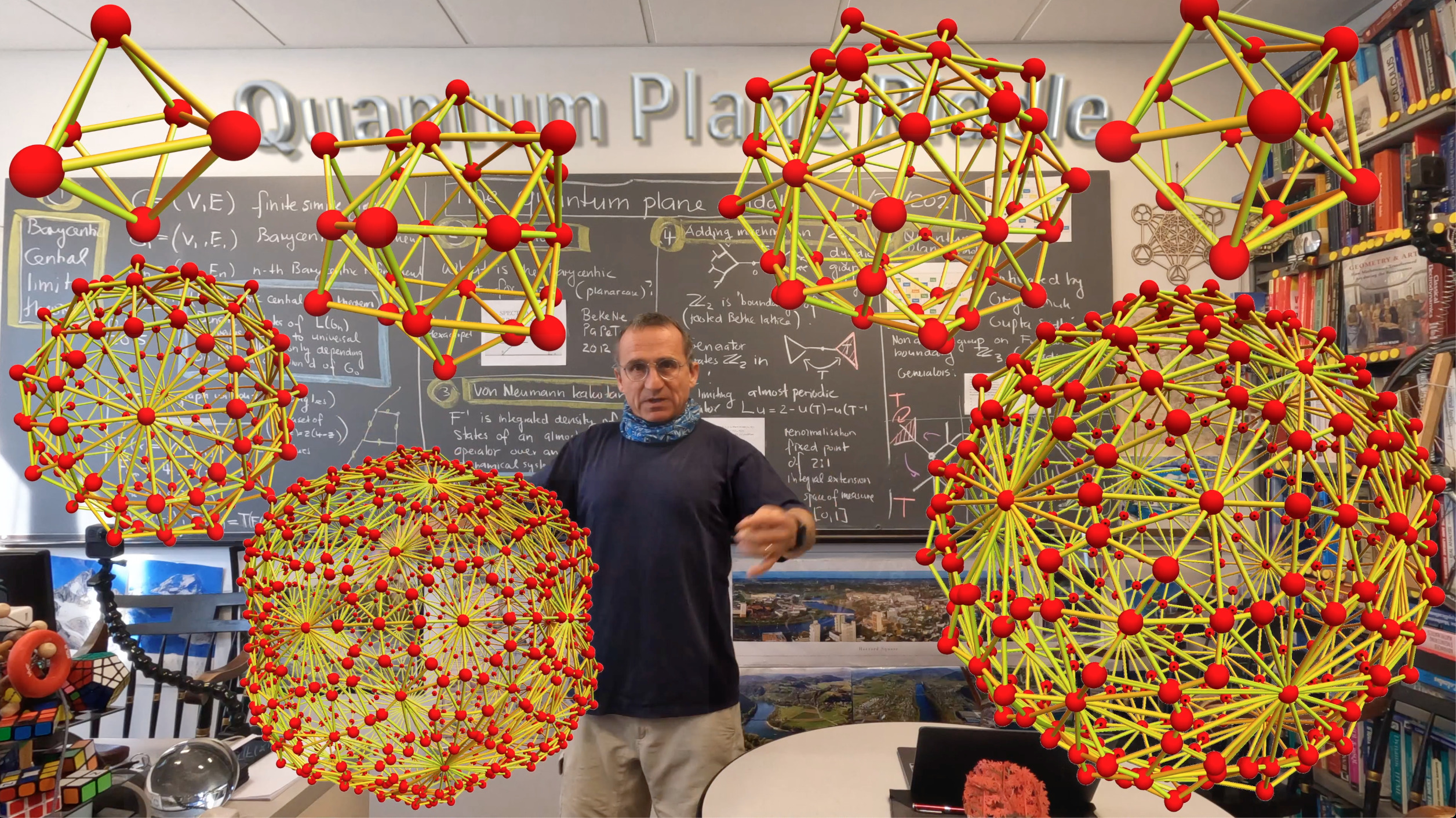
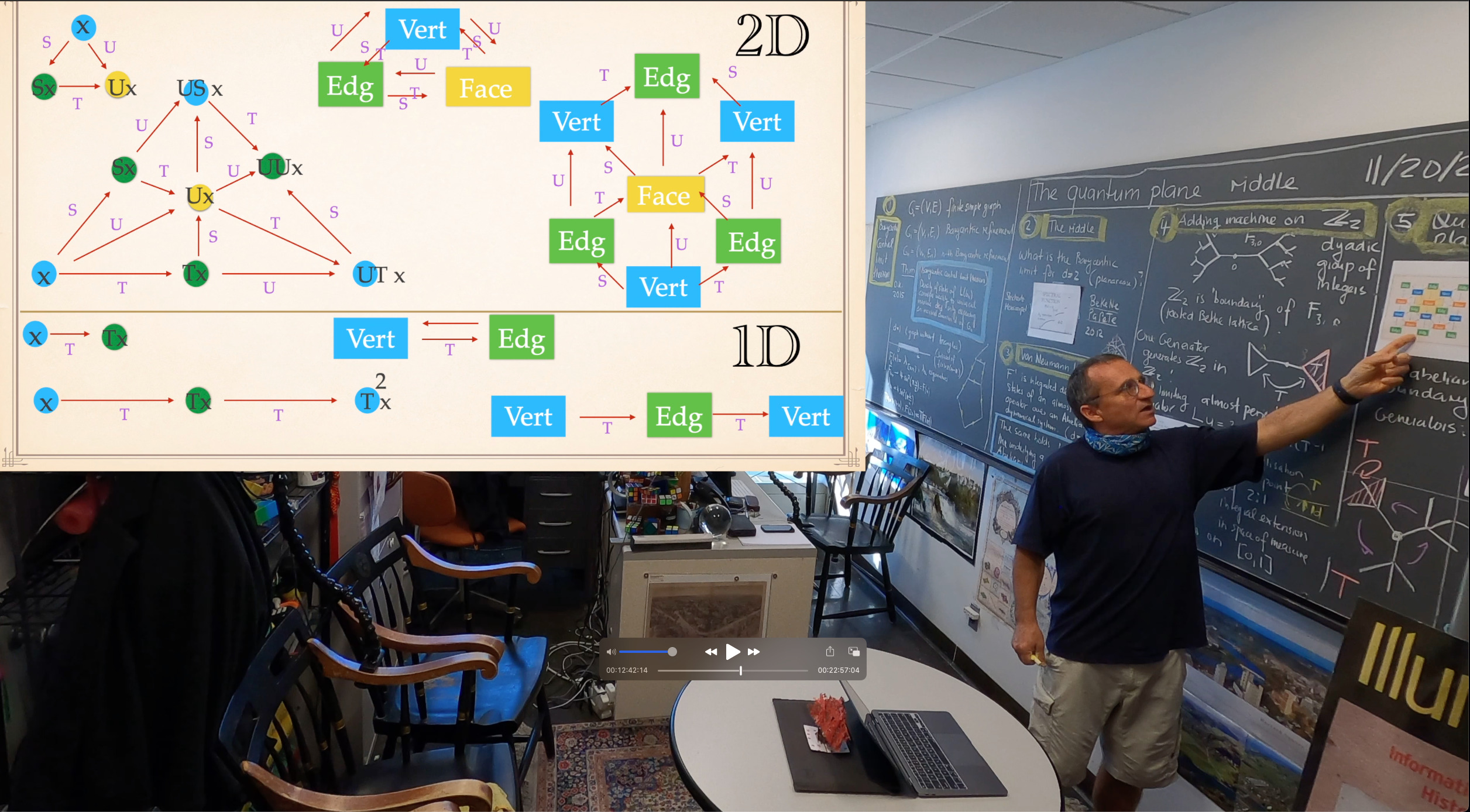
. This inequality in a graph theoretical setting immediately implies that the sum of the absolute values of the eigenvalue differences of Kirchhoff Laplacians of two different subgraphs of a complete graph is the smaller or equal than the minimal number of edges which need to be modified to get from one graph to the other. What makes the theorem tick is that under Barycentric subdivision, lower dimensional parts grow exponentially slower than the highest dimensional parts. This means that essentially, a Barycentric subdivision behaves like a self-similar graph. Having talked just last week a bit about the exciting Grigorchuk and Gupta-Sidki groups and already speculated in 2015 that there should be a self-similar almost periodic operator in the limit having the density of states as the central limit law, I thought to recall this “quantum plane riddle”. The problem is to understand the following picture.

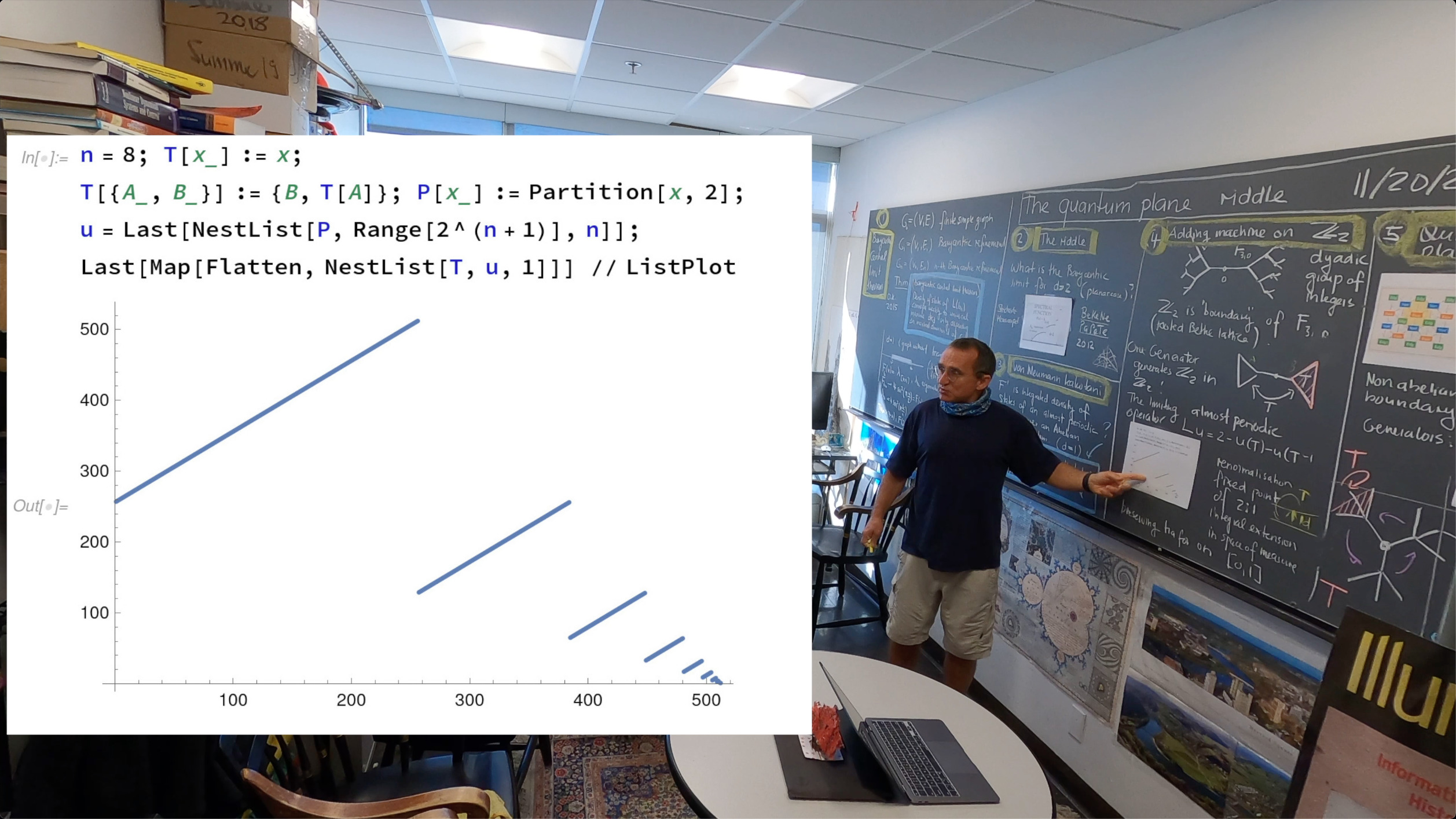
The code for plotting the graph to the left is seen here in the Wolfram community pages. The quantum plane riddle is the problem to understand the nature of this picture. Prove that there are gaps. Identify the operator which produces this picture.The picture is universal: start with a graph having no sub graph, then the eigenvalues of the Kirchhoff Laplacian after a few Barycentric refinements look as such.