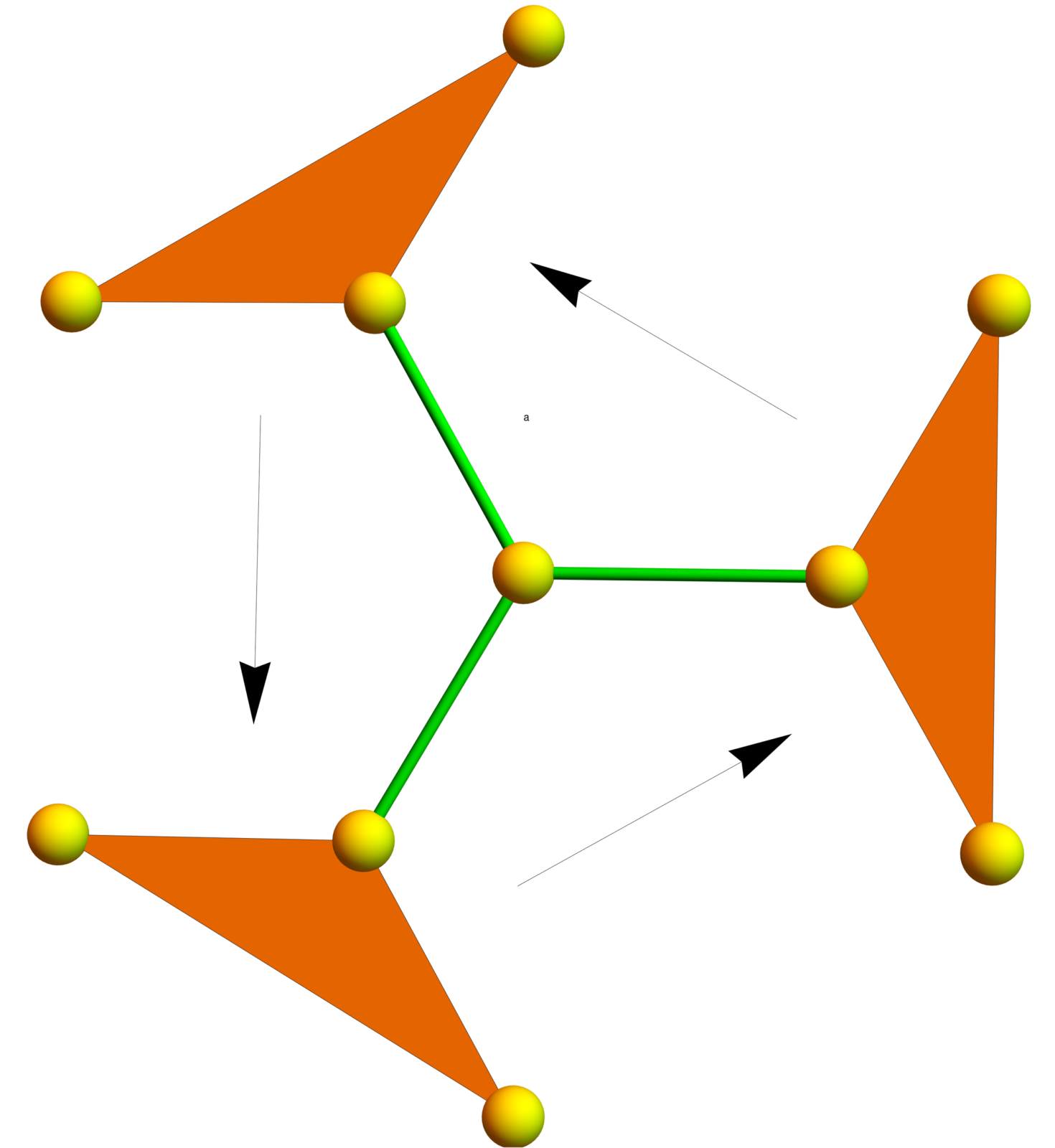
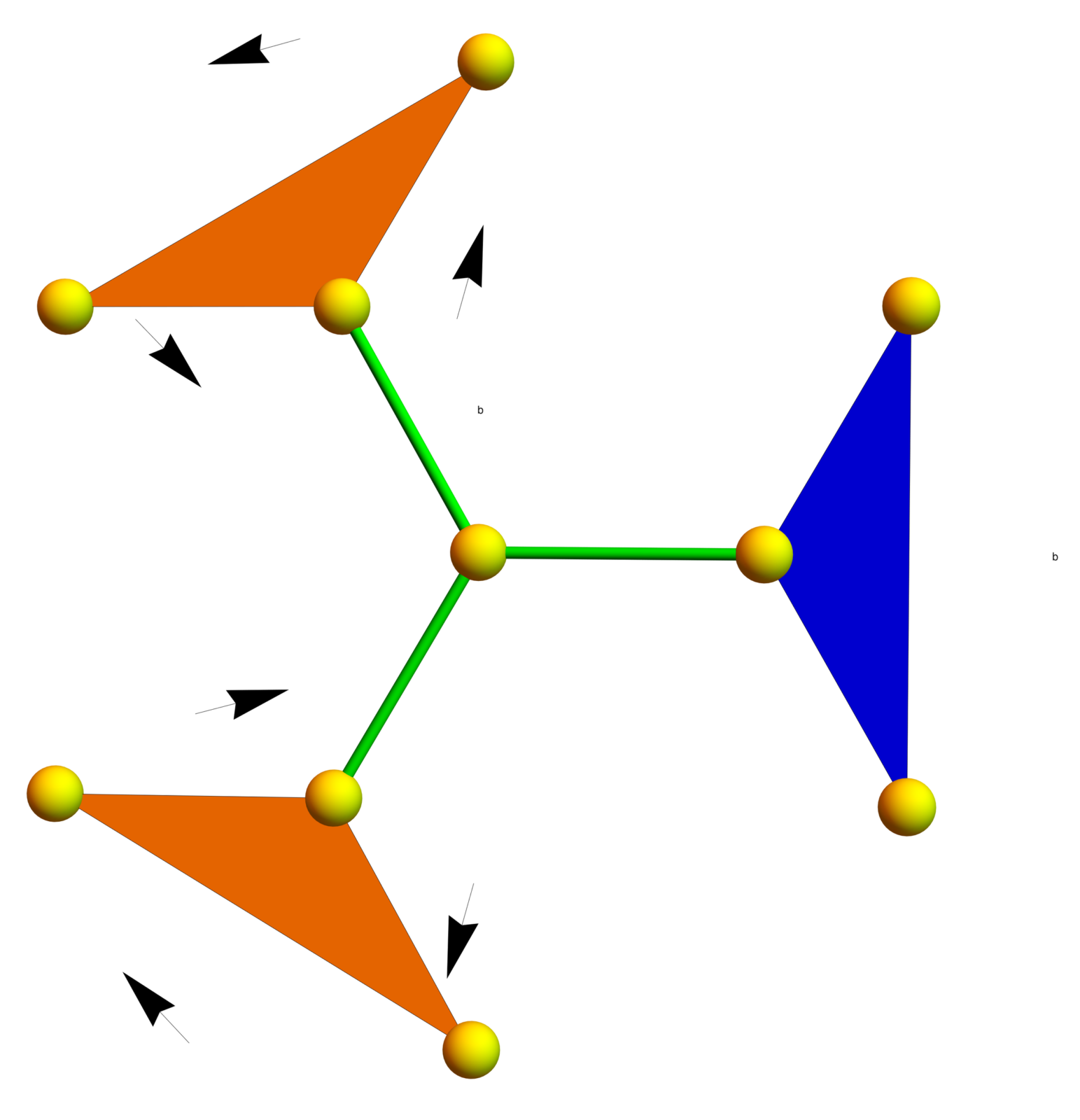
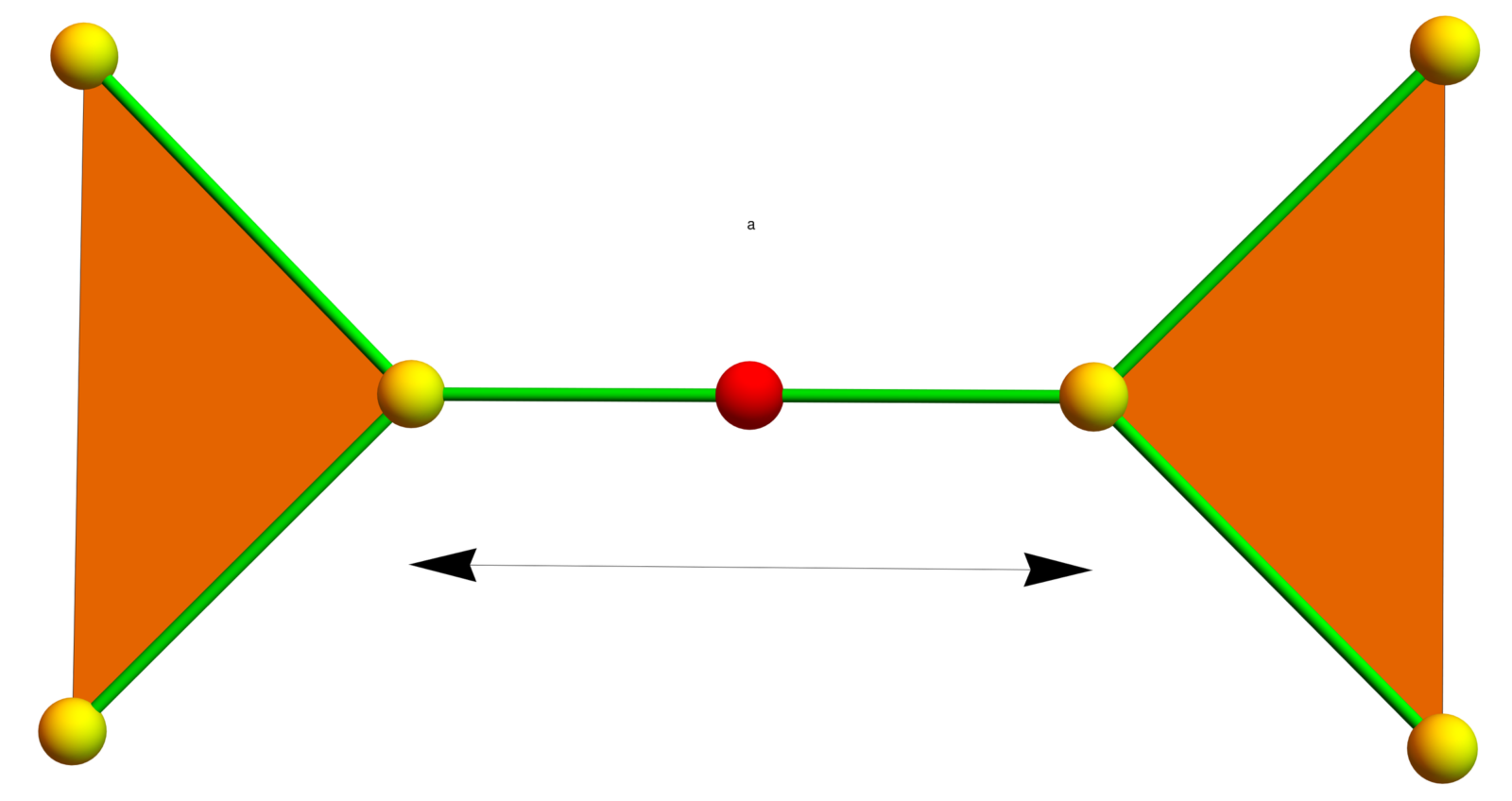
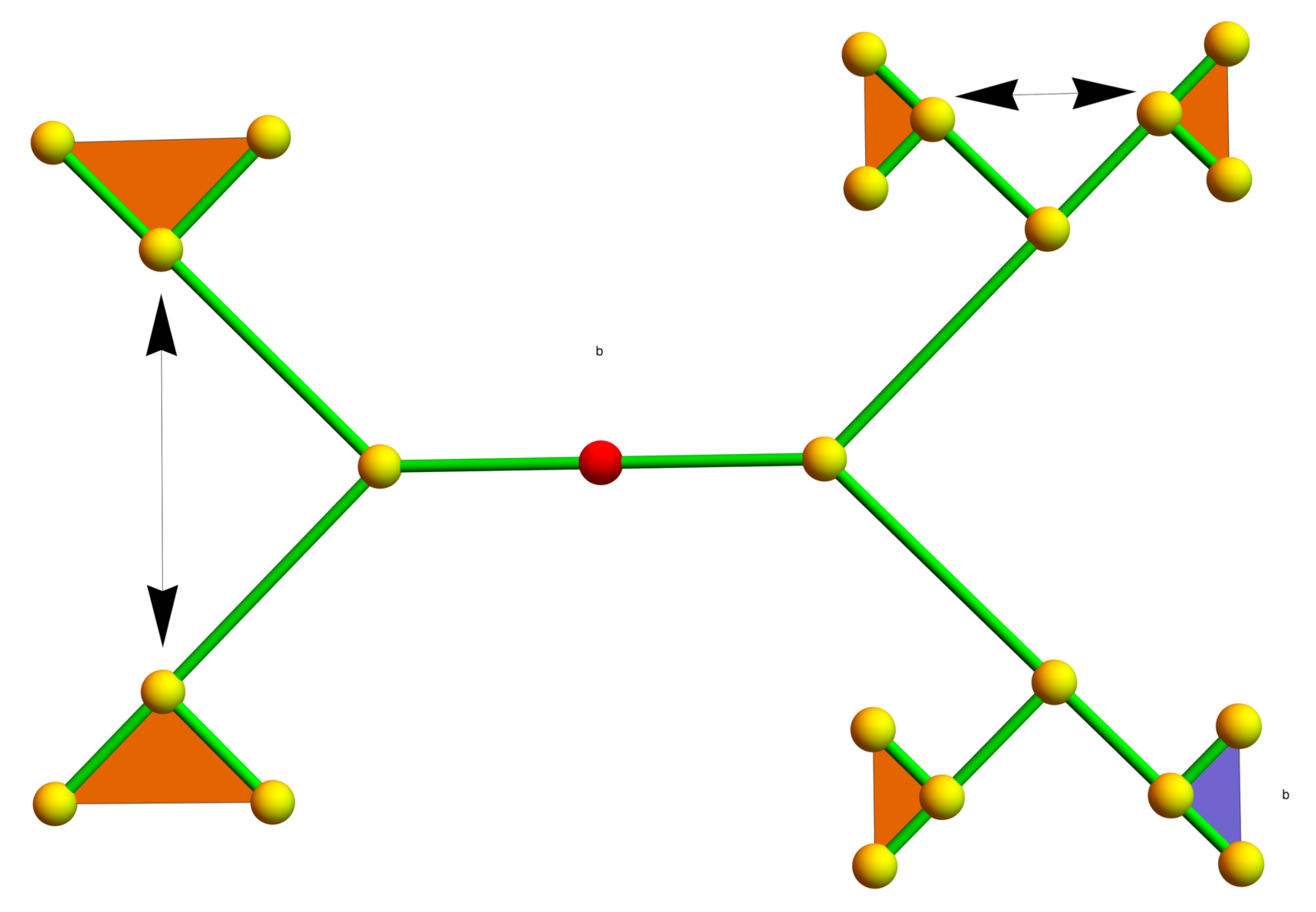
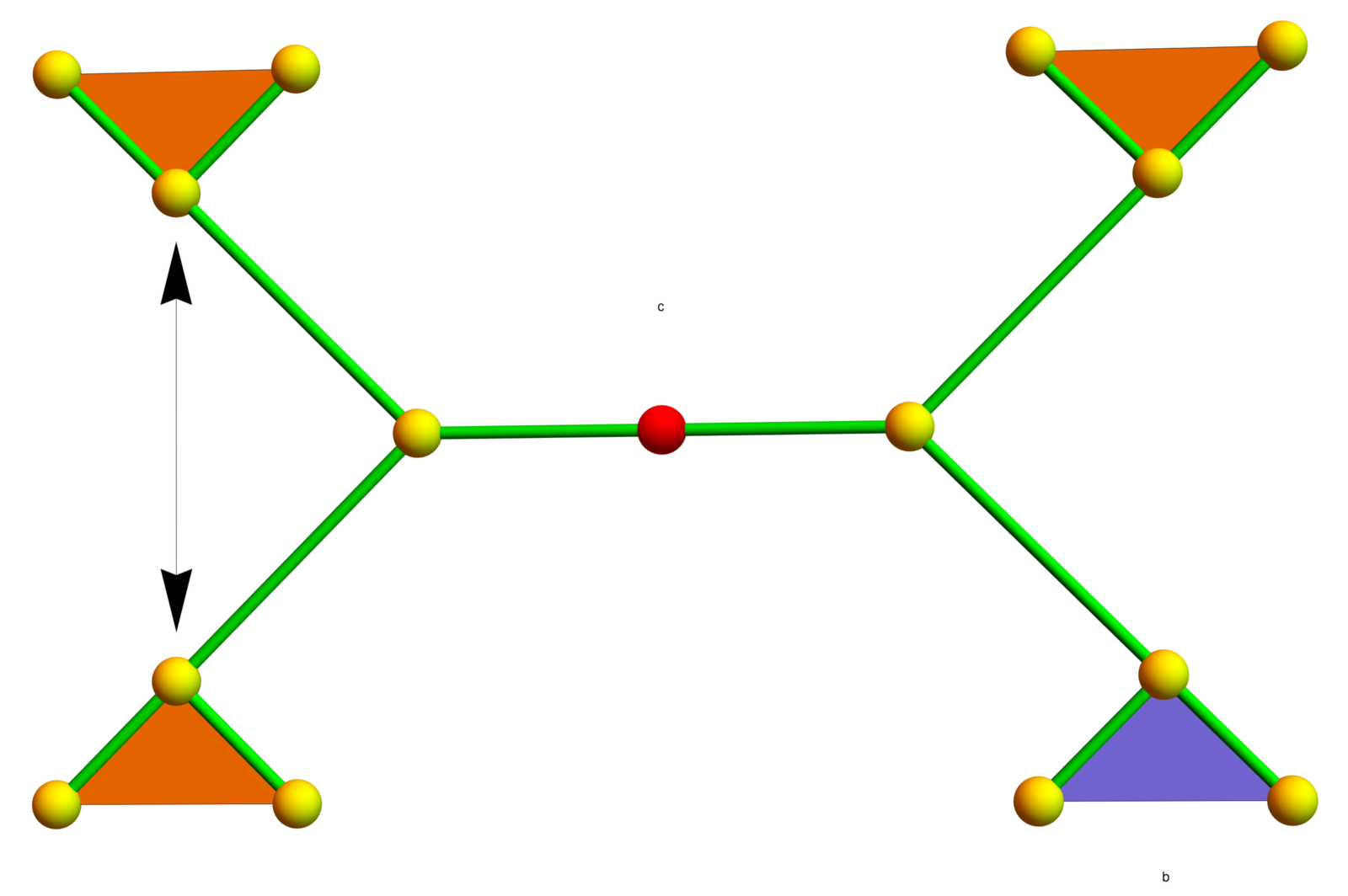
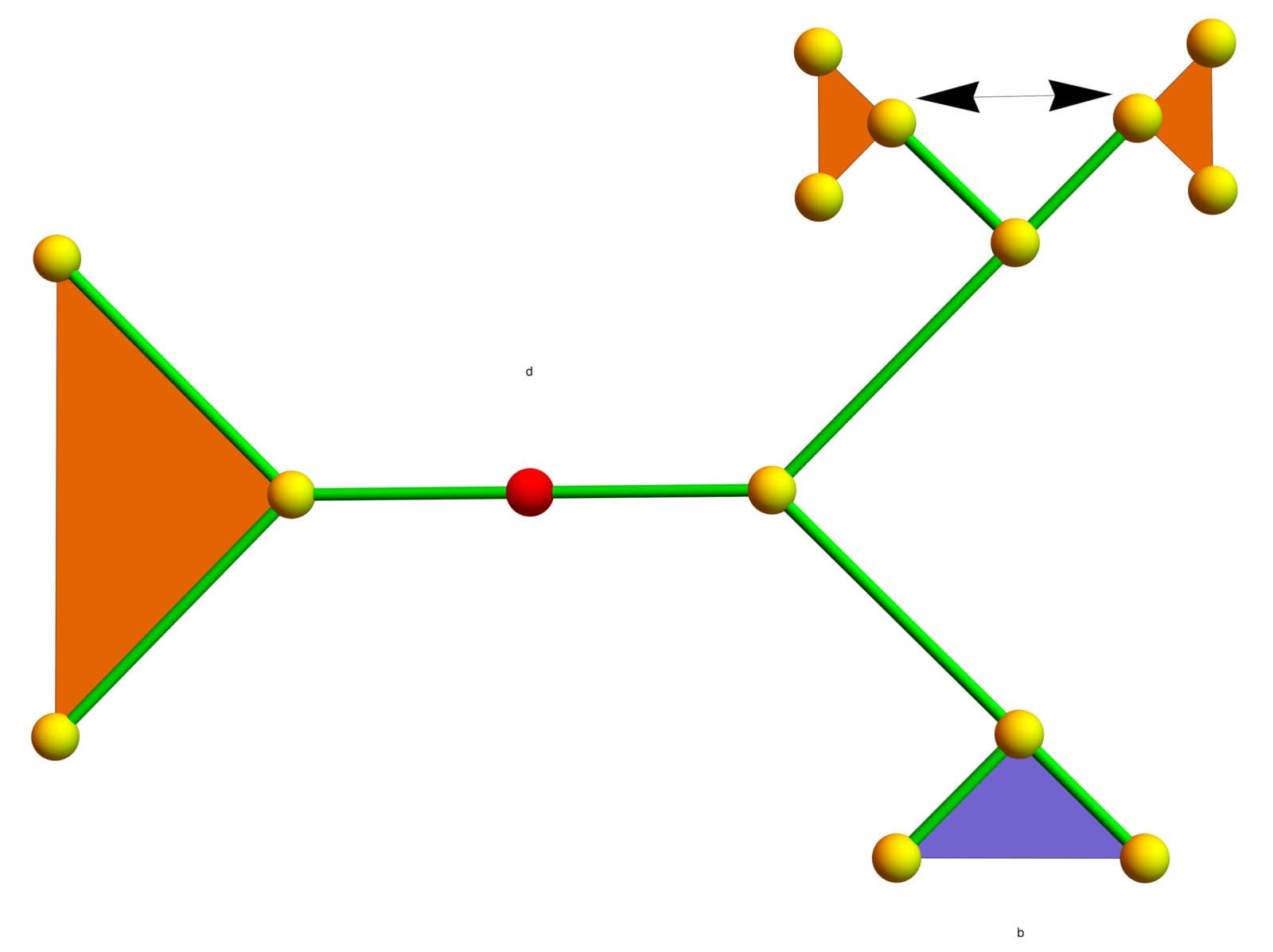
We look at the 2x2x2 Rubik cube group which is , the Grigorchuk group, a group with intermediate growth rate, as well as the Gupta-Sidki group, which is also a counter example to the weak Burnside problem but which is remarkable due to its simplicity. A few remarks and links to the video. I have worked in 1987 (unsuccessfully) to prove that the Gupta-Sidki group is not finitely presentable (a question of Baumslag posed when giving this course at ETH). Here are better pictures of the generators of the Gupta-Sidki group. In the second generator b, the action of b is recursively applied to the blue branch of the Bethe lattice. About the Rubik: Here is a document which shows my solution strategy I had developed and used in high school. It also contains a 2x2x2x2 cube.