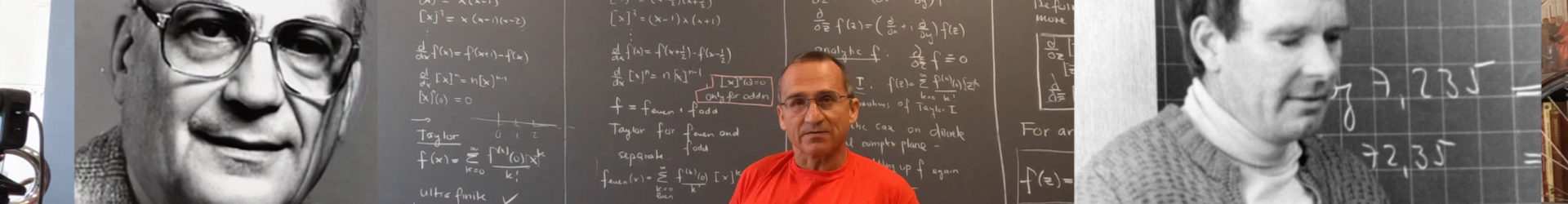Towards Ultra-Finite Taylor

An ultra-finite Taylor theorem is given by a basis of polynomials and a discrete derivative d/dx such that and as well as for every grid point with . For such a basis one has automatically a Taylor theorem and also has the ultra-finite property that for every x, the sum terminates after finitely many terms. This is important for an ultra-finitiest, who does not want accept limits or infinity. Such an algebra exists and my Pecha-Kucha talk from 2013 dealt with it. We just define and . The problem with this is that the ultra-finite property only holds for non-negative x. For negative x, the Taylor series does not necessarily terminate after finitely many steps.

After switching to the symmetric derivative , which still has a smallest step but is symmetric, the polynomial algebra is defined on the half integers (the Barycentric refinement). An ultra-finite set-up now requires to consider an expansion on even and odd parts of the function which corresponds some-how to distinguish parts on the integers (usual functions or 0-forms ) or half integers (the home of 1-forms). Now this is not so bad and works well but when moving to the complex we have to split up the complex up in four parts. When recording the following video, I had been hoping still that there is an ultra-finite symmetric Taylor algebra which does not require a split-up. At the moment (while writing this blog entry), I’m pretty sure that such an algebra actually does not exist for the symmetric derivative. I was looking for the algebra using linear algebra. We can still enforce by adding constants but not more. Again, we somehow are forced naturally to a half-integer situation with a dihedral set-up which requires to split up the Taylor result into a position and velocity. This led to excursions into natural spaces, (like natural metric spaces, natural groups or natural graphs) something I had pursued earlier. It is also quite natural from a graph theoretical view. Vertices and edges are different things. School calculus does not distinguish in single variable between 0-forms and 1-forms, leading to puzzles like why density integrals are orientation agnostic while the fundamental theorem of calculus is orientation aware or puzzles why the Lie derivative in one dimension is , where d is the exterior derivative and brings us back to 0-forms. One really only understand this when looking at Stokes theorem in arbitrary dimension or when learning differential geometry (Cartan’s magic formula for example). It is just that in the discrete one-dimensional quantum set-up, we can no more lie, as hard as we try to. The difference between geometric measure theory (which is a Fermionic calculus, dealing with things like differential forms, fields or currents) and integral geometry (which is a Bosonic calculus dealing with quantities like valuations, area or volume) becomes here apparent already in one dimensions.

By the way, the movie mentions Max Jeger (my geometry 1,2 and intro diff geometry prof at ETHZ) as well as Roland Staerk (my high school math teacher at the Kanti Schaffhausen for 5 years). Both are academic grand children of Heinz Hopf. Both had impeccable mathematical taste (I must say that I found Jeger’s geometry a bit too didactical at the time, but as a freshmen math student, one often is too arrogant). Interestingly, both Jeger and Staerk early on realized the importance of computers in math education. Not surprising is also that other children of Hopf like Eduard Stiefel were both mathematicians and computer scientists (at that time the fields were not yet separated). Jeger would bring often his Commodore computer to class and demonstrate something (programmed in Basic) and Staerk would give me and an other student (Christian Styger) the key to the school’s math library with the schools Olivetti computer (where we would program a few things, also in Basic of course).