What is geometry?

In the context of quantum calculus one is interested in discrete structures like graphs or finite abstract simplicial complexes studied primarily in combinatorics or combinatorial topology. Are they geometry? Are they calculus?

What is geometry?

In MathE320 I try to use the following definition:

The symmetry statement is borrows from Klein’s Erlangen program” which classifies geometries according to their symmetry. [Source of Klein’s manifest]. In order to have a “symmetry group”, there must be objects which are transformed like lines are mapped to lines in projective geometry. The definition of geometry given in Wikipedia like “relations between points, lines, surfaces, solids and higher dimensional analogues” hardly covers modern algebraic geometries (like ring theory) or fractal geometry (dealing with shapes of non-integer dimension) or geometric measure theory (part also of analysis and calculus) integral geometry (relating with probability theory), non-commutative geometry (much functional analysis and differential geometry). “Relations between points” is vague. One can interpret a “relation” as a symmetry. But if we look at the notion “points and their relations”, then this covers already all of mathematics because Cantor has based all of mathematics in the language of set theory. Also topology deals with shape and symmetry (continuous transformations) but much of topology is not concerned so much with size like length, area, often not even with dimension as a topological transformation can change the Hausdorff dimension of a shape. On the other hand, an abstract metric space (X,d) is clearly geometry as we are interested in objects in X, how they transform under isometries and have the isometry group acting on it. It is maybe pointless to argue about what the best definition of a subject is. Each mathematician should make one for him or herself. But let me explain why the three ingredients “Shape”, “Size” and “Symmetry” all appear to be important in geometry.

A definition should also honor the history and culture and the development of mathematics. In the past, one indeeds seemed have seen geometry much more limited. Descartes “La Geometry” (1638) dealt first with rather simple planimetric situations continuing somehow where Euclid left off. Also Hilbert in his “Grundlagen der Geometrie” from 1902 deals with an axiomatization of geometry dealing with lines, planes, polygons, complex numbers, proportions, projective geometry and non-Eulidean geometry. He would however not see Riemannian geometry as geometry as we do today, or the geometry inherent in group theory or abstract algebra. So, when looking at the term historically it is true that geometry was used in a rather limited way.

Since history also include the more recent history and so modern mathematics it is necessary to expand the scope of geometry. This is tricky as
the classification of mathematicsal structures is not a “partition”, it is a “covering”. There is much overlap between algebra and geometry (as Descartes already showed us) and there is geometry in Hilbert spaces (as Hilbert has shown). There is geometry in virtually all parts of mathematics.

Shapes The earliest geometries dealt with triangles, squares (clay tablets), trapezoids and circles (Rhind papyrus 1600 BC). Much of geometry until Euclid dealt with these shapes. The Greeks added Platonic solids and spheres. Today, we look at a larger class of “shapes”. Examples: we work with algebraic varieties, or parametrized spaces given in calculus as a map . Varieties have been been generalized to Schemes, Surfaces have been generalized to Manifolds. Schemes appear very general but they have even be generalized to larger objects like Algebraic Stacks. Manifolds have been generalized to Orbifolds.

Size: Volume and area have been computed early on. In Babylonian mathematics one has already estimated the circumference of a circle as 3 and known the volume of a cylinder. The Babylonians had not yet the formula for the volume of the frustrum. This was established by the Egyptians (Moscow Papyrus). The Greeks continued to look for areas and volumes. It was Archimedes who established both: found a formula for the area of a disk and the volume of the spheres. The Greeks also introduced angles. The notion of “size” has been generalized vastly. In Riemannian geometry arc-length and distances heavily rely on the differential geometric notions. New notions between length, area and volume have been introduced in the form of Hausdorff measure. Size can also be measured by more topological concepts like Euler characteristic. One can see measure theory and in particular probability theory as a theory which particularly strongly focuses on a notion of size in the form of “probability”.

Symmetry: The importance of symmetry appears have been realized first by the Greeks who looked at equilateral triangles. Similar triangles (the symmetry group being the group of Euclidean transformations like rotations, translations and reflections). But they also went to higher dimensions and introduced Platonic solids. Some shapes with symmetries of the Platonic solids appeared in the form of Carved Stone balls for which the oldest known are from 3200 BC but if one looks at those examples, they are confined to the symmetry of the cube or maybe the tetrahedron. The Platonic solids came with the ancient Greeks. It was Theaetetus who first described the list of all 5 Platonic solids. It took much longer until the notion of symmetry group was appreciated. Since Klein’s Erlangen program, the symemtry group is the gold standard for classifying geometries.

Moscow Papyrus

Rhind Papyrus

Unfortunately, even the Brittish museum has only small scanned versions online. I still look for high resulution pictures of these papyri. Here are the largest resolutions I could find on that museum site:

Simplicial complexes as a geometry

Lets look at an example of a geometry, he geometry of simplicial complexes. The definition of this geometry could not be simpler: it is a finite set of non-empty subsets which is closed under the operation of taking finite non-empty subsets. It is amazing what mathematical notions go over to this simple structure. We can look at “level surfaces”, have notions of “spheres” and “lines” and “geodesics”, have “curvature” and “indices”. There is is hardly any part of mathematics we know in “geometry” what can not be realized in this simple frame work. One can even try Atiyah Singer type results which appears outragious. But I’m convinced that if it is preposterous, then its only due to my own limitations. It should be possible in the future to capture all the esssential parts of these theorems. One of the test grounds will be Hirzebruch-Riemann-Roch in the discrete, generalizing the Baker-Norine Riemann Roch but which can be seen in the frame work of Atiyah-Singer.

The shapes : Lets assume a simplicial complex is a background geometry. The vertices are the zero dimensional simplices, the line segments are the one dimensional simplices, etc. One can now look at more general objects. A closed curve for example is a subcomplex for which every unit sphere is a zero dimensional complex with two points. A two dimensional surface is a complex for which every unit sphere is a closed curve.

The size : The f-vector of a simplicial complex G is the vector , where is the number of elements in G with elements. For any shape inside a given complex one can look at its f-vector. Each of the entries is what one calls a valuation. The Kruskal-Katona theorem gives a necessary and sufficient condition for an f-vector to come from a simplicial complex.

The symmetries : A transformation on a complex belongs to the symmetry group of the geometry if it maps simplicial complexes to simplicial complexes and it if has an inverse which does the same. If the background complex is regular like a periodic lattice (discrete torus), there are discrete symmetries. The symmetry group is not as rich as in the continuum. But there can be ways around it, especially if one also allows scaling symmetries in the form of Barycentric refinements.

An example: the homology 3-sphere

The homology 3-sphere is a 3-manifold which has the same homology than the 3-sphere but which is not homeomorphic to the 3-sphere. It is obtained by taking a solid dodecahedron, in which the opposite face pentagons are identitifed. It has the orbifold discription SO(3)/Icosahedralgroup but it is a nice smooth 3-manifold. One way to compute with this in a finite manner is to build a triangulation which is a graph, then build the Whitney complex.

We need to start with a simplicial complex. A small complex has been given by Anders Bjoerner and Frank Lutz in 2000. It is a finite set G of non-empty sets given below (the number of sets is 392). The F-vector of this complex is (16, 106, 180, 90) and we see the Euler characteristic is v-e+f-c = 16-106+180-90 = 0, where v is the number of points, e the number of line segements, f the number of surface elements and c the number of space components. It is a general fact in topology (a consequence of Poincare duality, or vanishing of curvature due to Dehn-Sommerville) which assures that the Euler characteristic of a 3-manifold is zero. Now this appears just to be an example of a 3-manifold, what is so special about it? The point is that it has the same cohomology than the 3-sphere but that it is not homeomorphic to it. It also can help to the excitement that some cosmologists once have speculated (based on some data from the microwave background radiation pictures) maybe 15 years ago that the space part of our universe could be a homology sphere. Here is the set of sets:

G={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{1,2},{1,3},{1,4},{1,5},{1,6},{1,7},{1,8},{1,9},{1,10},{1,11},{1,12},{1,13},{1,14},{1,15},{2,3},{2,4},{2,5},{2,6},{2,7},{2,8},{2,9},{2,10},{2,11},{2,12},{2,13},{2,14},{2,15},{3,4},{3,5},{3,7},{3,10},{3,11},{3,12},{3,13},{3,14},{3,15},{4,5},{4,6},{4,7},{4,8},{4,9},{4,10},{4,11},{4,12},{4,13},{4,14},{4,15},{5,6},{5,7},{5,8},{5,9},{5,10},{5,11},{5,12},{5,13},{5,14},{5,15},{6,7},{6,10},{6,11},{6,12},{6,13},{6,14},{6,15},{7,8},{7,9},{7,10},{7,11},{7,12},{7,13},{7,14},{7,15},{8,9},{8,10},{8,11},{8,12},{8,13},{8,14},{8,15},{9,10},{9,11},{9,12},{9,13},{9,14},{9,15},{9,16},{10,11},{10,12},{10,13},{10,14},{10,15},{10,16},{11,12},{11,13},{11,14},{11,15},{11,16},{12,13},{12,14},{12,15},{13,14},{13,15},{13,16},{14,15},{14,16},{15,16},{1,2,4},{1,2,6},{1,2,9},{1,2,14},{1,2,15},{1,3,4},{1,3,7},{1,3,10},{1,3,12},{1,3,15},{1,4,9},{1,4,12},{1,4,15},{1,5,6},{1,5,8},{1,5,11},{1,5,13},{1,5,14},{1,6,13},{1,6,14},{1,6,15},{1,7,8},{1,7,10},{1,7,11},{1,7,12},{1,8,10},{1,8,11},{1,8,13},{1,9,11},{1,9,12},{1,9,14},{1,10,13},{1,10,15},{1,11,12},{1,11,14},{1,13,15},{2,3,5},{2,3,7},{2,3,10},{2,3,11},{2,3,13},{2,4,9},{2,4,11},{2,4,13},{2,4,15},{2,5,8},{2,5,10},{2,5,11},{2,5,12},{2,6,10},{2,6,12},{2,6,14},{2,6,15},{2,7,9},{2,7,10},{2,7,13},{2,7,14},{2,8,11},{2,8,12},{2,8,15},{2,9,13},{2,9,14},{2,10,12},{2,10,14},{2,11,13},{2,11,15},{2,12,15},{3,4,5},{3,4,12},{3,4,14},{3,4,15},{3,5,10},{3,5,11},{3,5,14},{3,5,15},{3,7,10},{3,7,12},{3,7,13},{3,10,15},{3,11,13},{3,11,14},{3,12,13},{3,12,14},{3,13,14},{4,5,6},{4,5,7},{4,5,14},{4,5,15},{4,6,7},{4,6,10},{4,6,11},{4,6,14},{4,7,11},{4,7,15},{4,8,9},{4,8,10},{4,8,12},{4,8,13},{4,8,14},{4,9,12},{4,9,13},{4,10,11},{4,10,13},{4,10,14},{4,11,13},{4,11,15},{4,12,14},{5,6,7},{5,6,13},{5,6,14},{5,7,9},{5,7,13},{5,7,15},{5,8,9},{5,8,11},{5,8,12},{5,8,13},{5,9,10},{5,9,12},{5,9,13},{5,9,15},{5,10,12},{5,10,15},{5,11,14},{6,7,11},{6,7,12},{6,7,13},{6,10,11},{6,10,12},{6,10,14},{6,11,12},{6,12,13},{6,12,15},{6,13,15},{7,8,10},{7,8,11},{7,8,14},{7,8,15},{7,9,13},{7,9,14},{7,9,15},{7,10,14},{7,11,12},{7,11,15},{7,12,13},{7,14,15},{8,9,12},{8,9,13},{8,10,13},{8,10,14},{8,11,15},{8,12,14},{8,12,15},{8,14,15},{9,10,11},{9,10,12},{9,10,15},{9,10,16},{9,11,12},{9,11,14},{9,11,16},{9,14,15},{9,14,16},{9,15,16},{10,11,12},{10,11,13},{10,11,16},{10,13,15},{10,13,16},{10,15,16},{11,13,14},{11,13,16},{11,14,16},{12,13,14},{12,13,15},{12,14,15},{13,14,15},{13,14,16},{13,15,16},{14,15,16},{1,2,4,9},{1,2,4,15},{1,2,6,14},{1,2,6,15},{1,2,9,14},{1,3,4,12},{1,3,4,15},{1,3,7,10},{1,3,7,12},{1,3,10,15},{1,4,9,12},{1,5,6,13},{1,5,6,14},{1,5,8,11},{1,5,8,13},{1,5,11,14},{1,6,13,15},{1,7,8,10},{1,7,8,11},{1,7,11,12},{1,8,10,13},{1,9,11,12},{1,9,11,14},{1,10,13,15},{2,3,5,10},{2,3,5,11},{2,3,7,10},{2,3,7,13},{2,3,11,13},{2,4,9,13},{2,4,11,13},{2,4,11,15},{2,5,8,11},{2,5,8,12},{2,5,10,12},{2,6,10,12},{2,6,10,14},{2,6,12,15},{2,7,9,13},{2,7,9,14},{2,7,10,14},{2,8,11,15},{2,8,12,15},{3,4,5,14},{3,4,5,15},{3,4,12,14},{3,5,10,15},{3,5,11,14},{3,7,12,13},{3,11,13,14},{3,12,13,14},{4,5,6,7},{4,5,6,14},{4,5,7,15},{4,6,7,11},{4,6,10,11},{4,6,10,14},{4,7,11,15},{4,8,9,12},{4,8,9,13},{4,8,10,13},{4,8,10,14},{4,8,12,14},{4,10,11,13},{5,6,7,13},{5,7,9,13},{5,7,9,15},{5,8,9,12},{5,8,9,13},{5,9,10,12},{5,9,10,15},{6,7,11,12},{6,7,12,13},{6,10,11,12},{6,12,13,15},{7,8,10,14},{7,8,11,15},{7,8,14,15},{7,9,14,15},{8,12,14,15},{9,10,11,12},{9,10,11,16},{9,10,15,16},{9,11,14,16},{9,14,15,16},{10,11,13,16},{10,13,15,16},{11,13,14,16},{12,13,14,15},{13,14,15,16}}

These sets are simple but its not that we see much structure by staring at these sets. Thats why I use graphs to do geometry which carry natural simplicial complexes, annoying every graph theorists because virtually every graph theory book from the 20th century treats graphs as one dimensional simplicial complexes. Graphs allow better visualization. Granted, if we draw the graph belonging to a homology sphere, it also does not give much insight (the graph is seen to the right). Still, it is easier to think about it geometrically.

As pointed out in the next movie at around 3:15, one would only need 135 refinement steps to get from such a complex to a complex in which every Planck volume of the visible universe is covered by a 3-simplex:

The Cohomology of the complex can be computed easily with a few lines of code. Just find the Dirac matrix D, then form the Hodge matrix L=D² then find the kernel of the blocks. Here are the two 393×393 matrices:

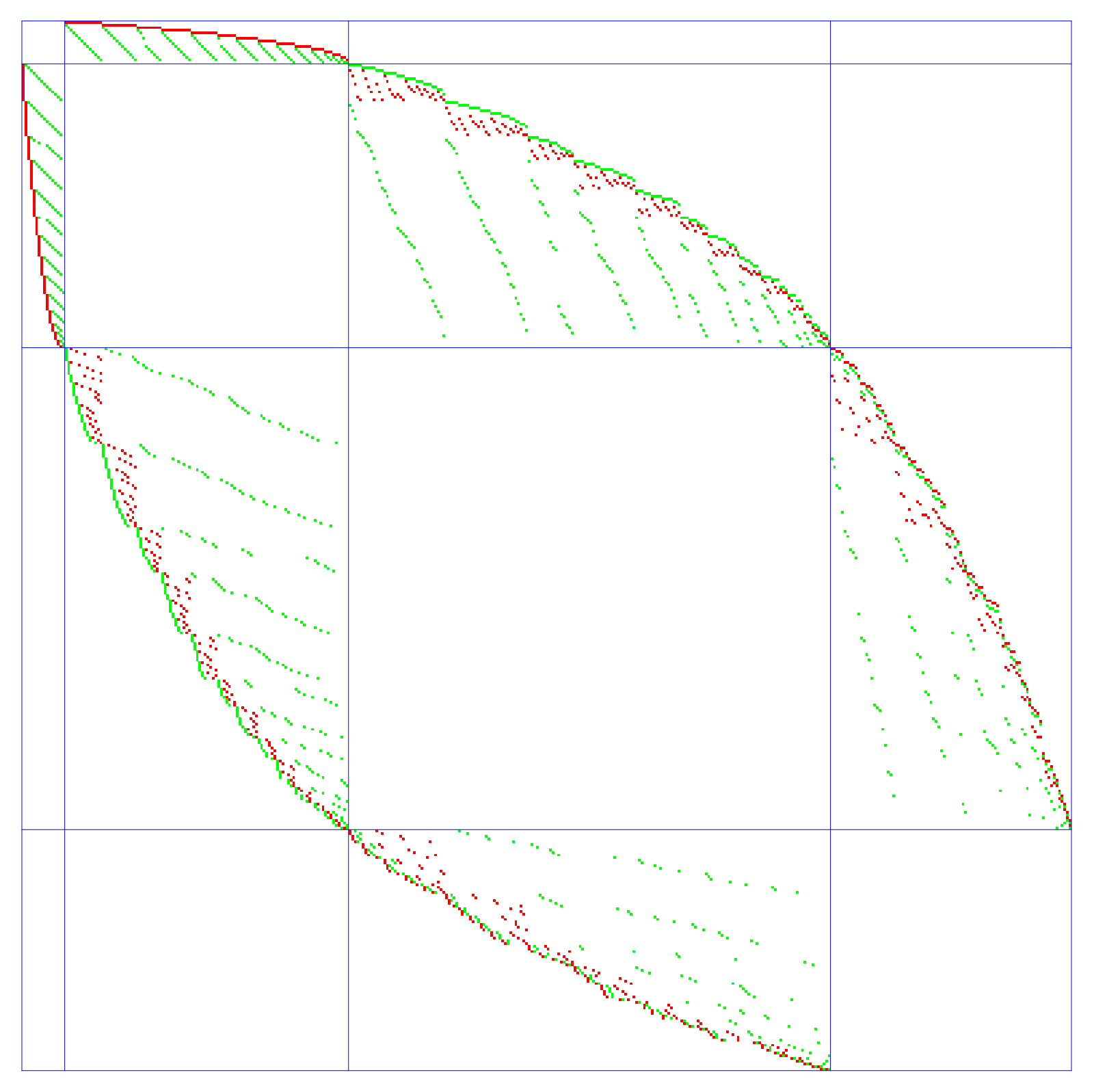
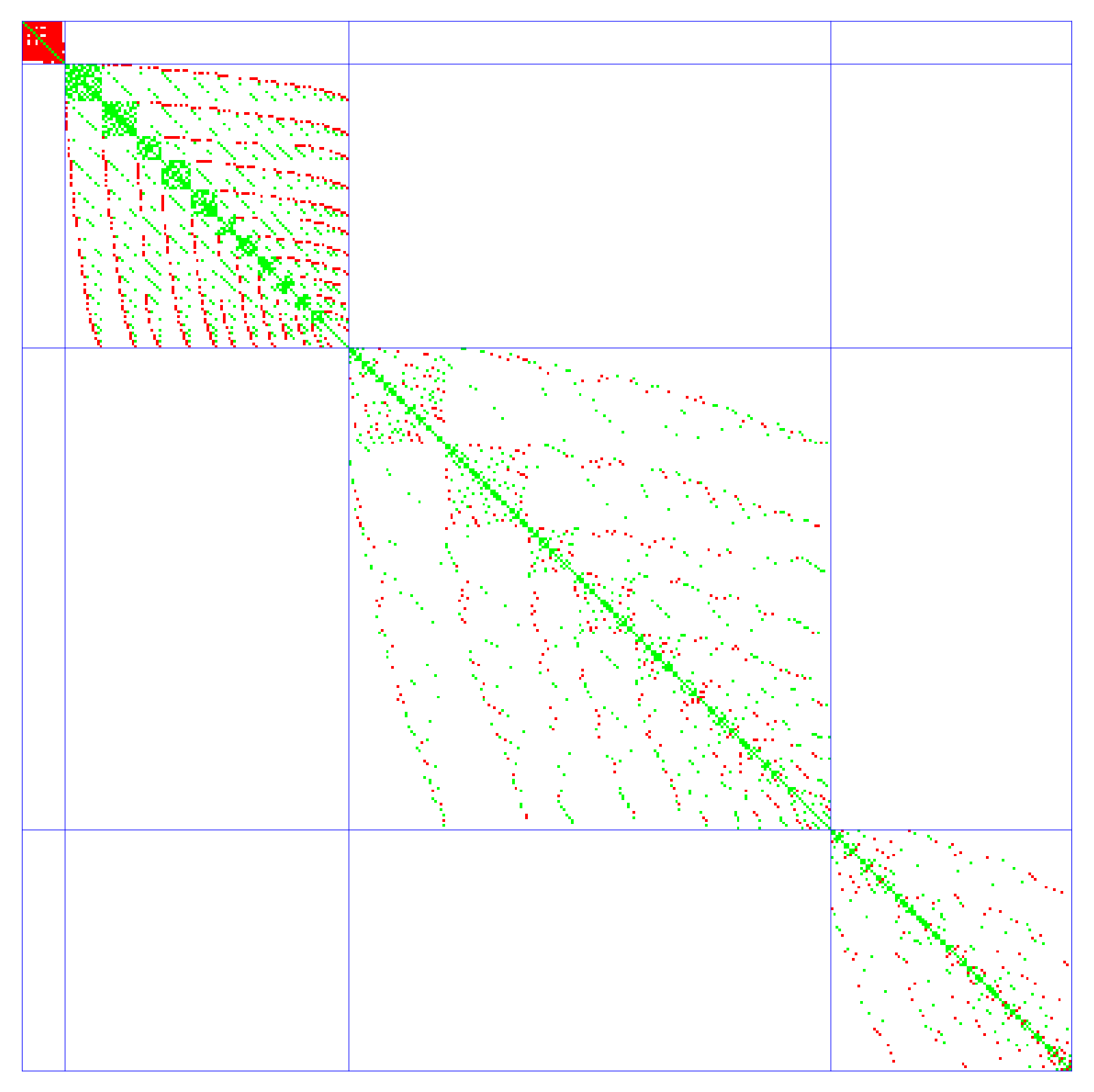
Computing the nullety, we see that the Betti vector is (1,0,0,1) as it should be.

Anyway, I hope this post should show that the simplest axiom system known in mathematics, the structure of a simplicial complex with 1 Axiom (!) has a richness which allows (using a half a dozen lines of mathmatica code) to compute from scratch the cohomology of a poincare cohomology sphere. It should definitely be included in “geometry:. The complexity of all the math involved is smaller than the complexity in setting up Euclids axioms. Yes, there is some computational complexity involved as we would have to row reduce a 392 x 392 matrix if we wanted to compute the cohomology classes by hand. Still, already Poincare has managated to compute the cohomology without computers. We today just have to type “NullSpace[A]” to get a basis for the cohomology groups. Anyway, the math behind computing the cohomology requires 3 weeks of linear algebra training only and no understanding of limits is required. It is all calculus without limits.