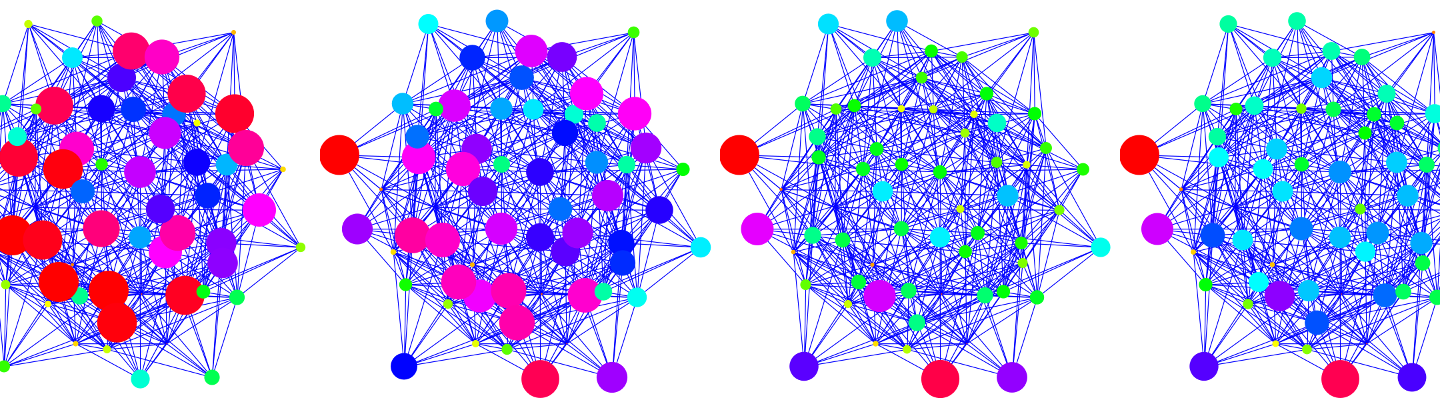
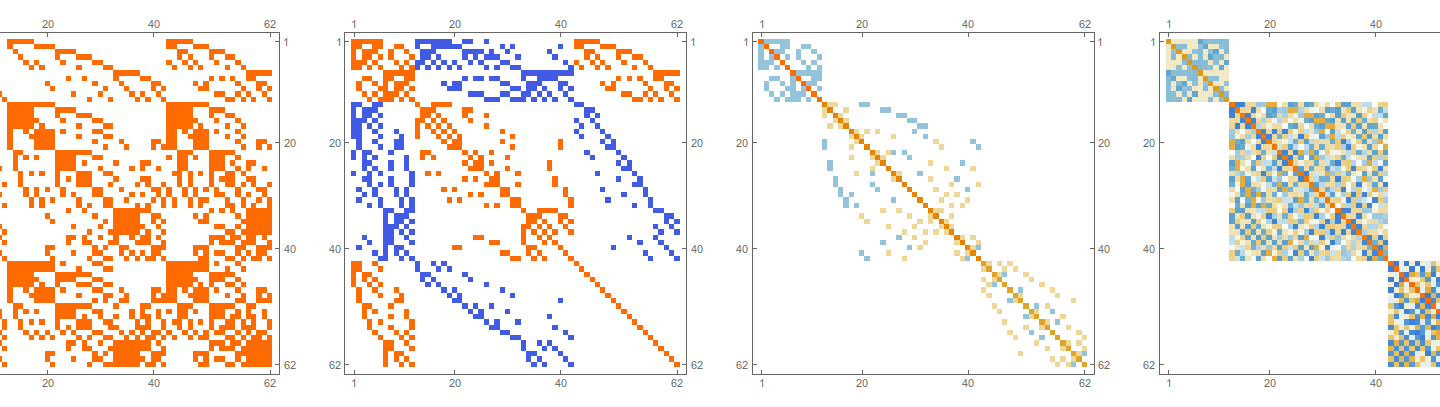
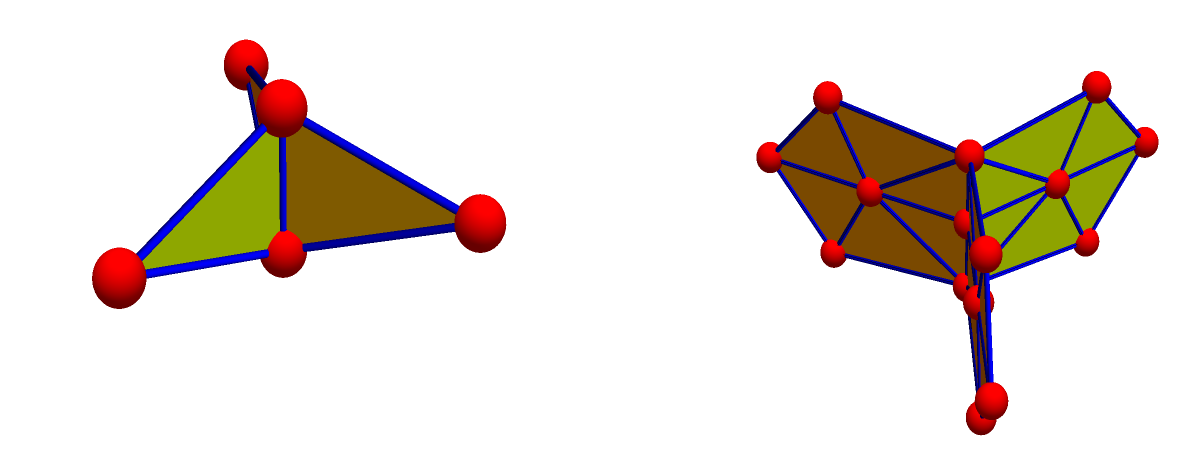
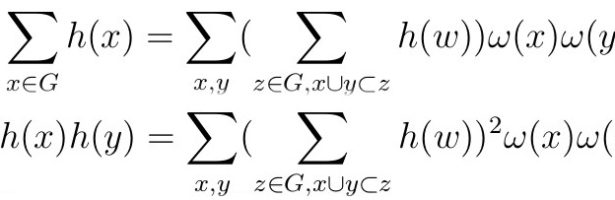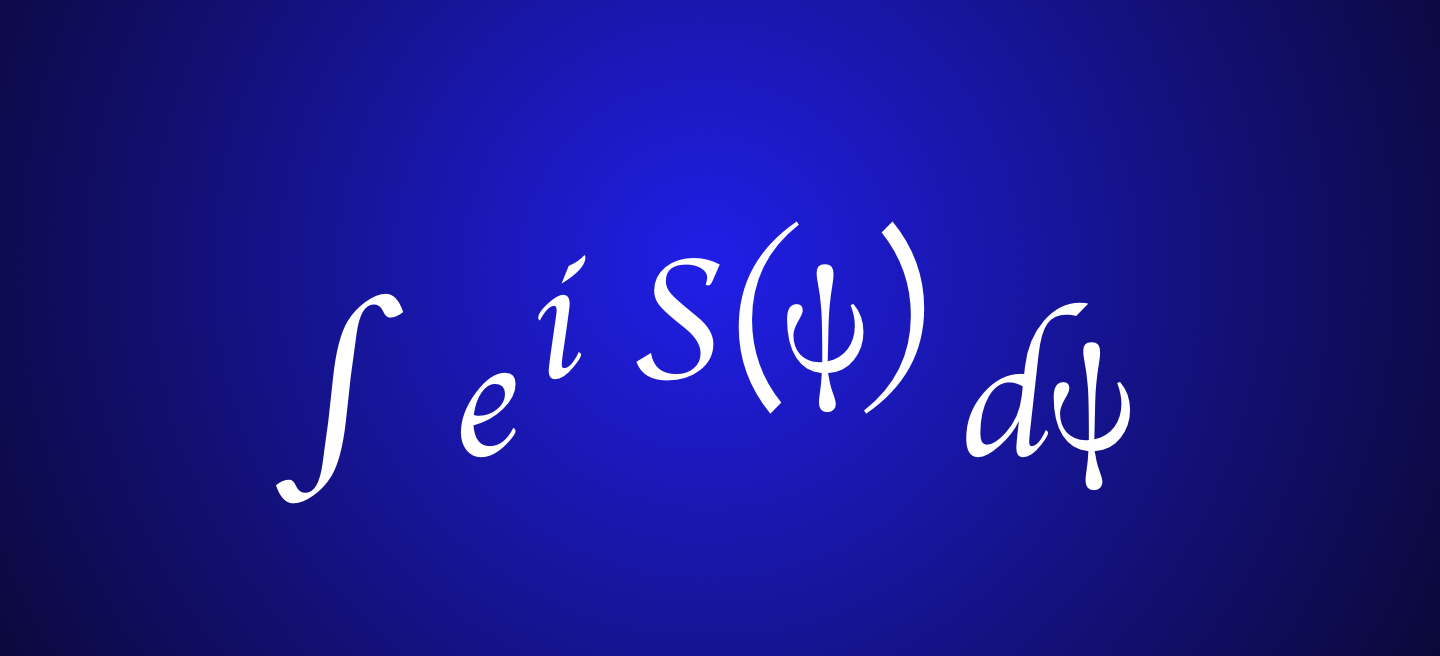Updates on QR and Curvature
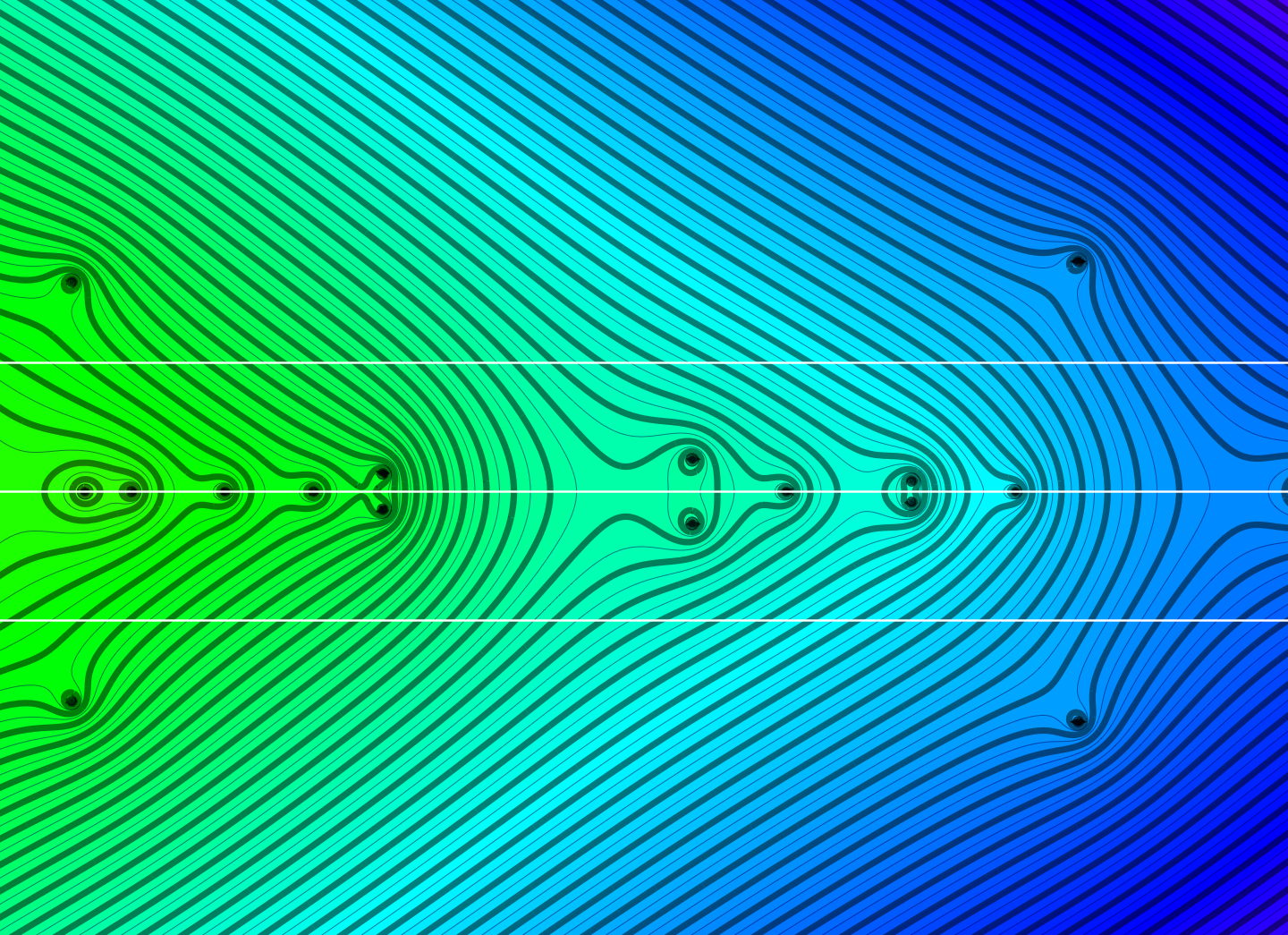
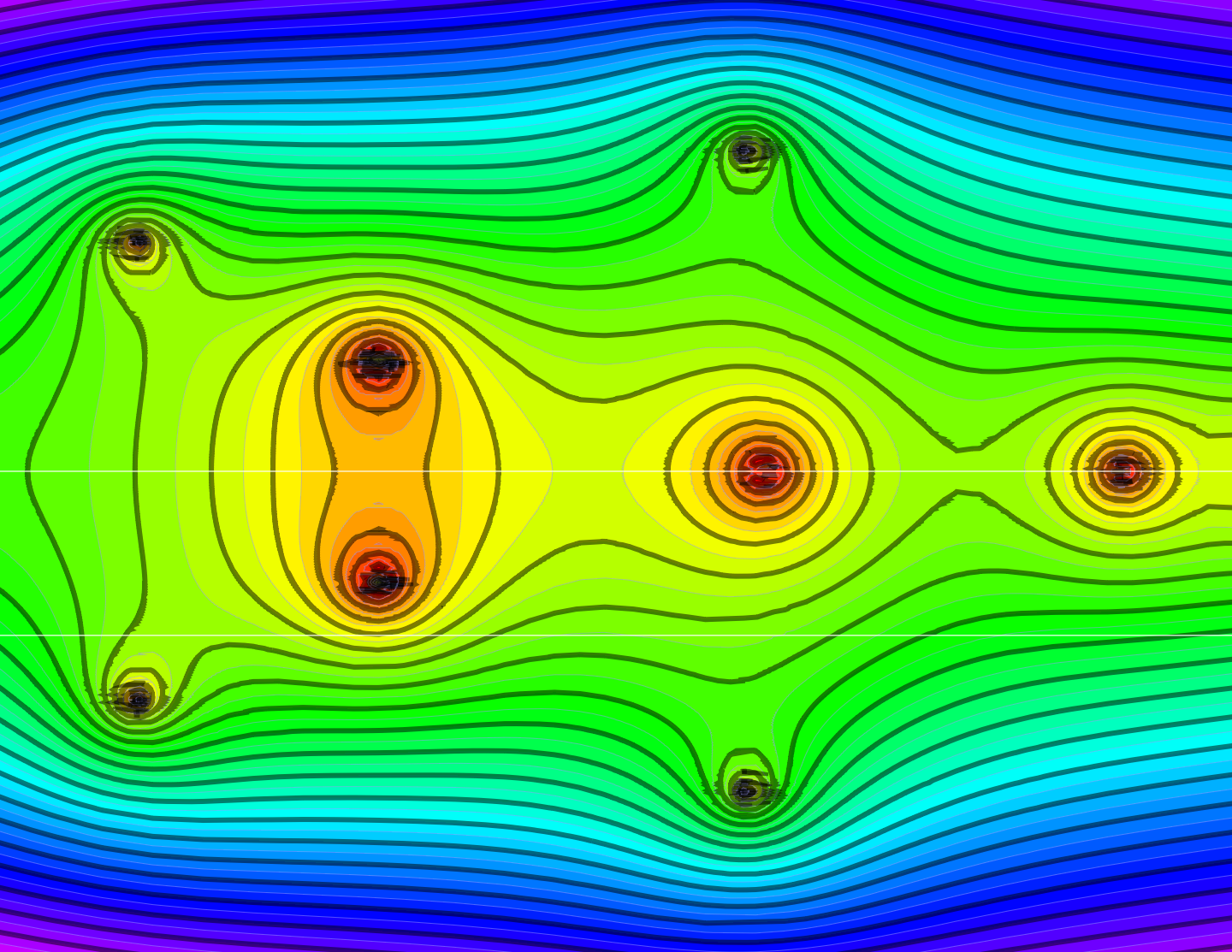
This is just an update on two topics looked over during the summer. In the case of the QR flow and Toda flow equivalence, I have had a hard time finding it due to some strange ways how Mathematica computes the QR composition. You can try yourself: the diagonal entries …